投稿日:2021年12月10日

部品の強度評価には、大きく分けて「静強度」と「疲労強度」があります。
静強度は材料や形状によって決まる「許容値」に対する「負荷荷重(応力)」の評価であるため、計算も単純で比較的分かりやすいのに比べ、疲労強度は「許容値」以外にも「応力集中」や「繰り返し回数」を考慮する必要があり、強度評価初心者の方には若干複雑です。
このコラムでは、金属における疲労破壊の基礎と、疲労強度の評価の流れを紹介します。
強度評価初心者の方で、疲労破壊の概念を勉強したい方はぜひ参考にしてください。
疲労破壊とは?
【疲労破壊現象】
疲労破壊は、「部品が繰り返し応力(引張)を受けることで、引張強度以下の応力負荷状態で生じる破壊現象」です。
静強度の定義では、弾性変形の範囲内であれば、荷重を除荷すると変形は元に戻るとされています。
しかし、これは人間の目で見える巨視的な範囲での定義であり、原子レベルの微視的な観点では、弾性変形範囲内でも一部の原子は元の位置に戻らない「非弾性的」なふるまいである「転位現象」を起こします。

疲労破壊は、この転位現象が繰り返すことで材料にダメージが蓄積していき、遂には破壊してしまう現象です。
疲労破壊は金属だけでなく、樹脂やプラスチック、ガラスなどでも発生します。
また、部品が加熱と冷却を繰り返し受けることで発生する「熱疲労」や、接触部品のすべりによって発生する「フレッチング疲労」など、特殊な疲労破壊現象があります。
損傷許容設計
疲労破壊を考慮すると部品が重くなりますが、航空機や原子炉などのように、重量、コスト、安全性などの制約で、十分な疲労強度を持てない部品もあります。
この様な部品は、繰り返し応力がかかる運用中に、検出できない初期き裂が発生し進展していくことを前提として部品寿命を評価する「損傷許容設計」が用いられます。
損傷許容設計は部品の交換を前提としており、下図のようにき裂がある程度進展しても、部品が持つ強度(残存強度)が繰り返し応力を上回るように、部品の交換期間を設定します。
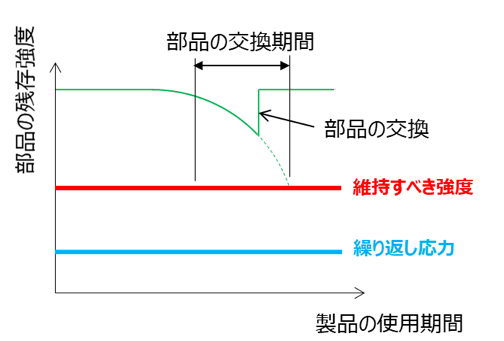
部品の寿命が短くて良い分、疲労破壊の繰り返し回数が小さくなるため、繰り返し応力が大きくなっても疲労強度が満足できるようになります。
損傷許容設計は疲労強度の評価概念とは全く異なったものですが、航空機の設計者は疲労強度設計と併せて覚えておきましょう。
①材料許容値
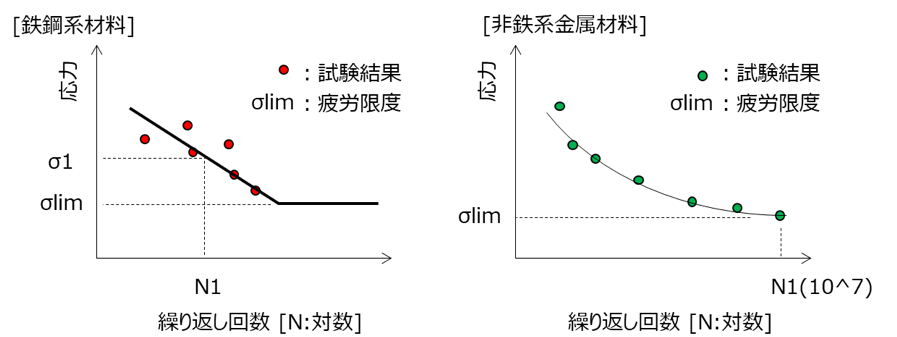
材料の疲労特性の評価には、縦軸に応力、横軸に繰り返し回数を示したS-N曲線が用いられます。
横軸の繰り返し回数は対数で表します。
S-N曲線は、鉄鋼系材料と非鉄系金属材料で疲労特性が異なります。
下図のように、鉄鋼系材料では、ある繰り返し応力:σlim以下の応力では疲労破壊が起こらず、直線となる領域が存在します。この時のσlimを疲労限度といいます。
これに対して、アルミなどの非鉄系金属材料には明確な疲労限度はありません。
航空機などの場合では、最大運用回数である107回の時の応力値を疲労限度とするのが一般的です。
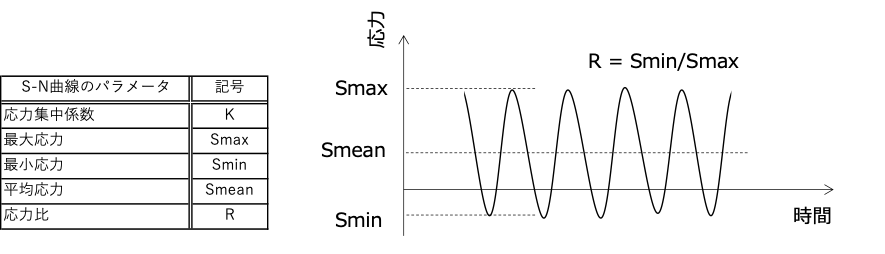
S-N曲線は疲労試験のデータから引いた線であり、以下のような細かい条件が決められています。
設計初心者の方は、間違った定義をしていないかを確認しましょう。
②応力集中
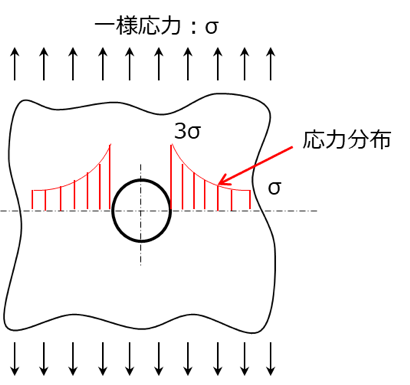
部品の断面形状が急変する場所では局所的な応力の増大現象が生じますが、これを応力集中といいます。
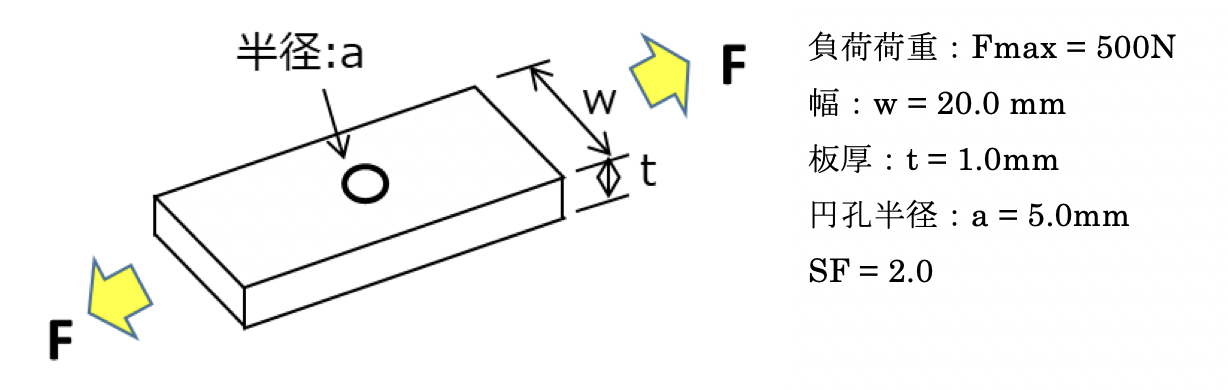
下図に、一様に引張応力が働く無限平板の、円孔周辺の応力状態を示します。
この時の応力の増加率を示す応力集中係数:Kは、3.0です。
疲労破壊は応力集中が発生する箇所で起きるため、応力集中がどのような場合に起きるかを把握することは設計者には非常に重要です。
応力集中係数は部品の形状だけでなく、荷重の負荷方法(曲げ、ねじり、引張)でも異なるため、注意が必要です。
なお、金属材料のような延性材料の静強度評価には、応力集中は考慮しません。
なぜなら延性材料が破壊する際には応力集中箇所から順に塑性変形していくため、塑性変形部から荷重を取れなくなり、結果的に破壊時の応力分布が均一となるからです。
逆に塑性変形しない脆性材料は、静強度でも応力集中を考慮する必要があります。
③疲労寿命を計算してみよう
では、実際の値を用いて疲労寿命を計算してみましょう。
なお本章で用いる計算は、簡略化のため以下を前提としています。
- 疲労限度以上の応力が発生するのは、製品の1使用ごとに1回のみ
- 発生する応力値は、毎回同じ値
【計算条件】
・以下の平板に、荷重Fが107回発生する時の疲労強度を求める。疲労強度の安全率である、SF(スキャッタファクタ)= 2.0とする。
【応力集中係数:K】
応力集中係数:Kを算出する。平板に一様な応力が働く時の応力集中係数は以下で算出される。
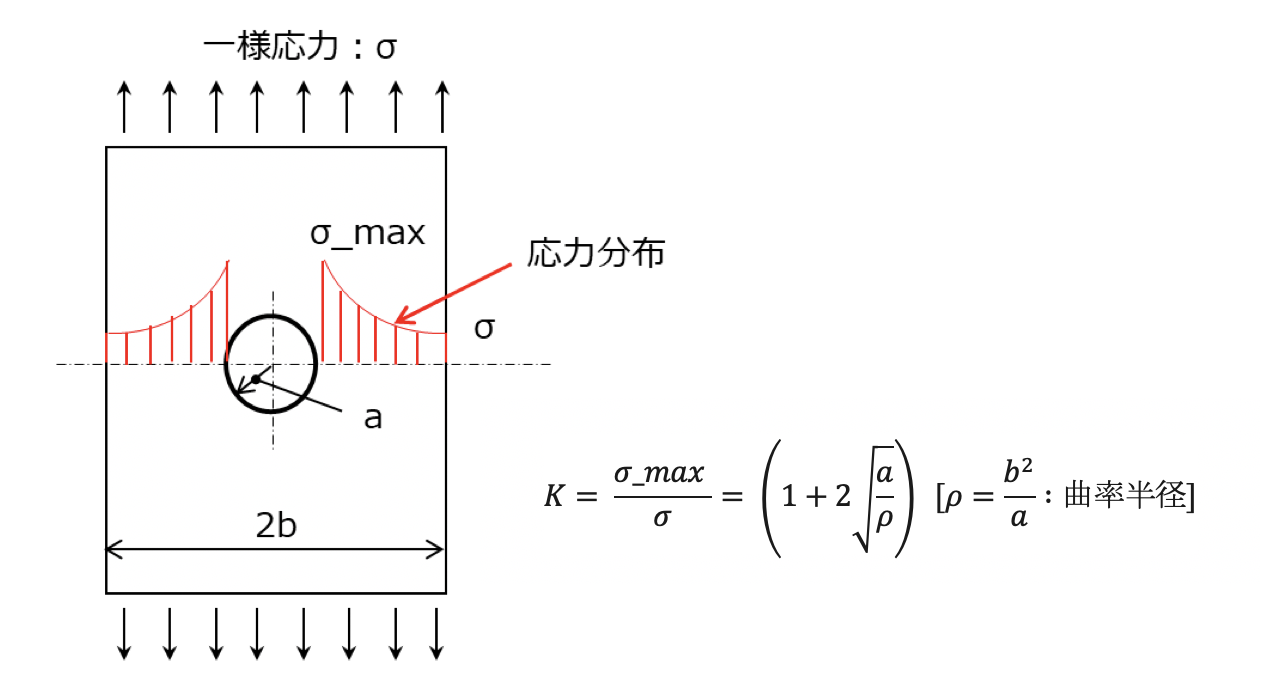
曲率半径を算出する。
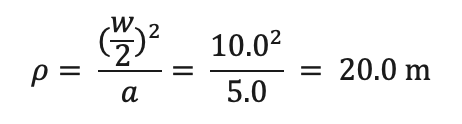
したがって、応力集中係数:Kの値は、
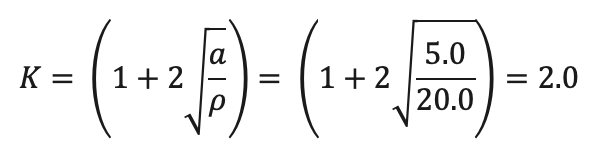
となる。
【負荷応力:S、応力比:R】
負荷応力:Smaxを算出する。
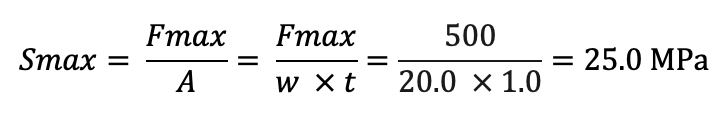
また、最小負荷応力は0となるため、応力比:Rは、
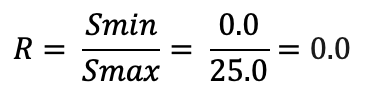
となる。
【材料許容応力:σall】
材料許容応力はS-N曲線から読み取るが、S-N曲線は一定の応力集中係数の条件下での試験結果を表しているため、計算で求めた応力集中係数から線形補完することで材料許容応力を算出する。

例えば、次に示す2つの試験データσ1とσ3が存在している場合で考えてみましょう。
応力集中係数:K1 = 1.0の時の材料許容応力:σ1および、応力集中係数:K3 = 3.0の時の許容応力:σ3がそれぞれ、σ1 = 200.0 MPa、σ3 = 150.0 MPaとなる時、応力集中係数:K = 2.0の時の材料許容応力:σallは、
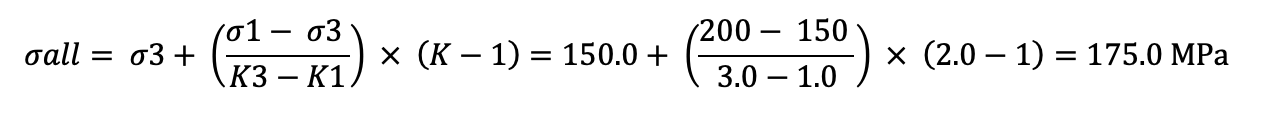
【疲労強度】
これまで算出した値から、材料許容応力と負荷応力および応力集中係数を比較すると、
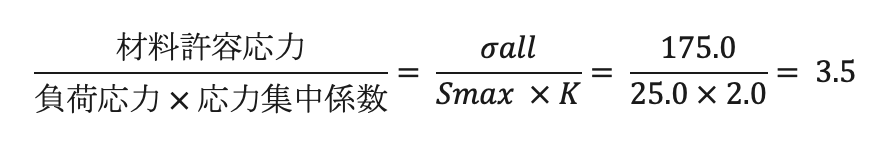
スキャッタファクタを考慮すると、材料許容応力と応力集中係数を考慮した負荷応力の比が2.0以上となるため、この部品の疲労強度は問題ありません。










