投稿日:2022年03月17日

学生時代に材料力学を学んだ方であれば「ヤング率(縦弾性係数)」という用語を聞いたことがあると思います。
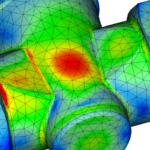
材料力学による「フックの法則」では、応力とひずみの間に比例関係があると定められ、ヤング率をEとして、垂直応力をσ、縦ひずみをεとすれば「σ=Eε」の関係式が成り立つため、材料の性質を調べる際に用いられます。
今回はこのヤング率に注目し、どのような場面で上記の関係式が活用されるか説明したいと思います。
基礎的な応力とひずみの知識
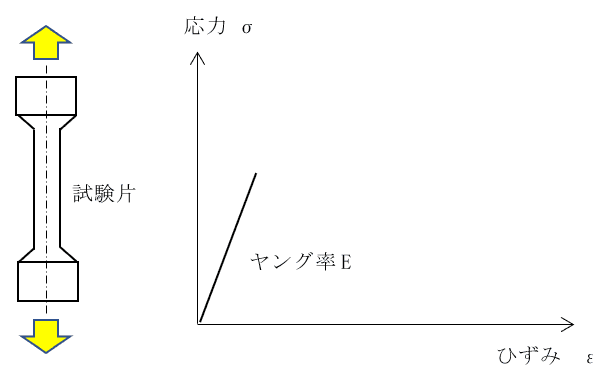
材料に荷重などの外力が加わると、その力に抵抗するために反対向きのベクトルで抵抗力が生じます。
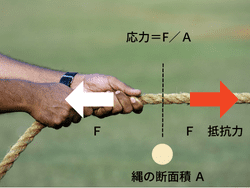
その単位面積についての抵抗力の大きさを表したのが「応力(σ)」です。
機械的性質(力学的特性の総称)を表す物理量となる応力は、材料力学で非常に重要な概念となり、引張応力、圧縮応力、せん断応力など様々な種類があります。
また、物体に応力が発生すると同時に変形も現れます。
この変形した物体と比較し、元の状態に対して変化した度合いを「ひずみ(ε)」と呼びます。
材料の初めの長さをℓとした場合、外力を加えた長さをℓ’とすると、関係式は「ε=(ℓ’―ℓ)/ℓ」が成り立ちます。
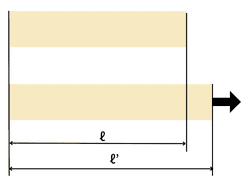
ひずみには縦ひずみ、横ひずみ、せん断ひずみ、体積ひずみなどがあり、応力と同様に材料力学において重要な概念の一つとなります。材料の機械的性質を調べるため、最も基本的な試験が「引っ張り試験」であり、測定値を比較できるようにJISで試験方法が決められています。

引っ張り試験から導き出された「応力―ひずみ線図」では、応力とひずみには正比例の関係があり、弾性限度(点a)を超えると物体に塑性変形が生じ、外力を取り去っても元の形に戻ることはありません。
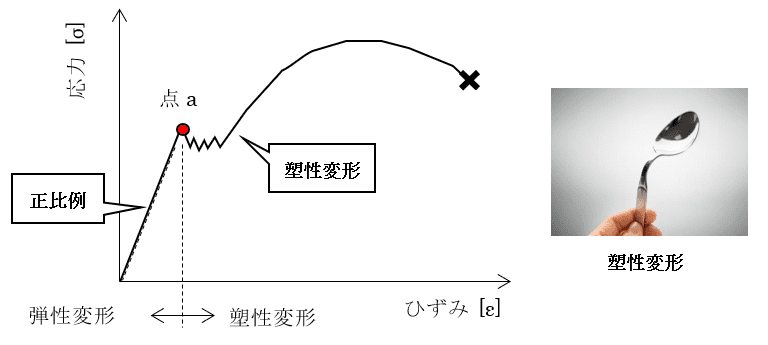
改めて知っておきたいヤング率と応力、ひずみの関係について
金属の材料にはそれぞれ特徴があり、その特徴を定義する一つに「ヤング率(E)」があります。
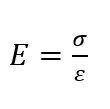
ヤング率は縦弾性係数とも呼ばれ、「弾性」とは材料に外力を加えた際、その外力を取り去ると元の形状に戻る性質のことです。
また、ヤング率が大きいほど剛性の高い材料ということになり、変形のし難い材料の目安となります。
※この「剛性」ですが、あくまで変形のし難さを表す度合いであり、壊れ難いという意味ではありません。
材料は外力を加えると、内部で「応力」と「ひずみ」が発生します。
応力は外力に抵抗する力なので、外力を取り去れば応力とひずみも自然と消えますが、材料の耐え得る応力を超えるとひずみによる変形が残ってしまいます。
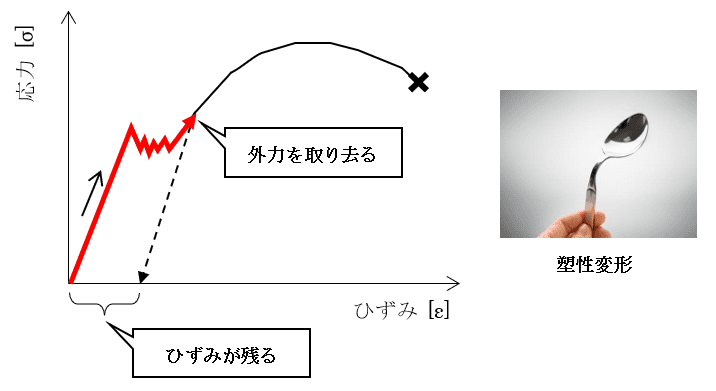
応力やひずみ量が分かれば材料の変形を防ぐことができるため、そこで活躍するのが「σ=Eε」の関係式です。
半径5mm、長さ1mの鋼材丸棒を30kNの力で引っ張った時の変形量を求めてみましょう(※問題1)。
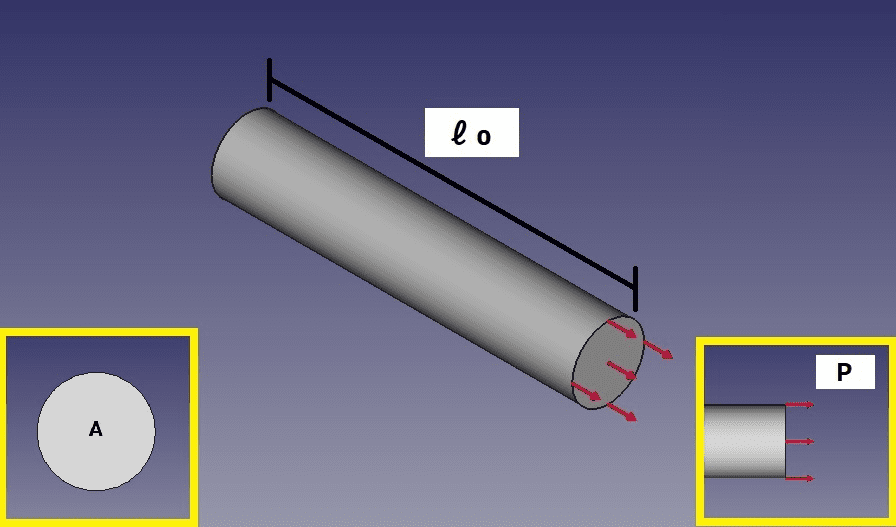
問題1:鋼材丸棒を引っ張った場合
ここでのPは外力、Aは丸棒の断面積(78.5mm^2)、ℓ₀(100mm)は丸棒の元の長さを指しています。
垂直応力σは「σ=N(断面に垂直な内力)/A」で算出が可能なので、引っ張りに対する内力はP=Nとなり、30×10^3/78.5=382MPaとなります。
ひずみεは「ε=σ/E」で求めることができるため、鋼材のヤング率は205GPaと定めた場合、382/205×10^3=1.86×10^-3となります。
棒の伸びλは「λ=εℓ₀」なので、棒が伸びる長さは1.86×10^-3×100=1.86(mm)と求めることができます。
ヤング率の他の例として、銅(129.8GPa)、鋳鉄(152.3GPa)、アルミニウム(70.3GPa)などがあります。
ヤング率とポアソン比の関係について
CAEを活用して応力などを調べる際、材料の機械的性質を入力する項目に「ヤング率」と「ポアソン比」しかないことが分かります。
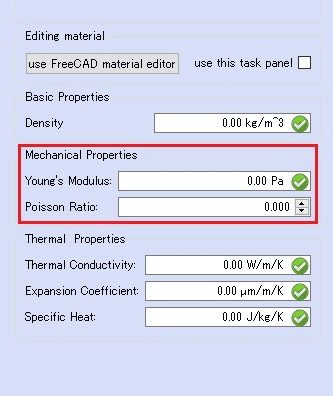
ヤング率は先ほど縦弾性係数と述べましたが、横の弾性係数を入力する必要はないのかと疑問を持つ方もいると思います。
物体に外力が加われば、あらゆる方向にひずみが発生するため、縦だけでなく横のひずみも考慮に入れなければなりません。
※実際は体積弾性係数(物質の圧縮に対する耐性)も考慮に入れる必要があり、ヤング率、せん断弾性係数、体積弾性係数の3つが物体に作用します。
横弾性係数は別名「せん断弾性係数(G)」とも呼ばれ、せん断応力(τ)とせん断ひずみ(γ)の関係式も「τ=Gγ」で成り立ちます。
しかしながら、CAEの入力項目はヤング率のみなので、一見するとせん断弾性係数は必要ないと思ってしまいます。
そこで登場するのがポアソン比(ν)です。
ポアソン比を簡単に説明すると、縦ひずみと横ひずみの比率であり、材料固有の定数となります。
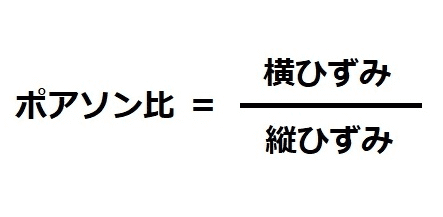
板の鋼材に一定方向に外力を加えた場合、「εx=σx/E」の関係が成り立ちますが、ここへ直角方向へのひずみ(εy)を考慮するため、ポアソン比を含めた関係式が以下になります。
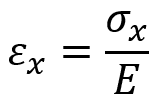
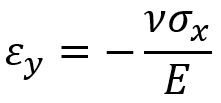
ポアソン比の例として、鋼(0.28~0.30)、鋳鉄(0.27)、アルミニウム(0.345)などがあります。
問題1の鋼材丸棒を30kNで引っ張った場合、直径の変化量を求めるには「Δd=d₀νε」の関係式を利用して、10×0.28×1.86×10^-3=5.2×10^-3(mm)が答えとなります。
この辺りは難しく考えず、ヤング率とポアソン比の2つがあれば、物体の応力やひずみ、変化量を求めることが可能であることを覚えておきましょう。
まとめ
いかがでしたでしょうか?
ヤング率やポアソン比は、材料の応力やひずみを調べる際に用いられるため、CAEを活用する方は調べる機会も多いかと思われます。
強度計算や固有値解析には欠かせない特性値なので、これらの業務に関わる技術者は必ず覚えておきましょう。