投稿日:2021年11月09日
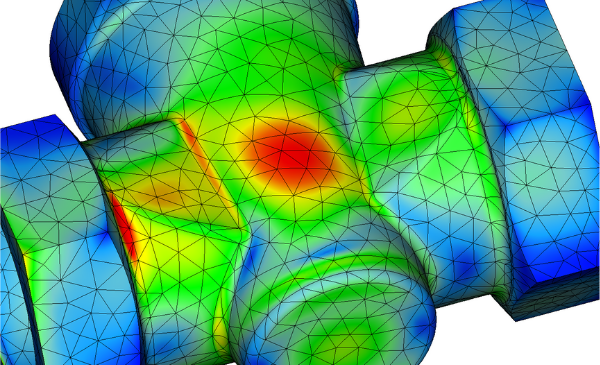
CAE(Computer Aided Engineering)を用いた強度評価では、「ミーゼス応力」の理解は必須ですが、大学で学ぶ材料力学の教科書にはミーゼス応力は載っておらず、耳慣れないものではないでしょうか?
このコラムでは、強度設計におけるミーゼス応力の意味と実務での使用例を紹介します。
CAE解析で「出力された応力の結果をきちんと評価できていない!」という方はぜひ参考にしてください。
このコラムを書いた人

強度、振動解析の専門家
計算力学技術者(固体)、(振動)の1級を保有。航空機メーカーで10年、自動車メーカーで3年、それぞれ強度と振動の解析業務を担当する。現在は車載機メーカーで製品の強度・振動の保証業務の取りまとめ役。過去の経験や専門知識を活かして、悩める設計初心者に情報を発信する。趣味はサイクリング、2児の父として家庭と仕事の両立に日々邁進中。
ミーゼス応力の定義
ミーゼス応力(またはフォン・ミーゼス応力)は、材料の降伏理論である「せん断ひずみエネルギー説」に基づいて算出される値で、材料の単軸降伏応力である σy 以上になると塑性変形します。
定義を読んでもピンと来ない方も多いのではないでしょうか。はじめての方には、ちょっと難しいお話かもしれませんので、基礎の部分から“かみ砕いて”説明を進めていきます。
通常、材料が引っ張られた時の強度を評価するには、図1に示すように単軸方向(一方向)に棒状の試験片を引っ張ってテストします。
そして、単軸方向に引張荷重を負荷すると図2のように応力とひずみの関係を表す線図を得ることができます。このとき材料が塑性変形をはじめるときの応力が降伏応力σyです。

さて、実際の設計部品には、様々な方向から力が加わったり、複雑な形状をしている部品も多いため、先ほど例で示した試験片のように一方向の単純な応力にはなりません。
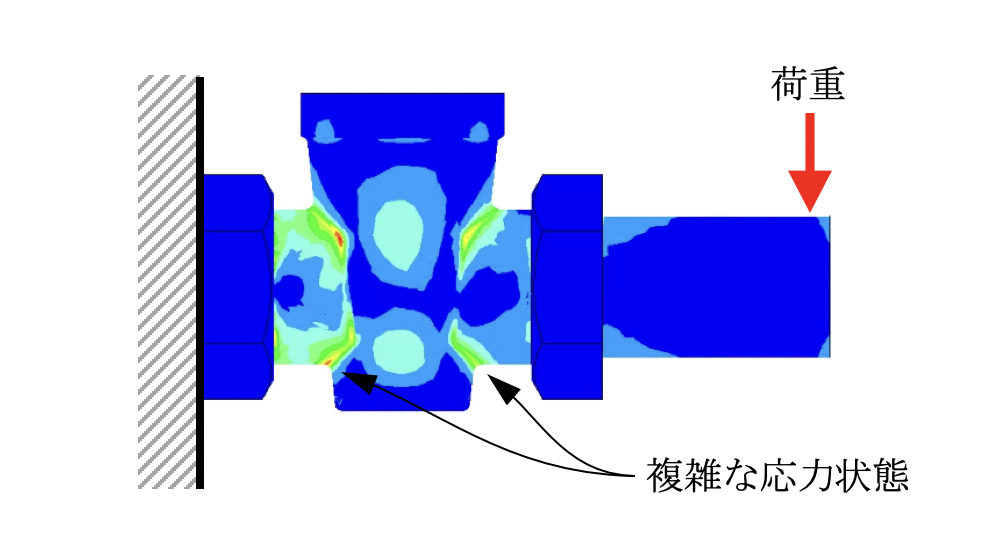
このようなケースでミーゼス応力を使うと、3次元の部品に働く複雑な応力状態を正のスカラー量(大きさのみを持つ量)として定義でき、一方向の応力で評価することができます。
このようにミーゼス応力は、複雑な応力の評価に便利なものであり、CAEが活用されるようになってから多くの強度評価で使用されるようになっております。
ただし、定義式が若干複雑なので、手計算や電卓を使ってミーゼス応力を算出することは実務ではほぼありません。
【ミーゼス応力の公式】
まず、公式を見てみましょう。専門書を開くと、ミーゼス応力(σvm )の公式として、次のような難しい式が記載されています。
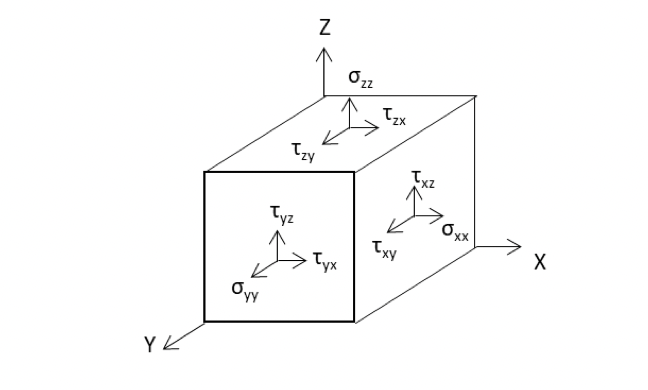
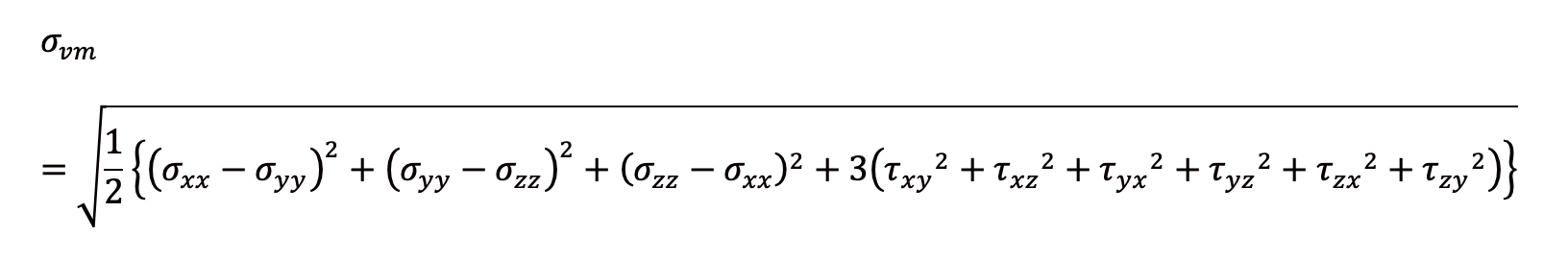
ここで、
σ1:最大主応力
σ2:中間主応力
σ3:最小主応力
とすると、以下のように式を単純化できます。
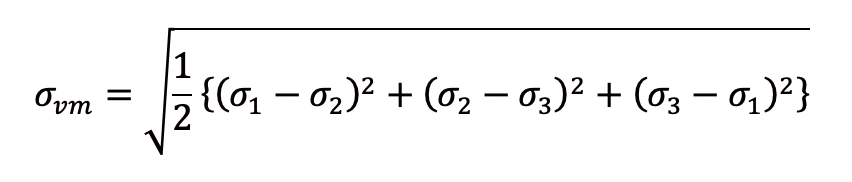
※詳しい主応力の説明は後ほど行います。
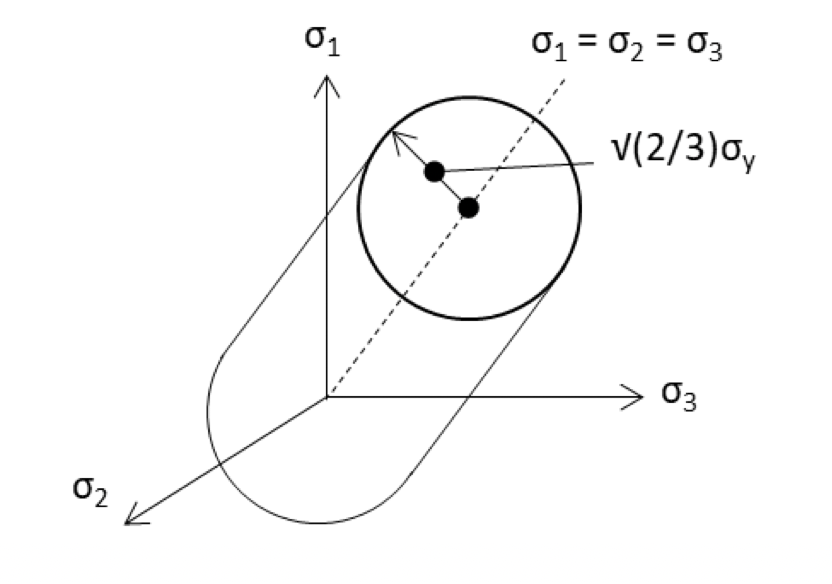
ミーゼス応力は、主応力を3つの軸とした「主応力空間」で考えると、半径が √(2/3)σy の円柱で図示できます。この円柱は、材料が弾性変形をする範囲を表しています。具体的には、次のようになります。
- 円柱の内側:材料が弾性変形している状態(材料が元に戻る変形)。
- 円柱の表面:材料が降伏状態(材料の変形が始まる限界)。
- 円柱の外側:材料が塑性変形している状態(元に戻らない変形)。
主応力との違い
【主応力の概要】
強度評価に用いられる応力の指標に「主応力」があります。
主応力とは、部材に引張、圧縮、せん断など複数の力が同時に働いている場合、その中で特に重要な「最大の引張力」や「最小の引張力(または最大の圧縮力)」を表すものです。簡単に言うと、材料が「一番引っ張られている方向(最大主応力)」や「一番押しつぶされている方向(最小主応力)」を示します。
次に、2次元と3次元で主応力の概念を説明します。ただし、初心者には理解しづらい概念であるため、ここではすべてを理解できなくても、上記の赤文字で示した基本的な説明がわかればとりあえず大丈夫です。
主応力の例(2次元の場合)
下図左は、部材にせん断応力(斜めに切る力やずれる変形)のみが働いている状態を示しています。この部材について、45°傾けた方向で切り取って応力状態を確認すると、下図右のようになります。このとき、せん断応力は0となり、代わりに引張応力と圧縮応力が働きます。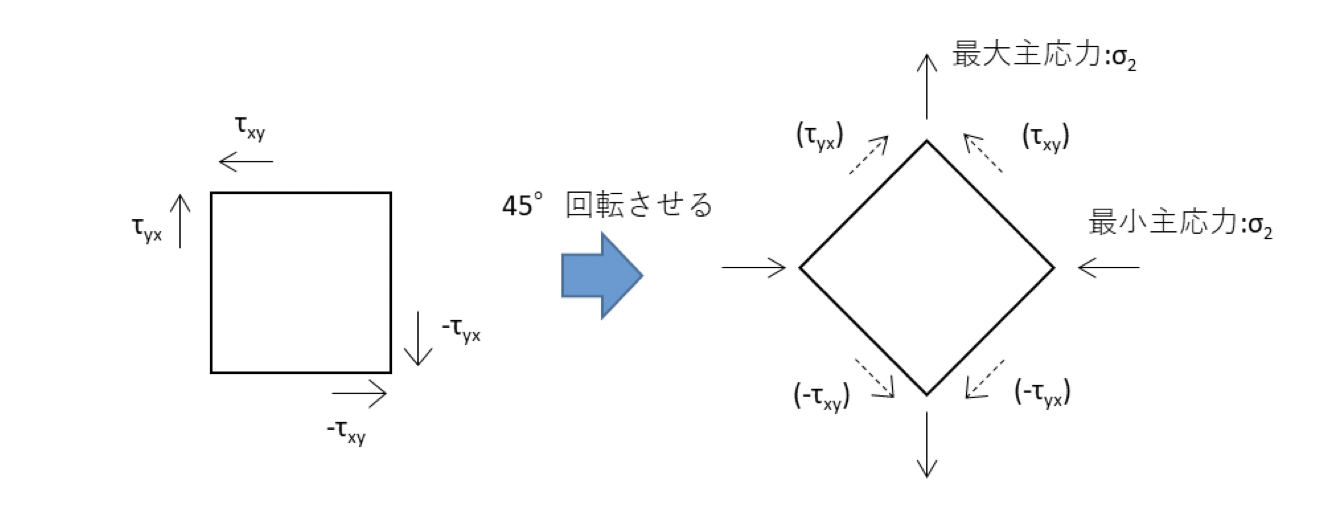
つまり、主応力とは「せん断応力が0になる方向」での最大・最小の応力を指します。
3軸状態の場合
部材に3つの異なる方向に応力が働く場合(3軸状態)には、中間主応力というもう1つの応力が加わります。(中間主応力の詳しい解説はここでは割愛します。)
より詳しく学びたい方へ
主応力について少しイメージが難しかったかもしれません。主応力は、材料内部の応力がどのように働くかを示したものです。詳しい解説を行うと、多くの図が必要になるため、ここでは簡単に説明しましたが、より詳しく理解したい方は、弊社Eラーニングで学べます:強度設計入門講座
【主応力とミーゼス応力の差】
具体的な数値を使って、主応力とミーゼス応力の違いを比較してみましょう。ここでは、計算をシンプルにするために2次元の状態を考えます。
2次元状態のミーゼス応力の式
2次元の場合、ミーゼス応力は次の式で表されます:
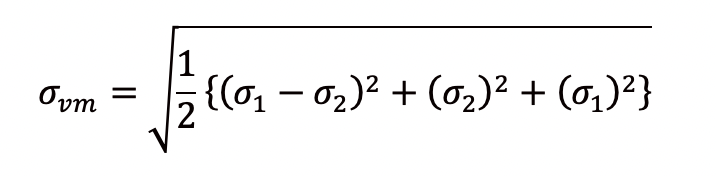
この式は、3次元状態の式から、中間応力の σ3 を取り除いたものです。
Case1:最小主応力が0、最大主応力が引張の場合
σ1 = 300 MPa、σ2 = 0 MPaとすると、
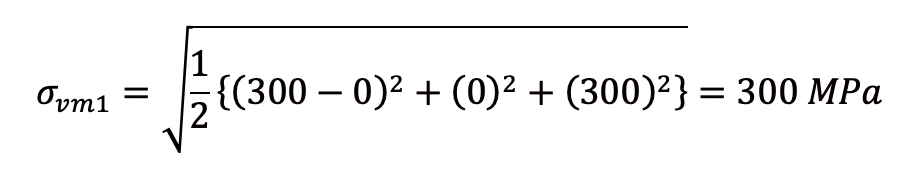
となり、ミーゼス応力は最大主応力と同じ値となります。
Case2:最小、最大主応力が引張の場合
σ1 = 300 MPa、σ2 = 50 MPaとすると、
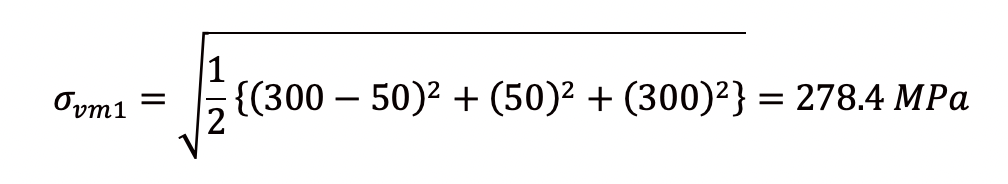
となり、ミーゼス応力は最大主応力よりも小さくなります。
Case3:最小主応力が圧縮、最大主応力が引張の場合
σ1 = 300 MPa、σ2 = -50 MPaとすると、
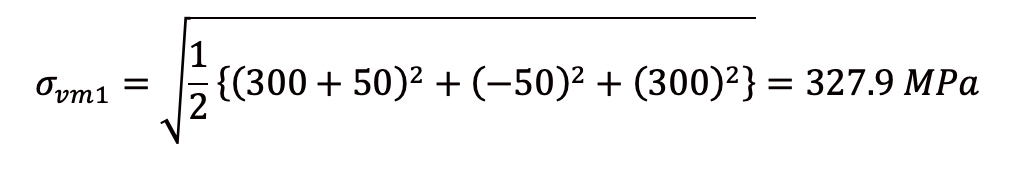
となり、ミーゼス応力は最大主応力よりも大きくなります。
まとめると、以下のようになります。
- 最小主応力がゼロの場合、ミーゼス応力は主応力と同じになる。(Case1)
- 最小主応力と最大主応力が同じ符号の場合、ミーゼス応力は最大主応力より小さなる。(Case2)
- 最小主応力と最大主応力が異なる符号の場合、ミーゼス応力は最大主応力より大きくなる。(Case3)
これらの計算を通じて、ミーゼス応力は材料内部の複雑な応力状態(ここでは2つの主応力)を1つの値にまとめることができることがわかりました。そして、この1つの値にまとめたミーゼス応力は、破壊の基準として利用できます。
それでは、次に具体的な使い方を見ていきましょう。
ミーゼス応力を用いた強度評価
強度評価の流れ
金属材料の降伏判定にミーゼス応力を用いることは常識となっています。
ミーゼス応力が使用できるのは「弾性・塑性変形域を持つ材料」です。例えば、鉄やアルミです。
鉄以外の「非金属材料」でも「引張りと圧縮で挙動が大きく異なるコンクリートのような材料」を除くとミーゼス応力が使われます。
ただし、ミーゼス応力の計算結果には「マイナスの値」が無いため、応力の引張・圧縮の区別ができません。例えば、CAE解析を行った結果、赤く示されている部分が見つかっても、色が赤く表示されるだけで、この応力が引張なのか圧縮なのかわからないということです。
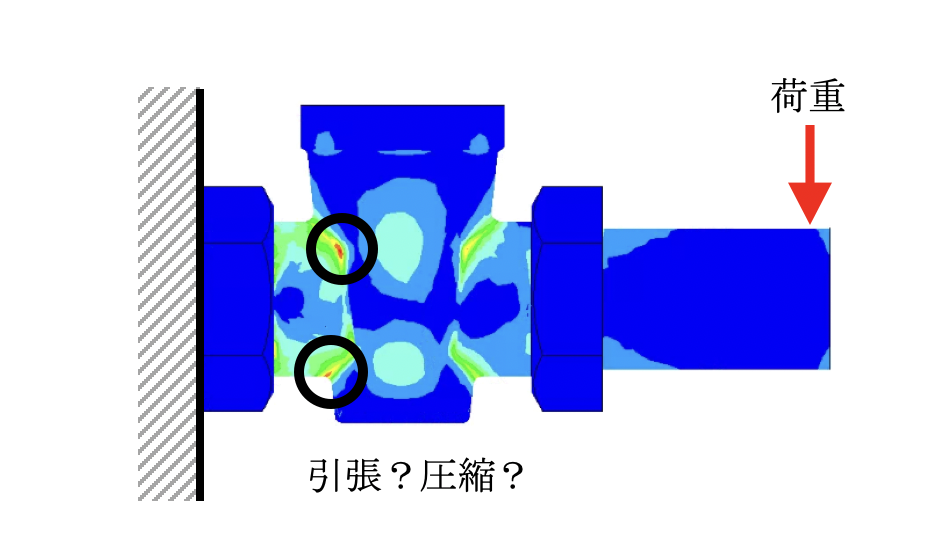
従って引張・圧縮の判定には主応力値を使用します。
なぜなら、主応力にはマイナスの値があるからです。
実際のCAEを用いた強度評価の流れは、
- CAEモデルから、部材に加わるミーゼス応力の最大値を算出する
- ミーゼス応力の最大値発生部の主応力の値から、応力状態(引張or圧縮)を判定
- 引張または圧縮の材料許容値σyをJIS Handbookなどから抽出する
- 安全率を考慮して、降伏判定を行う
という順番で強度評価を行います。
具体的な値を用いた強度評価
では実際の材料許容値を用いて、強度評価を行ってみましょう。
ある2次元要素でモデル化した部材の応力状態、材料許容値を示します。
- 材料:SS400
- 引張強度:400 MPa
- 引張降伏応力:245 MPa
- 安全率:4
- ミーゼス応力の最大値:90.4 MPa
- 最大主応力:85 MPa
- 最小主応力:-10 MPa
このモデルで、最大ミーゼス応力が発生する箇所では、最大主応力が最小主応力の絶対値よりも大きいため、引張応力が支配的であることが分かります。
従って降伏判定は引張降伏応力とミーゼス応力を比較します。
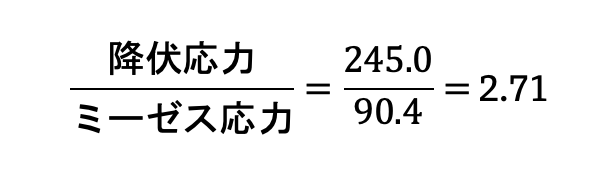
安全率を考慮すると、ミーゼス応力と降伏応力の比が4以下となり部材が降伏するため、設計変更が必要です。











