平行軸の定理を理解しようとして、「公式は知っているが、使い方がわからない」「断面二次モーメントと慣性モーメントの違いがイメージできない」と悩んでいませんか？

これらの知識は設計や解析の現場で求められる知識ですが、直感的に理解しづらいと感じる人も多いでしょう。曖昧なままでは計算ミスにつながり、設計の精度に影響を及ぼします。

本記事では、平行軸の定理の基本から実務での活用例までをわかりやすく解説します。最後まで読めば、設計や解析の精度が向上し、より合理的な構造設計ができるようになります。

平行軸の定理は2種類のモーメントに適用できる

平行軸の定理は、回転体や構造部材のモーメント計算に不可欠な基礎理論です。特に、断面二次モーメントや慣性モーメントを重心以外の回転軸に適用できる点が実務で役立ちます。

機械設計では、シャフトやフライホイールの強度評価、ロボットアームの運動解析などに不可欠です。

断面二次モーメントと慣性モーメントの関係や違いについては以下の記事をご覧ください。

断面二次モーメントの平行軸の定理

断面二次モーメントの平行軸の定理は、剛性計算に有用な理論です。特に、梁やギアシャフトなどの構造解析において、異なる軸に対する剛性や強度を求める際に活用されます。

重心軸から離れた位置に作用する荷重の影響を正確に評価できるため、CAE解析や動的シミュレーションでの計算精度向上にもつながります。機械設計における構造最適化や材料コスト削減を実現するための重要な知識です。

断面二次モーメントとは

断面二次モーメントは、構造物の断面の形状が変形にどの程度抵抗するかを示す指標です。これは、曲げモーメントの影響を受ける部材の剛性を評価するために用いられます。

たとえば、細長い梁と厚みのある梁では、同じ材料を使用していても剛性が異なります。この違いを数値化するのが断面二次モーメントです。

図に図心を基準とした任意断面を示します。

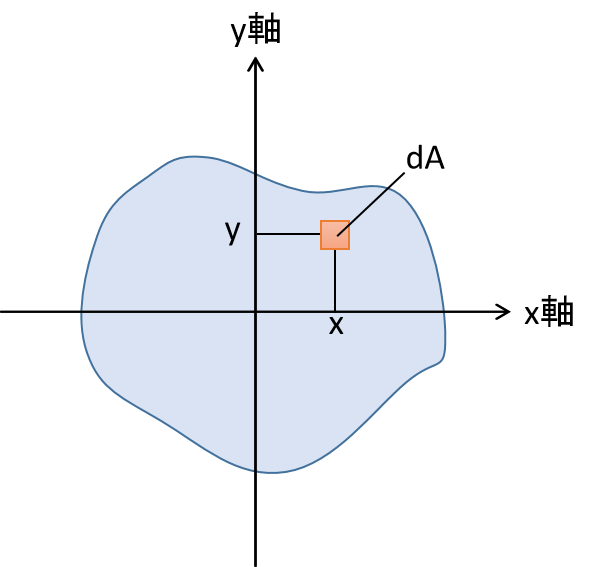
X軸、Y軸に関する断面二次モーメントは以下で表されます。

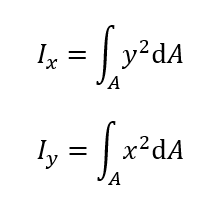
ここで、Ix はx軸回りの断面二次モーメント、Iy はy軸回りの断面二次モーメント、dA は微小面積要素を表します。物体の形状に応じて積分計算を行うことで、その軸に対する断面二次モーメントを求めることができます。

ここでは、具体的な事例を通じて、断面二次モーメントに対する平行軸の定理の実践的な使い方を解説します。

断面二次モーメントの平行軸の定理

断面二次モーメントの平行軸の定理は、図心を基準とした断面二次モーメントが分かっている場合、任意の軸に対する断面二次モーメントを導けます。

平行軸の定理の公式は以下で表されます。

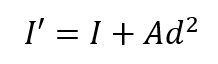
ここで、 I’ は新しい軸に関する断面二次モーメント、 Iは図心を基準とした断面二次モーメント、A は断面積、 dは図心から新しい軸までの距離です。この公式を使えば、既知の断面二次モーメントから、任意の軸を基準にした断面二次モーメントの計算が可能です。

断面二次モーメントの計算

機械設計では、構造部材の断面二次モーメントを求めることが不可欠です。例えば、橋の梁や機械フレームの設計では、荷重に対する断面の剛性を考慮した断面二次モーメントの計算が必要になります。

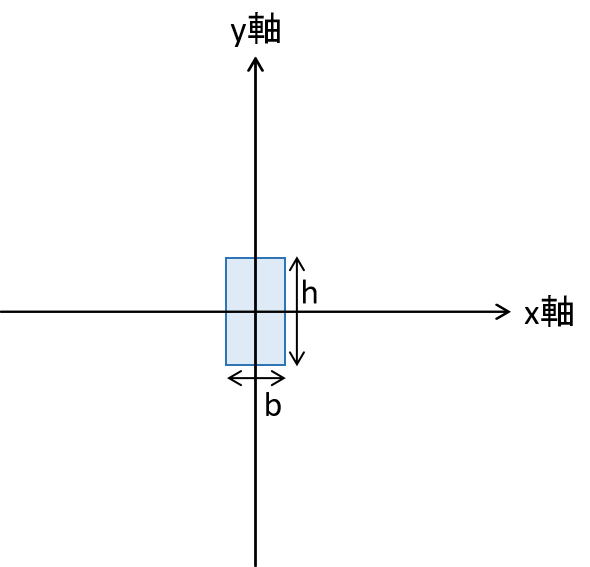
ここでは、矩形断面の例を考えます。図に図心を基準とした矩形断面を示します。x軸に関する矩形断面の断面二次モーメントの式は以下で表されます

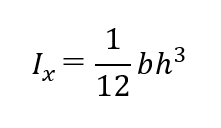
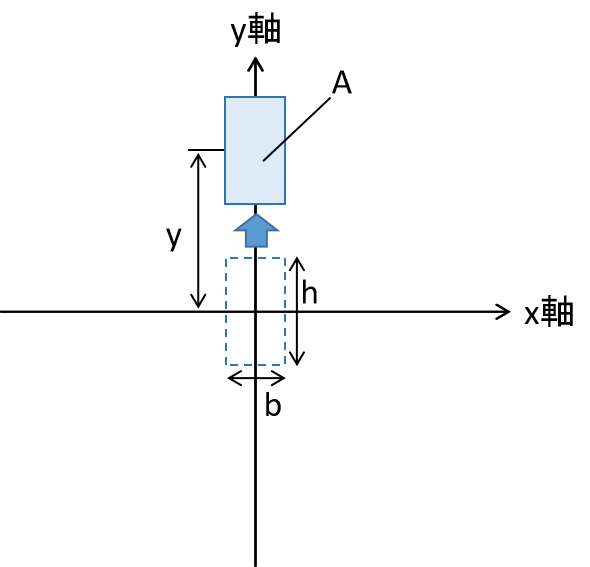
続いて、矩形断面が図心からy軸方向へ移動した場合を考えます。これは軸の位置が移動したことに相当します。図に図心からy軸方向へ移動した矩形断面を示します。

このとき、断面がy軸方向にyだけ移動した場合、x軸に関する断面二次モーメントに平行軸の定理を適用すると、以下の式が導かれます。

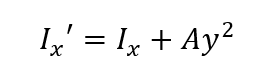
ここで、yは断面の移動距離です。また、Aは断面の面積です。従って、前述のIxおよび断面積bhを代入すると、以下の式になります。

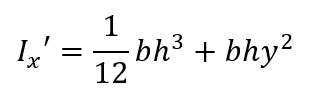
このように、平行軸の定理を利用すると、任意の軸を基準にした断面二次モーメントの計算が可能です。

慣性モーメントの平行軸の定理

慣性モーメントの平行軸の定理は、回転体の運動解析や機械設計において重要な役割を果たします。物体の回転軸が重心軸とは異なる位置にある場合、この定理を利用することで新しい軸に関する慣性モーメントを求めることができます。

慣性モーメントとは

慣性モーメントは、物体が回転運動をする際の回りにくさを表す指標です。質量が大きい物体や回転半径が大きい物体ほど、慣性モーメントの値も大きくなります。この特性は、機械設計やロボット工学など、さまざまな分野で利用されています。

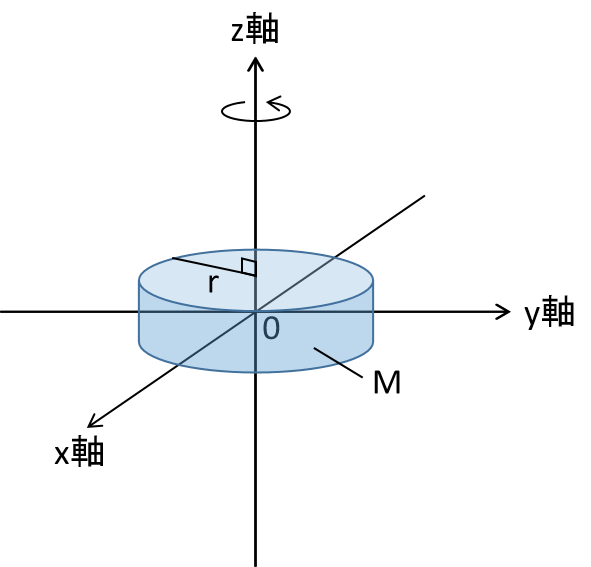
図に密度が均一で連続体である剛体を示します。

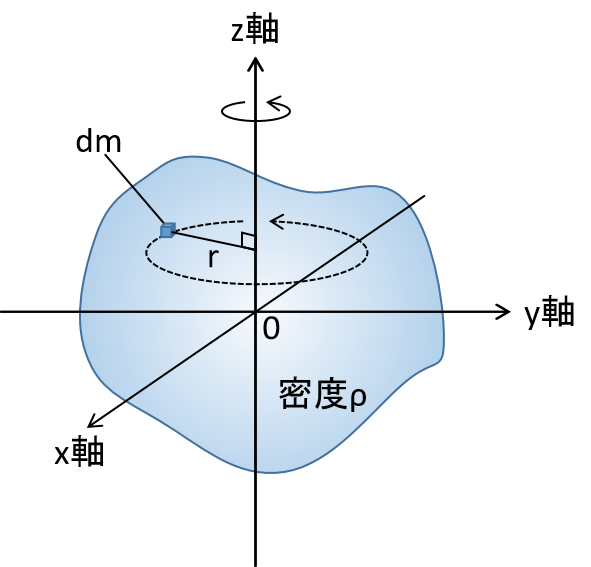
このとき、Z軸を回転軸とした慣性モーメントの式は以下で表されます。

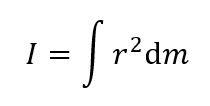
ここで、Iは慣性モーメント、dmは剛体の各微小部分の質量、rは回転軸から各微小部分までの距離を表します。

また、剛体の密度をρとすると、dmは微小体積 dVを用いてρdVと表現できます。したがって、I は以下の式で表されます

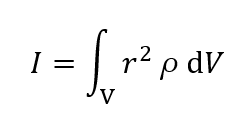
また、密度が均一なのでρを積分の外に出して、最終的に以下の式になります

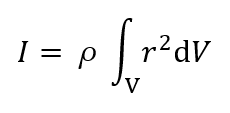
以上より、物体の形状に応じて積分計算を行うことで、その軸に対する慣性モーメントを求めることができます。

ここでは、具体的な事例を通じて、慣性モーメントに対する平行軸の定理の実践的な使い方を解説します。

慣性モーメントの平行軸の定理

回転体の慣性モーメントにおける平行軸の定理は、重心を基準とした慣性モーメントが分かっている場合、任意の軸に対する慣性モーメントを導けます。

平行軸の定理の公式は以下です。

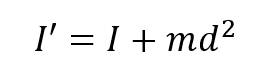
ここで、I’は新しい軸に関する慣性モーメント、Iは重心を基準とした慣性モーメント、mは回転体の質量、d重心から新しい軸までの距離です。この公式を使えば、既知の重心を基準とした慣性モーメントから、任意の軸を基準にした慣性モーメントの計算が可能です。

機械設計における慣性モーメントの計算

機械設計では、回転体の慣性モーメントを求めることが不可欠です。例えば、自動車のフライホイールやロボットアームの設計では、回転軸に対する慣性モーメントの計算が必要になります。

ここでは、円盤の例を考えます。重心を基準とした慣性モーメントは以下の式で求められます。

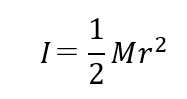
ここで、Iは慣性モーメント、Mは円盤の質量、rは円盤の半径を表します。

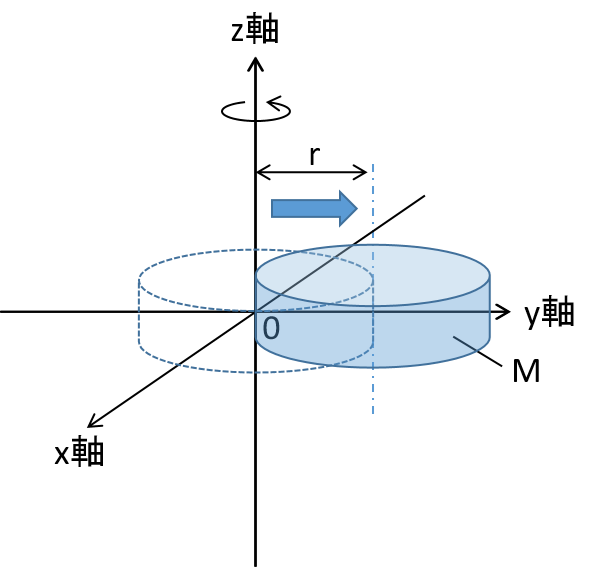
しかし、円盤が回転軸からずれた位置ある場合、新しい軸に関する慣性モーメントを求める必要があります。このとき、平行軸の定理を適用すると、以下の式が導かれます。

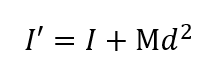
ここで、dは重心軸から新しい回転軸までの距離を表します。また、Mは円盤の質量です。

例えば、重心軸から新しい回転軸までの距離をrとすると、最終的に以下の式になります

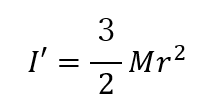
このように、平行軸の定理を利用すると任意の軸を基準にした慣性モーメントの計算が可能になります。

平行軸の定理まとめ

平行軸の定理は、断面二次モーメントと慣性モーメントの両方に適用できる重要な理論です。機械設計では、シャフトやフライホイールの慣性モーメント計算、梁の剛性評価などに役立ちます。

この記事では、定理の仕組みや計算方法、具体的な応用例を解説しました。この知識を活用することで、設計精度が向上します。計算時に迷った際は、ぜひこの記事を参考にしてください。

• メカトロ
• 強度設計