断面二次モーメントと慣性モーメント。どちらも大学で習ったことや業務で必要となり習ったことがある人も多いのではないでしょうか？

しかし、この2つを関連付けて考える人は少ないと思います。

本コラムでは断面二次モーメントと慣性モーメントの定義、及び二つの物理量の関係性をまとめました。

「どちらの値も聞いたことはあるけど良く分からない。」「設計者だけど初めて聞いた」といった方は是非本コラムで2つの概念について理解を深めてみましょう。

断面二次モーメント

断面二次モーメントとは？

断面二次モーメントは以前のコラムでも記載していますが、「断面形状による部材の曲げにくさ」を表す値です。

名前が示す通り「断面」の「形状」だけで決まる値で、単位は「mm^4：距離の4乗」です。断面二次モーメントが高い程曲げにくい形状となります。

断面二次モーメントは、建築物や構造物において、梁部材の様な曲げ力（モーメント）が働く時の計算に使用されます。

断面二次モーメントの定義式

以下のような断面において、x軸（図心を通る直線）を中心に回転する（曲げられる）場合の断面二次モーメント：Ixの定義式は、

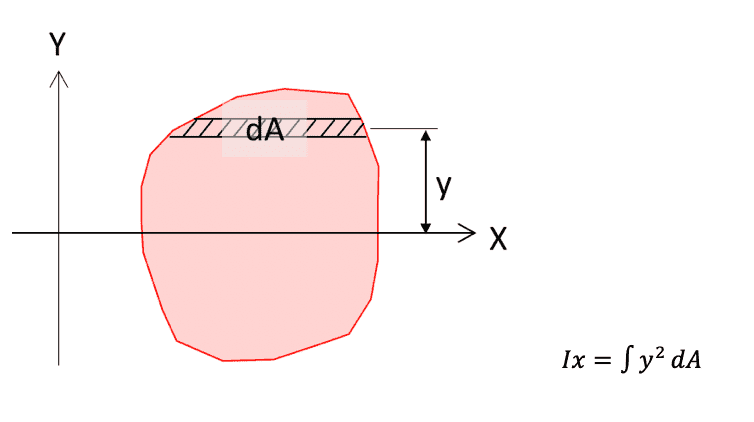
となります。

これは、「微小断面積：dA」に、dAからx軸までの「距離の二乗を掛けた値」を、「断面性全体で合計した値」を意味します。

断面二次モーメントは大学の工学部で習う「材料力学」の分野で出てくる難しい考え方であり、数式だけでその概念を完全に理解出来る人はほとんどいません。

初めて断面二次モーメントに触れたという方は、まずは上記の数式の意味をなんとなく理解しておきましょう。

慣性モーメント

慣性モーメントとは？

一方、慣性モーメントは「部材の回転しにくさ」を示した値です。

物体が回転運動をしているときに慣性モーメントが大きいと動き出すのに大きな力が必要となり、いったん動き出すと逆に止めるのにも大きな力が必要となります。

例として、下図のような2種類の車輪を回転させる場合を考えてみます。

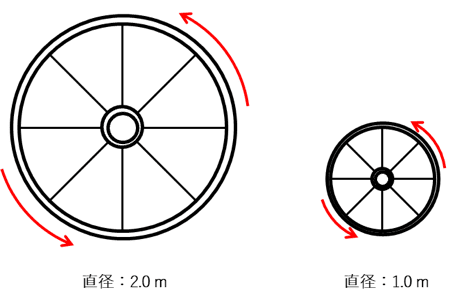
左図は直径2.0m、右図は直径1.0mとし、重さは同じとします。また回転軸は固定されているものとします。

この2種類の車輪を、止まった状態から回転させる時に必要な力はどちらが大きくなるでしょうか？

結論としては、直径2.0mの車輪の方が、回転させる時に必要な力は大きくなります。

この「回転のさせやすさ」、または「回転の止めやすさ」を定量的に表した値が慣性モーメントです。

慣性モーメントの定義

では慣性モーメントの定義式がどうなるかを、以下のような質点（重さのみを持つ要素）が、回転軸周りを回転する場合で考えてみましょう。

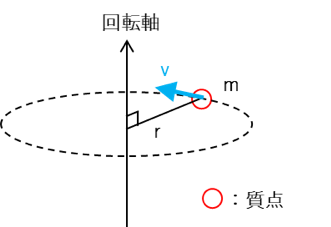
質量：m、回転軸からの距離：rとすると、慣性モーメントは、

I=m×r^2

となります。

次にこの式を用いて下図のような3次元方向に長さを持つ剛体の慣性モーメントを考えてみます。

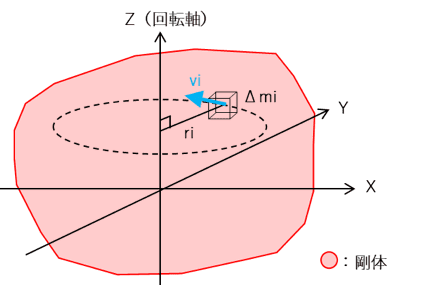
剛体を多数の微小体積要素に分解します。

分解した微小体積の質量をΔmiとし、微小体積から回転軸までの距離をriとすると、剛体の慣性モーメントは、

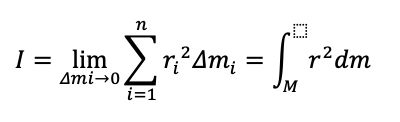
となります。

これは、微小要素の質量：Δmiを0に近づけていった結果、慣性モーメントが微小な体積から回転軸までの「距離の二乗：r2」を、「剛体の全質量：M」に渡って積分した値になることを意味します。

また、微小重量：dmは、剛体の密度：ρと微小体積：dVを用いると、dm = ρdVとなるため、剛体の慣性モーメントは、

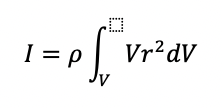
とも書くことができます。

並進運動と回転運動

慣性モーメントは、回転運動の力のつり合い式から求められる値です。

しかし、回転運動における速度である「角加速度」や、力である「トルク」などは普段馴染みが無い人には分かりづらい概念でもあります。

従って、直感的に分かりやすい並進運動と対比させることでイメージしやすくしてみましょう。

下表に固定軸まわりの回転運動と、x軸に沿った並進運動の対応関係を示します。

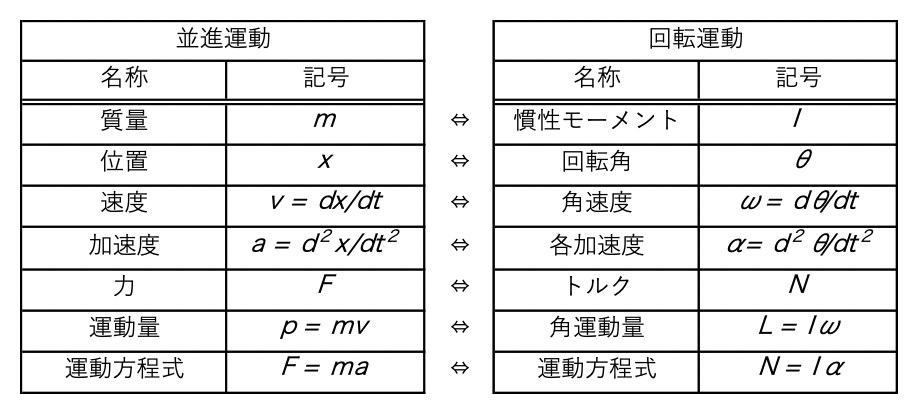
表から分かるように、慣性モーメントは並進運動における質量：mの役割を持つ物理量にあたります。

断面二次モーメントと慣性モーメントの違い

大学や業務で断面二次モーメントや慣性モーメントを学んだことがある方でも、お互いを関連付けて考える機会はなかなか無いのではないでしょうか？

しかし、実は断面二次モーメントは「慣性モーメント」とも呼ばれ、英語では「Moment of Inertia of Area：面積の慣性モーメント」と表現されます。

一方、動力学で使う「慣性モーメント：Moment of Inertia」は、別名「質量の慣性モーメント：Mass Moment of Inertia」と呼ばれ、断面二次モーメントと区別されています。

これは、断面二次モーメントと慣性モーメントはどちらもモーメント・トルクといった回転に対する抵抗力を示す値であるからです。

断面二次モーメントと慣性モーメントの関係を下表に示します。

静力学では物体が静止した状態の荷重のつり合いを考えるため、動力学と違って質量の影響がなくなります。

そのため厚さ方向の影響が無くなり、断面形状のみが影響される定義式となります。

動力学における慣性モーメントで、厚さ及び密度を単位長さ、単位密度とすると断面二次モーメントの定義式と同じになります。

従って、断面二次モーメントと慣性モーメントは、扱う分野は違いますが、本質的に同じ性質を示す物理量であると考えられます。

• 材料力学を学ぶ
• 機械力学を学ぶ