投稿日:2022年04月26日

設計をしていると、梁や柱の強度計算を簡単にサッと計算しておきたいといった場面がたまにあります。
たとえば、機器をデッキの上に設置したり、建屋の上層階に重量機器を設置する際に、念のため載せる梁の強度を確認しておこうかな、と思うのです。
そんな時に皆さんだったらどのように強度確認を行うでしょうか?
鋼材の強度を計算する学問に「構造力学」や「材料力学」などがあり、もし機械や建築の学科で学んでいるのであれば、一度は学習したことがあるのではないでしょうか?
図のように新人に「この青色梁の強度を手計算で確認しておいてー!」とお願いした際に、まじめな人ほど、不静定の梁で強度計算をしてしまうのです。

その時は「手計算なんだから、静定梁の条件で計算していいよ」と計算条件を変更するように促しますが、この条件が何を意味するかを知っているかどうかによって、強度計算のとらえ方は違ってきます。
その意図についてぜひ知っておいてください。
このコラムを書いた人

機械系プラントエンジニア
国内化学プラントで機械設計や建設工事を10年以上経験。危険物製造設備、発電・ボイラ設備・排水処理設備、研究施設の多種多様な設計・調達・工事に携わり、その知識をコラムにて発信中。現場でも活かせる専門知識を、日本のモノづくりに活かしてもらいたい!という強い思いを持っている。
不静定問題とは何か
不静定問題とは、構造力学において力のつり合いで問題が解けない問題を指します。たとえば、両端を固定している梁の両側には、梁が曲がろうとするモーメントが負荷することになります。
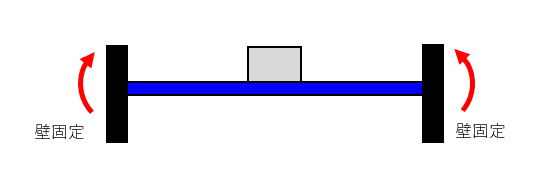
模式図.不静定梁
すると、途端に水平力と垂直荷重の力のつり合いでは、計算出来なくなってしまうのです。
その為、不静定問題を解く際は、「水平力のつり合い式」「モーメントのつり合い式」「梁たわみ量とたわみ角の関係」の3つの式から連立方程式で求めることになる為、非常に時間を要します。
一方で、静定問題は、下図のようにヒンジやピンで接合された状態で、梁の両端にはモーメントは発生しないという条件で計算できるため、力のつり合いで簡単に部材への荷重を計算することが出来るのです。
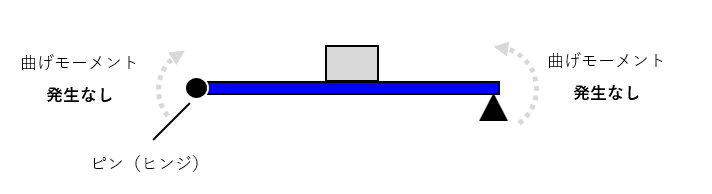
模式図.静定梁
上の図の静定梁と不静定梁の計算がどれほど計算するのが面倒かを計算してみると分かるかと思います。その違いを以下の模式図と計算式で示してみます。
下の静定梁と不静定梁の2つの計算では、梁に対して垂直に荷重Sという力が負荷している状態の両端に作用する反力を求めてみます。
反力を計算するときは、まずは荷重の釣り合いの式を立てます。この釣り合いの式は静定問題でも不静定問題でも特に変わりません。
しかし、モーメントの釣り合いの式を立てたときに、不静定問題では梁両端のモーメントが不明であるため、反力は求められません。その為、不静定問題では、別の理論式が必要になるのです。
静定梁と不静定梁との計算法の違いが分かりましたでしょうか?
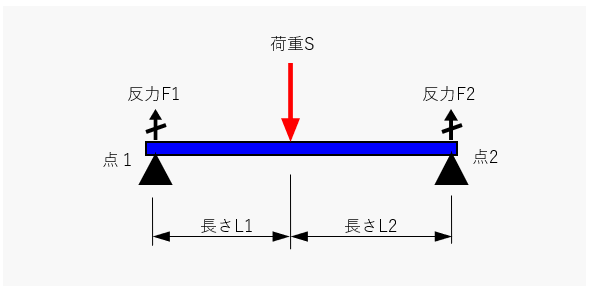
不明な値(荷重)がF1とF2の2つ存在する。荷重Sを受けているそれぞれの反力F1と反力F2を求めるには以下の計算を行う。
荷重の関係より F1+F2=S ・・・式➀が成り立つ。
又、点2まわりのモーメントの関係より
F1×(L1+L2) – S×L2=0 ・・・式➁が成立する。
式➁より、F1=S×L2/(L1+L2)
F1を式➀に代入して、F2=S×L1/(L1+L2)
よって変数の値=関係式であるため、2つの数式ですぐに両端の荷重を計算することができる。
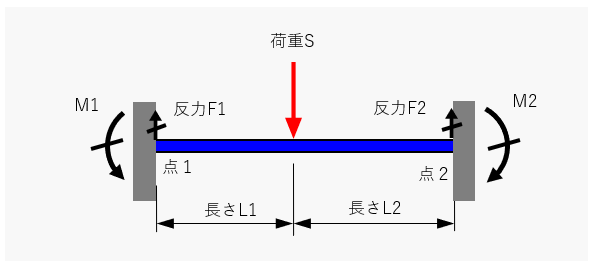
不明な値が壁からの反力F1とF2,両端のモーメントM1とM2 の計4つがある。荷重Sを受けているそれぞれの反力F1と反力F2を求める為に静定問題と同じ方法で立式してみる。
荷重の関係より F1+F2=S ・・・式➀ が成り立つ。
点2まわりのモーメントの関係より
F1×(L1+L2) - S×L2 - M1+M2=0 ・・・式➁ が成立する。
この2つの式では変数が多すぎて解けない!
※すべてがピン接合であれば静定問題となるので、ここでは静定問題=すべてピン接合として記載しています。逆に、静定問題ならすべてがピン接合であるというわけではありません。
機械設計者への補足として、手計算で梁の強度を計算する際に、不静定問題を扱わない方がメリットがある点についてもう少し触れておきます。
不静定梁で計算すると、その梁両端の接合点につながった別の部材からモーメントを受けることになります。このことは、その接合点を通してモーメントが伝わり、計算量はますます増えていくということになるのです。
何よりも考え方が複雑になっていくので、慣れないと頭を抱えることになります。よって手計算で簡単に強度計算をしたい場合は、接合点にかかるモーメントが一切かからない静定問題に置き換えて計算することをおススメします。
しかし、接合点の強度を確認する場合は、不静定問題を扱うことになるため、臨機応変に対応しなければなりませんね。
梁計算はトラス構造でとらえると簡単

梁の計算はまず、対象の全体構造をトラス構造に置き換えることで計算が簡単になります。
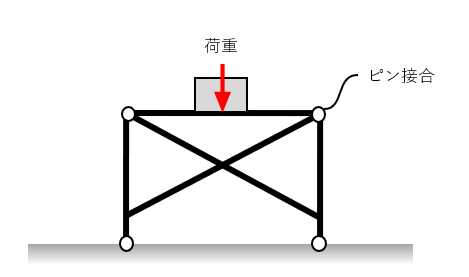
トラス構造とは、複数の3角形で構成される骨組構造で、その接合箇所は一般的にピン接合となっている構造です。(実際には溶接接合になっている場合もある)
タワーや橋なのでこの構造がよくみられます。トラス構造にすることで、部材の接合点にはモーメントが発生しない構造になり、すべての梁が静定梁と認識し、強度計算を行うことができるのです。
トラス構造が、手計算でも簡単に計算することができる理由は、トラス構造のどの範囲を切り取っても力のつり合いが保たれるという点です。その為、その部材に負荷する荷重が簡単に算出できるのです(下の模式図を参照)。
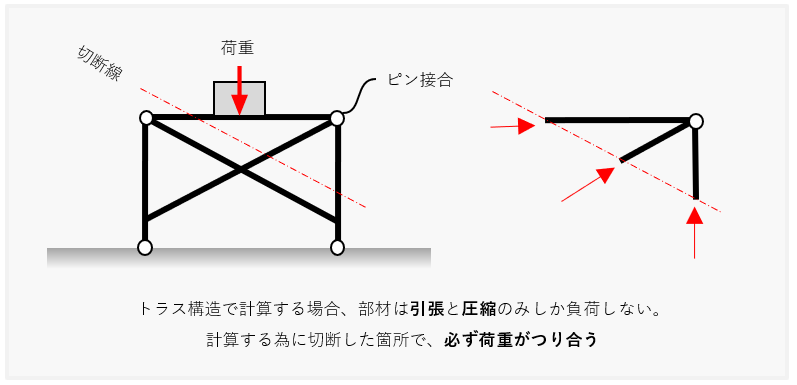
模式図.トラス構造の計算方法について
余談ですが、トラス構造を使ってトラス状に部材を組み合わせて作る「トラス梁」という部材があります。このトラス梁は、かつては今より計算ソフトがなく、H鋼等の部材が充実していない時期では、主に梁や柱に使用されることが多かったのですが、接合点が多くあるためその製造コストが高く、現在はその多くがH鋼や溝型鋼等の一般鋼材に置き換わっています。今でも体育館や倉庫の屋根の鋼材として残っているかと思います。
不静定梁での計算はどのような場面で使用されるか?
手計算では連立方程式を使用しないと強度計算が行えない不静定梁の計算は、どういった場合に計算しなければいけないでしょうか?
一般的なのはビルや住宅などの建造物に用いられます。

トラス構造で評価できるのはあくまで梁や柱のみです。それらが接合されている個所に関しては評価していないのです。
ビルや住宅といった建造物は、地震に対する耐震が求められます。耐震性をよくするには、各部材の接合点でどれくらいのモーメントを負担できるかを考慮しなければならないのです。
耐震性を担保するために、部材の接合箇所に加わる応力を算出しなければいけないのですが、ピン接合とする静定構造では接合点に付加する応力を正しく算出できません。
つまり、静定構造で計算するには、梁両端をピン構造で計算する必要があり、接合箇所の強度はモーメントを0としている為に評価出来ないのです。(実際の荷重よりも小さい値で評価してしまうため危険)
その為、梁の接合点の強度計算を行うには不静定構造で計算しなければいけません。
不静定梁で実際に計算するには、たわみ角方等の手法がありますが、構造が少しでも複雑になると、すべての梁柱の荷重とモーメントの式を連立方程式で計算することになるため、計算が非常に大変です。
当然手計算では、計算間違いも起きやすいため、一般に構造計算のソフトで計算します。
以上のことから、建築の分野では建造物の鉄筋や鉄骨といった部材の接合点では、どのような構造とすべきかをきちんと考慮した形状になっています。
たとえば、その接合点(ブラケットと呼ぶ)の扱いは特に注意を払っており、工事でブラケットを溶接し、それを現場で梁と高力ボルトで接合しています。さらに接合点の周りをダイヤフラムと呼ばれる補強板で部材の変形を抑えているのです。
模式図.梁柱の接合点(ブラケット)の構造
引用元:国立研究開発法人建築研究所
まとめ
簡単に梁や柱の強度を確認したい程度であれば、ピン接合と認識して静定梁で手計算した方が簡単に計算出来ます。しかし、ピン接合ではその接合点の強度が評価出来ていないということを踏まえていなければいけません。
これを理解せずにあなたが建築士に対して「ピン接合で材料強度を確認したから強度は大丈夫」と説明しても、安心してもらえないかもしれませんね。
参考:国立研究開発法人建築研究所WEBサイト「鉄骨造建築物の接合部ディテール例示資料集 ― 複雑な接合部ディテールの設計・製作の要点 ―」
URL:https://www.kenken.go.jp/japanese/contents/publications/data/143/index.html