ログイン投稿日：2022年05月05日
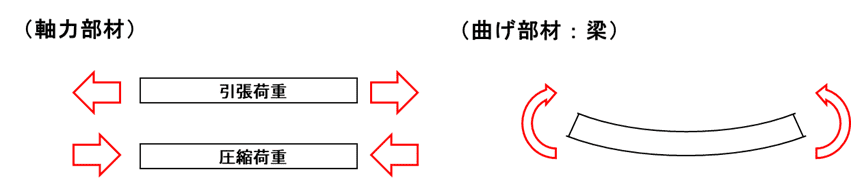
航空機において引張・圧縮荷重を受ける軸力部材は多くありますが、圧縮荷重による破壊モードは、引張荷重による破壊モードに比べて不安定現象（座屈）を考慮する必要があるため、引張荷重を受ける場合よりも注意が必要です。
このコラムでは航空機における、軸力部材に圧縮荷重が負荷される時の強度評価方法を解説しますが、軸力部材は航空機に限らず、トラスの部材や構造を結合する棒材などといったさまざまな機構に用いられる基礎的な機械要素です。
普段の業務において、航空機以外の製品における強度評価を行っている方も、是非本コラムを参考に、軸力部材に圧縮荷重が加わった時の破壊モード及び強度評価方法を把握し、業務に役立てて下さい。
（なお、本コラムに用いる数式は、「航空機構造解析の基礎と実際：滝敏美著」を参照しています。）
航空機における軸力部材
軸力部材とは？
軸力部材とは、主に軸方向の荷重を受け持つ部材のことです。
一方で、軸に対して垂直方向の荷重が働き曲げモーメントが発生する部材を曲げ部材（梁）と呼び、一般的に多くの構造物は「軸力部材」及び「曲げ部材」によって構成されます。（航空機や車は、軸力・曲げ部材に加えて「外板」を含む「セミモノコック構造」で構成されます。）
以下に、軸力部材だけを用いた代表的な構造である「トラス構造」を用いた橋を示します。
トラス構造は、軸力部材を3角形に結合することで、部材に曲げモーメントが発生しないようにした構造のことです。
トラス構造は橋以外に、「鉄塔」「自転車・バイクのフレーム」などの構造物に使用されています。
航空機の構造
航空機の構造は主に、客室や貨物などを載せるスペースとなる「胴体」と、主翼や尾翼などの揚力を発生させるための「翼」に分けられます。
胴体は乗客や貨物を載せる部分のことで、現代の多くの旅客機や輸送機は、広い空間を実現できる「セミモノコック構造」を採用しています。
セミモノコック構造は、胴体外形を維持するための「フレーム」、軸方向の荷重を受け持つ「縦通材」、曲げ・ねじり・せん断荷重を受け持つ「外板」から構成されます。
民間機の胴体は床で上下に分割されており、客室や操縦席を床上に、貨物室を床下に配置します。
翼には機体を浮かせる揚力を発生させる「主翼」と、水平飛行を安定させるための「尾翼」があり、断面形状を維持するための「リブ」、長手方向に延びる「縦通材」、そして「外板」で構成されます。
翼も胴体と同じようにセミモノコック構造をとることが多いですが、グライダや軽飛行機などの小型機の一部では「トラス構造」が用いられています。
航空機の構造に用いられる軸力部材
民間機の胴体や翼はセミモノコック構造をとることがほとんどです。
セミモノコック構造のミクロな領域における荷重状態に着目すると、胴体が受ける自重による曲げモーメントは上部が引張荷重、下部が圧縮荷重、側部がせん断荷重にそれぞれ分解されます。
したがって胴体の軸方向に配置される縦通材は、軸力部材として計算します。
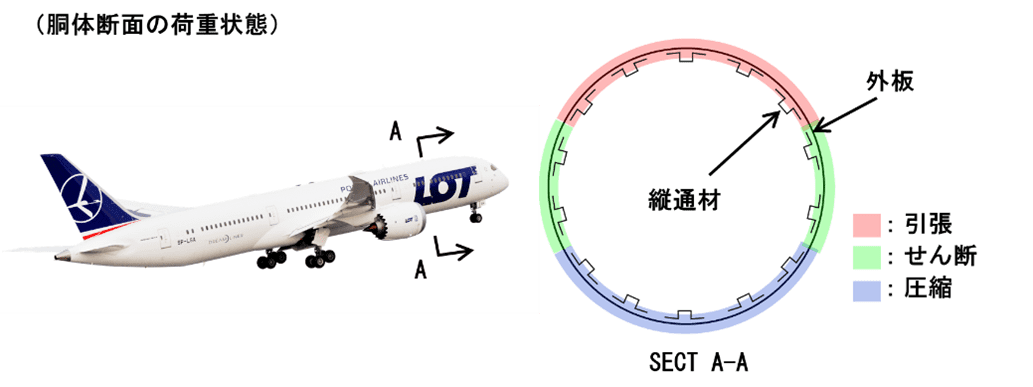
これは主翼や尾翼も同様で、胴体とは荷重状態が上下逆転し、上部が圧縮荷重、下部が引張荷重を受けます。
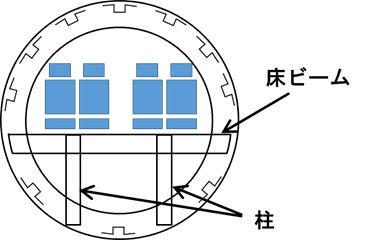
また、座席や乗客の重量を支えるための床の骨組みの中で縦方向の荷重を受ける「柱」も軸力部材とみなされます。
軸力部材の圧縮破壊モード
軸力部材の圧縮破壊モード一覧
軸方向に引張荷重を受ける部材の破壊モードが非常に単純であることに対して、軸方向に圧縮力を受ける部材の破壊モードにはさまざまな種類があります。
以下に、軸方向に圧縮荷重を受ける部材の破壊モード一覧を示します。
軸力部材の圧縮破壊モードは、主に上表の上から3つ（赤で囲った部分）であり、下の2つは各破壊モードが組み合わさった破壊です。
下図に示すように、各破壊モードは軸力部材の長さと、断面積に対する断面二次モーメントの比である、細長比によって変化します。
「航空機構造解析の基礎と実際：滝敏美著」から抜粋
なお、上表による分類はあくまで参考であり、実際の強度評価では同時に複数の破壊モードの許容応力・荷重を算出・比較しています。
材料圧縮破壊
板厚が厚く非常に短い、形状が安定した部材に圧縮荷重が負荷される場合に、圧縮降伏応力を許容値とする材料圧縮破壊が発生します。
材料圧縮破壊の許容値は、永久ひずみが発生する圧縮降伏応力：Fcyとしていますが、応力がFcyに達したあとも歪は増大するため、引張荷重が負荷された場合の引張終極応力（破断）のような許容値は定義出来ません。
材料圧縮破壊は純粋な材料特有の許容応力であるため、他の破壊モードの許容応力が圧縮降伏応力以上になることはあり得ません。
強度評価初心者の方で、Fcy以上の計算値をそのまま載せている方がたまにいますが、間違いですので注意するようにしましょう。
長柱座屈（オイラー座屈）
長柱座屈（オイラー座屈）とは？
下図のように、トラス部材のような棒状の長い真っすぐな部材に圧縮荷重が働いたときに、棒全体が横方向に曲がる現象を長柱座屈、またはオイラー座屈といいます。
上図は、片端固定・片端支持状態における長柱座屈を示しています。
長い棒状の部材に負荷する圧縮荷重を増加していくと、ある荷重に達すると急激に横方向の変形が増加し、曲げモーメントが発生することにより曲げ破壊が発生します。
長柱座屈(オイラー座屈)の算出方法
長柱座屈の許容値となるオイラー座屈荷重：PE,crは、圧縮ヤング率：Ec、断面二次モーメント：I、長柱の長さ：L、端末拘束係数：Cから以下で算出されます。
また、応力で表すと以下となります。
ここで、L’=L/√C：柱の座屈長さ、ρ=√(I/A)：断面の回転半径を示します。
端末拘束係数は端部の支持条件によって異なるため、下表の値を使用します。
「航空機構造解析の基礎と実際：滝敏美著」から抜粋
航空機の縦通材にように、外板によって座屈する方向が限定される場合を除いて、オイラー座屈荷重を計算する際に用いる断面二次モーメントは、最も小さくなる方向で計算する必要があるため、注意が必要です。
ねじれ座屈
ねじれ座屈とは？
薄肉断面の柱に圧縮荷重が負荷されたときに、曲げ剛性よりもねじれ剛性が弱い場合に発生する座屈現象をねじれ座屈と言います。
ねじれ座屈は、座屈による変形が主軸方向となる長柱座屈に対して、断面が回転しながらねじれるように変形する現象です。
ねじれ座屈は断面形状の対称性によって、許容値の計算式が異なります。
ねじれ座屈の算出方法
ねじれ座屈荷重の値は、2軸に対して対称となる断面と、1軸に対して対称となる断面でそれぞれ計算式が異なります。
各断面形状において、図心に圧縮荷重が負荷された場合の、両端単純支持梁（C=1.0）の軸力部材のねじれ座屈荷重は以下で算出されます。
[2軸に対して対称、非対称:ねじれのみ]
[1軸に対して対称:曲げとねじれの連成]
ここで、
A：断面積
Is：せん断中心周りの極慣性能率
Iy,Iz：断面二次モーメント
ys,zs：図心からせん断中心の距離
G：せん断弾性係数
J：サンブナンのねじり係数
Γ：ワーピング係数
Ｌ：軸力部材の長さ
をそれぞれ示しています。
また、ねじれ変形が発生する時の変形の中心をせん断中心といいます。
以下のようなC型断面の両端支持梁の中心に荷重を負荷する場合、せん断中心と荷重負荷点にオフセット距離があるとねじりモーメントが発生します。しかし、背部に位置するせん断中心上に荷重を負荷させると、ねじりモーメントは発生しません。
代表的な断面における、ねじり係数：J、ワーピング定数：Γ、せん断中心：eの算出式を下表に示します。
「航空機構造解析の基礎と実際：滝敏美著」から抜粋
クリップリング応力
クリップリング応力とは？
薄肉で細長比が小さい断面を圧縮した場合に起こる、局部的な座屈現象をクリップリング破壊と言います。
クリップリング破壊は、圧縮部における板の部分が先ず荷重を取れなくなり、角部分が耐荷できなくなった時につぶれる現象です。
クリップリング応力は実験を元に算出される値であるため、計算方法が複数あります。本コラムでは最も広く利用されている、Lockeheed社のCrockettが発表した方法を紹介します。
クリップリング応力の算出方法
①平板要素への分割
例として、以下の様なT型断面におけるクリップリング応力を考えます。
クリップリング応力を算出する断面を、平板要素毎に分割します。
②平板要素毎のクリップリング応力の算出
①で分割した平板要素毎にクリップリング応力を算出します。
b/tが小さい領域ではFcyをカットオフ値とします。
また、「One Edge Free」と「No Edge Free」は、板要素毎の端部拘束条件を示します。T型断面の場合、全ての平板要素が片側しか拘束されていないため、「One Edge Free」となります。
この式は全ての延性材料に適用できます。
③断面全体のクリップリング応力の算出
例のように平板要素が複数ある場合は、下式のように平均値を断面のクリップリング応力とします。
④クラッド材の補正
クラッド材とは、板の表面に耐食性向上のための純アルミ層がある部材で、航空機の外板などに用いられる材料です。クラッド材はクラッド層の板厚分だけ強度が落ちるため、クラッド層を除いた板厚でクリップリング応力を計算します。
塑性座屈荷重
塑性座屈は、材料圧縮破壊とオイラー座屈の移行領域での破壊モードです。
材料圧縮破壊が発生する厚肉断面の軸力部材において、細長比が小さくなると塑性座屈が発生します。
塑性座屈荷重の算出式は以下になります。
また、応力で表すと以下となります。
塑性座屈荷重の算出には、圧縮ヤング率：Ecの代わりに接線剛性：Etが用いられ、Et以外はオイラー座屈の算出式と同じです。
接線剛性：Etは以下で算出されます。
ここで、Ec：圧縮ヤング率、n：Ramberg-Osgoodの数、F0.7：傾き0.7Eの直線と応力-ひずみ曲線の交点の応力値、Fc：塑性座屈応力、Fcy：圧縮降伏応力です。
接線剛性の計算式には塑性座屈応力：Fcが含まれるため、Fcの両辺がつり合うように収束させる必要があります。収束にはExcelのソルバー機能を用いることが一般的です。
その他の値は、航空機用金属データ集である、「Metallic Materials Properties Development and Standardization (MMPDS).」から参照します。
例として、7050-T7451 PLTの応力-ひずみ曲線を示します。
F0.7は上図のように、応力-ひずみ曲線から算出することも出来ます。
ジョンソンの座屈応力
ジョンソンの座屈応力は、クリップリング破壊とオイラー座屈の移行領域における薄肉断面の短柱領域の破壊モードです。クリップリング応力を使用するため、応力値で表されます。
ジョンソンの座屈領域は、長柱座屈領域であるオイラー座屈と繋がるため、2式を合わせてジョンソン-オイラーの式とも呼びます。
ジョンソン・オイラーの式はそれぞれ、以下になります。
[ジョンソン座屈応力]
[オイラー座屈応力]
細長比の値によって、どちらの式を使用するか判断します。
軸力部材の強度評価をしてみよう
以下の様な上下/左右対称なI型断面の両端単純支持された柱に、圧縮荷重が負荷された場合の強度を計算してみましょう。
なお、材料の許容値は航空機用金属データ集である、「Metallic Materials Properties Development and Standardization (MMPDS).」から参照した値です。
強度検討の順番は、①材料圧縮破壊、②クリップリング破壊、③ジョンソン・オイラー座屈破壊、④ねじれ座屈破壊、⑤塑性座屈破壊とし、安全率は1.5とします。
①材料圧縮破壊
断面特性値を算出します。y, z軸周りの断面二次モーメント、Iy, Izはそれぞれ下表の値となります。
圧縮応力：fは、負荷荷重を断面積で除した値であるため以下になります。
従って、材料圧縮破壊の安全余裕：M.S.1は、
となるため、材料圧縮破壊は問題ありません。
②クリップリング破壊
クリップリング応力を算出します。
平板要素①～④はOne Edge Free（m = 0.8, β=0.566）、⑤はNo Edge Free（m = 0.8, β=1.425）より、
[平板要素：①～④]
[平板要素：⑤]
[全体のクリップリング応力]
したがって、クリップリング破壊の安全余裕：M.S.2は、
となるため、クリップリング破壊は問題ありません。
③ジョンソン・オイラー座屈破壊
ジョンソン・オイラー座屈の閾値を比較します。
したがって、ジョンソン座屈応力：Fcr1を計算します。
したがって、ジョンソン・オイラー座屈破壊の安全余裕：M.S.3は、
となるため、ジョンソン・オイラー座屈破壊は問題ありません。
④ねじれ座屈
ねじれ係数：J、ワーピング定数：Γ、せん断中心まわりの断面の極慣性能率：Isをそれぞれ求めます。
したがって、ねじれ座屈荷重：PΦは、
したがって、ねじれ座屈の安全余裕：M.S.4は、
となり、ねじれ座屈破壊は問題ありません。
⑤塑性座屈応力
F0.7及びEtから、塑性座屈応力：Fcを算出します。
したがって、塑性座屈の安全余裕：M.S.5は、
となり、塑性座屈破壊は問題ありません。
①～⑤までの強度評価項目が全て問題ないため、この部材は強度的には問題ありません。
