投稿日:2021年10月25日

このコラムでは、エクセルを使ってH鋼の断面二次モーメントの計算方法をご紹介いたします。
エクセルを使った計算方法は、対象物を分割し「部位ごと」に求めていきます。そのため、H鋼のような単純形状から、複雑な形状までエクセル表の「行を追加」するだけで簡単に計算できる、という大きなメリットがあります。
具体的な計算方法を掲載していますので、最後までお読み頂きお仕事へお役立てください。
このコラムを書いた人

強度、振動解析の専門家
計算力学技術者(固体)、(振動)の1級を保有。航空機メーカーで10年、自動車メーカーで3年、それぞれ強度と振動の解析業務を担当する。現在は車載機メーカーで製品の強度・振動の保証業務の取りまとめ役。過去の経験や専門知識を活かして、悩める設計初心者に情報を発信する。趣味はサイクリング、2児の父として家庭と仕事の両立に日々邁進中。
断面二次モーメントとは?
さて、それでは断面二次モーメントとはなんでしょうか?ここで確認しておきましょう。
断面二次モーメントは、棒状の部材にモーメント(曲げる力)が発生する時の、「部材の曲げにくさ」を表す指標の一つで、単位は [mm4] です。

ご存知の方もいるかと思いますが、部材の曲げにくさを決める指標には以下の二つがあります。
・材料の曲げにくさ:ヤング率
・形状の曲げにくさ:断面二次モーメント
ヤング率は材料が持つ固有の値です。同じ形状を持つゴムよりも金属の方が変形しにくいのは、金属の方がゴムよりもヤング率が高いためです。

一方で断面二次モーメントは、モーメントが発生する断面形状によって決まる値です。
例えば、同じ材料でできた直径 10mm の丸棒よりも直径 20mm の丸棒の方が変形しにくいくいですよね。これは、直径 20mm の方が 10mm よりも断面二次モーメントが高いためです。
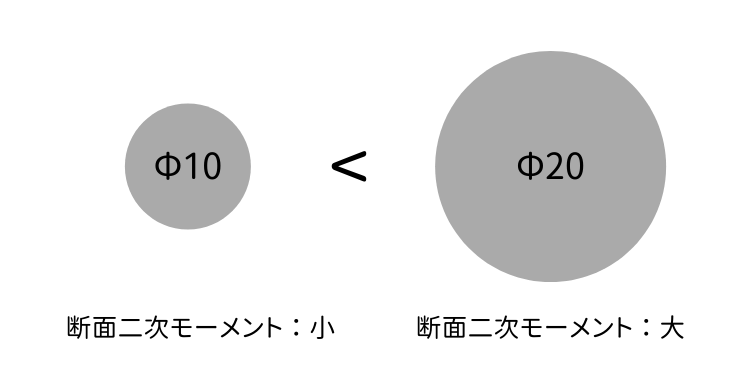
強度計算において断面二次モーメントは「部材の曲げ応力」を計算する際の必須知識です。ですが単位 [mm4] を見ただけで、その値が持つ意味を理解することは容易ではありません。
ですので、材料力学を学び始めたばかりの人は、まずは「断面二次モーメントは部材の曲げにくさを表す指標である」とだけ覚えておけば十分でしょう。
断面二次モーメントの公式と導出方法
●断面二次モーメント
実務では断面二次モーメントの公式を覚えておけば十分です。例えば、長方形の断面二次モーメント\(I_x \)の公式は、以下となります。
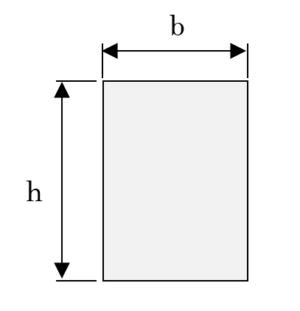
\(I_x=\frac{bh^3}{12} \)
ここではさらに、断面二次モーメントの理解を深めるために、この定義式から発展させた長方形断面の公式を導出してみましょう。
この先は少し内容が難しくなりますので、少し読み進めて「理解できないな」と感じた場合には、先に本ページ下部の「エクセルを使ったH鋼の断面二次モーメントの計算」をお読みいただき、あとから読み直していただいても大丈夫です。
それでは、説明を進めていきます。
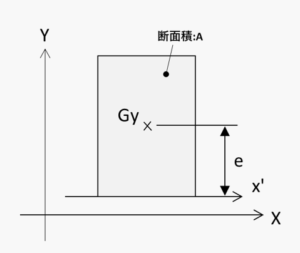
下図におけるx軸周りの断面二次モーメントIxの定義は、
\(I_x=\int y^2dA \) です。
\(I_x \) は図心におけるx軸周りの断面二次モーメントを、yは重心からの距離を示しています。また図のGyは断面形状の図心を表しています。
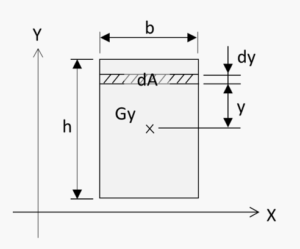
なお、y軸周りの断面二次モーメントはx、yの記号が逆になります。
この公式から、図心周りの長方形断面の断面二次モーメントを算出すると、
\(I_{xr}=\int y^2dA=\int_{-\frac{h}{2}}^{\frac{h}{2}}y^2 dA=\int_{-\frac{h}{2}}^{\frac{h}{2}}y^2bdy=2\times\left[\frac{y^3}{3} \right]_0^\frac{h}{2}=\frac{bh^3}{12} \)
となり、冒頭で紹介した公式と同じになります。
長方形断面の場合図心Gyは断面の中央になるため、積分範囲は0~h/2です。図心に対して対称形状なので、積分範囲を0~h/2で計算した断面二次モーメントを2倍した値が長方形断面の断面二次モーメントです。
●平行軸の定理
x軸とx’軸の距離をe、断面積をAとすると、x’軸周りの断面二次モーメント\(I_x’\)は、
\(I_x’=I_x+e^2A \)
となります。
平行軸の定理は複数の部材から構成される断面の断面二次モーメントを計算する時に使用します。H鋼は図のように複数の部材から構成されるので平行軸の定理を用いて計算します。

エクセルを使ったH鋼の断面二次モーメント
では実際にH鋼の断面二次モーメントを計算してみましょう。
続きを読むには…
このページは 会員限定です。申し訳ございませんがお客様の権限では続きをご覧頂くことができません。続きは、会員登録(無料)してご覧ください
個人・企業・学校等60,000人が登録
MONO塾の無料会員になると、サイト内にある人気コラムなどすべてのコンテンツが読み放題です。学習に役立つテキスト全18シリーズも無料でダウンロードいただけます。
会員の方はログイン