標準偏差、製造業で働く人にとって一度は聞いたことがある言葉ではないかと思います。でも、「標準偏差とは何なのか、どのように計算するのか、どういう場面で使われるのか」を知らない方もいらっしゃると思います。

今回は製造業で使われる標準偏差と公差の考え方について解説していきたいと思います。本記事を最後までお読みになれば標準偏差から寸法公差を決めるための概要が理解できるようになります。

標準偏差とは

標準偏差をひとことで言うと、データの平均値に対する偏差と確率を関連付けたものです。偏差を「σ（シグマ）」という単位で表現し、σで示す数値（平均値からの差）がデータ全体の何％に含まれるのか、を示したものです。

例えば、1000人の身長の測定データを集めたとします。データを整理した結果、平均値は160cmで標準偏差σは10cmでした。

ここで、標準偏差の決まりとして、平均値±σはデータ全体の68.27％を占めるという法則があります。

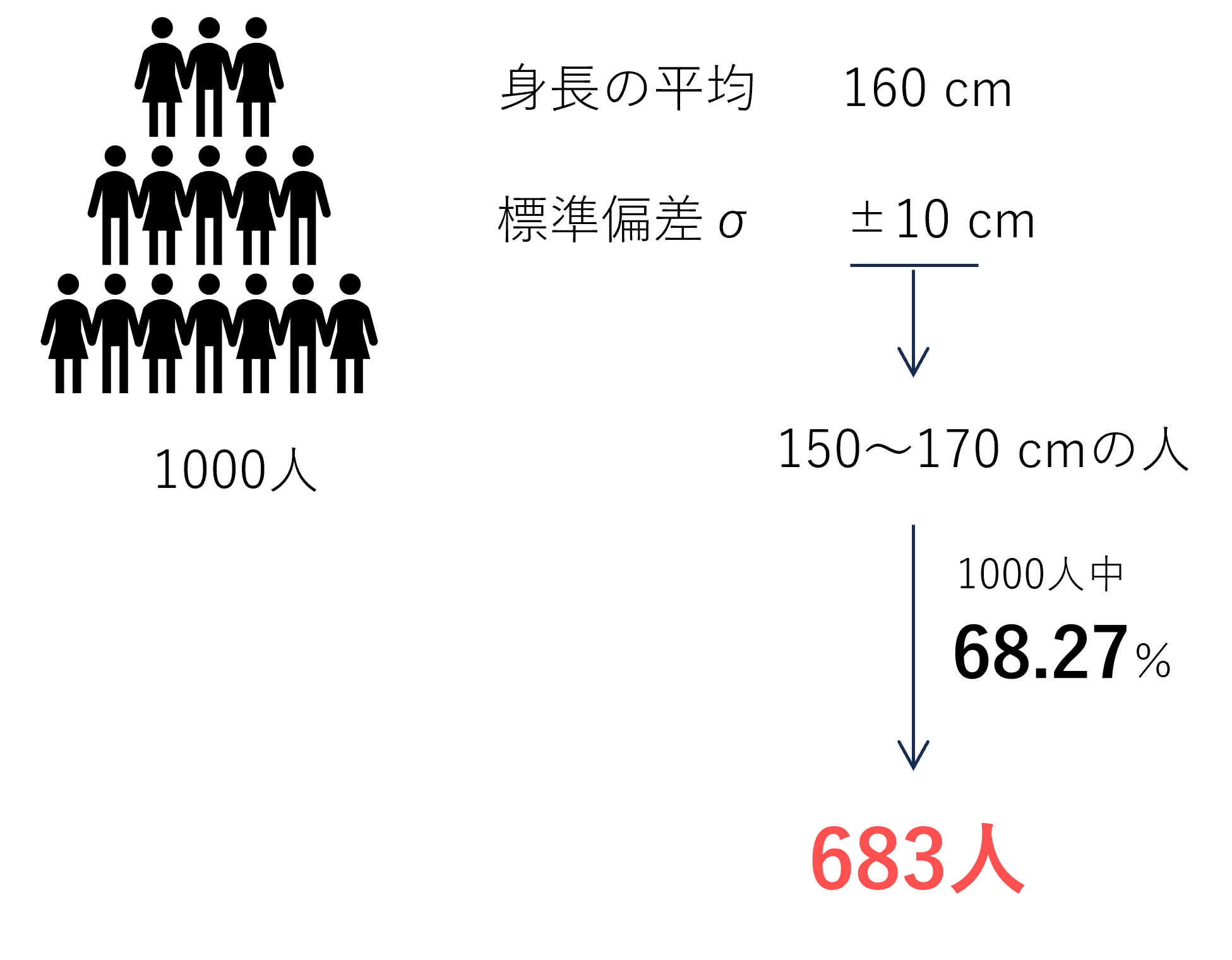
この法則から平均値から±10cm離れた領域(150cm～170cm)に含まれる人は683人ということになります。このようにしてσを計算することで、平均値の偏差が全体の何％を含むのかを理解することができます。

正規分布とは

標準偏差とは何か、について説明しましたが標準偏差をさらに理解するために正規分布について説明したいと思います。

図1のグラフは横軸が確率変数で縦軸が確率密度変数を示しています。グラフは釣がね状になっており中心は平均を示し、左右対称になっています。中心から離れたところは確率密度が少なくなっていることがわかります。

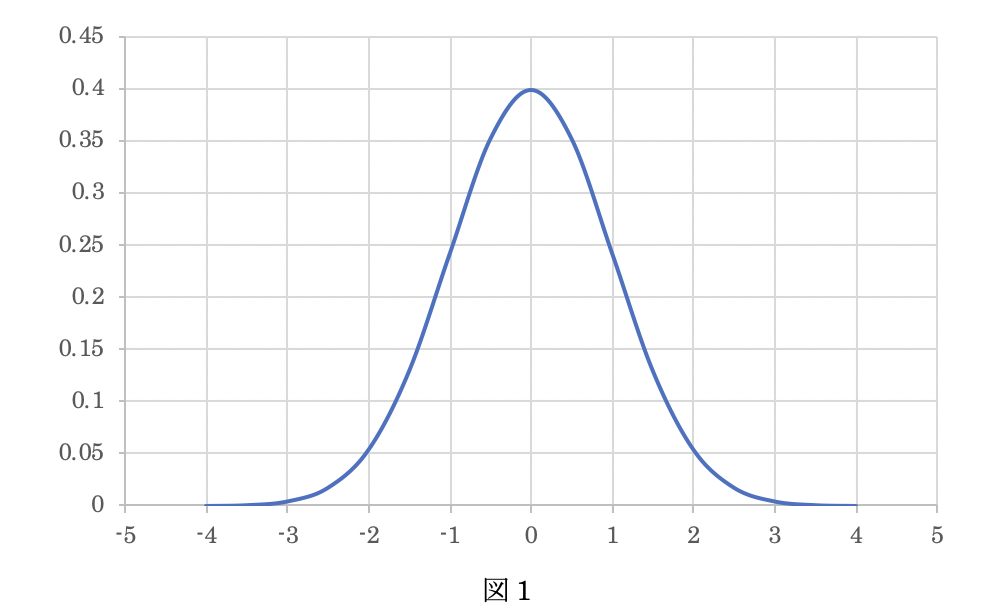
この分布を正規分布と呼び、以下の確率密度関数の式で表すことができます。

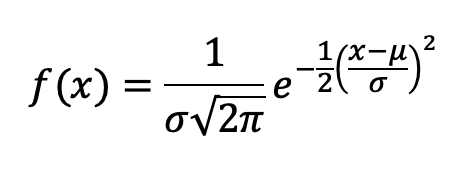
σ：標準偏差
μ：確率変数の平均
ｘ：確率変数

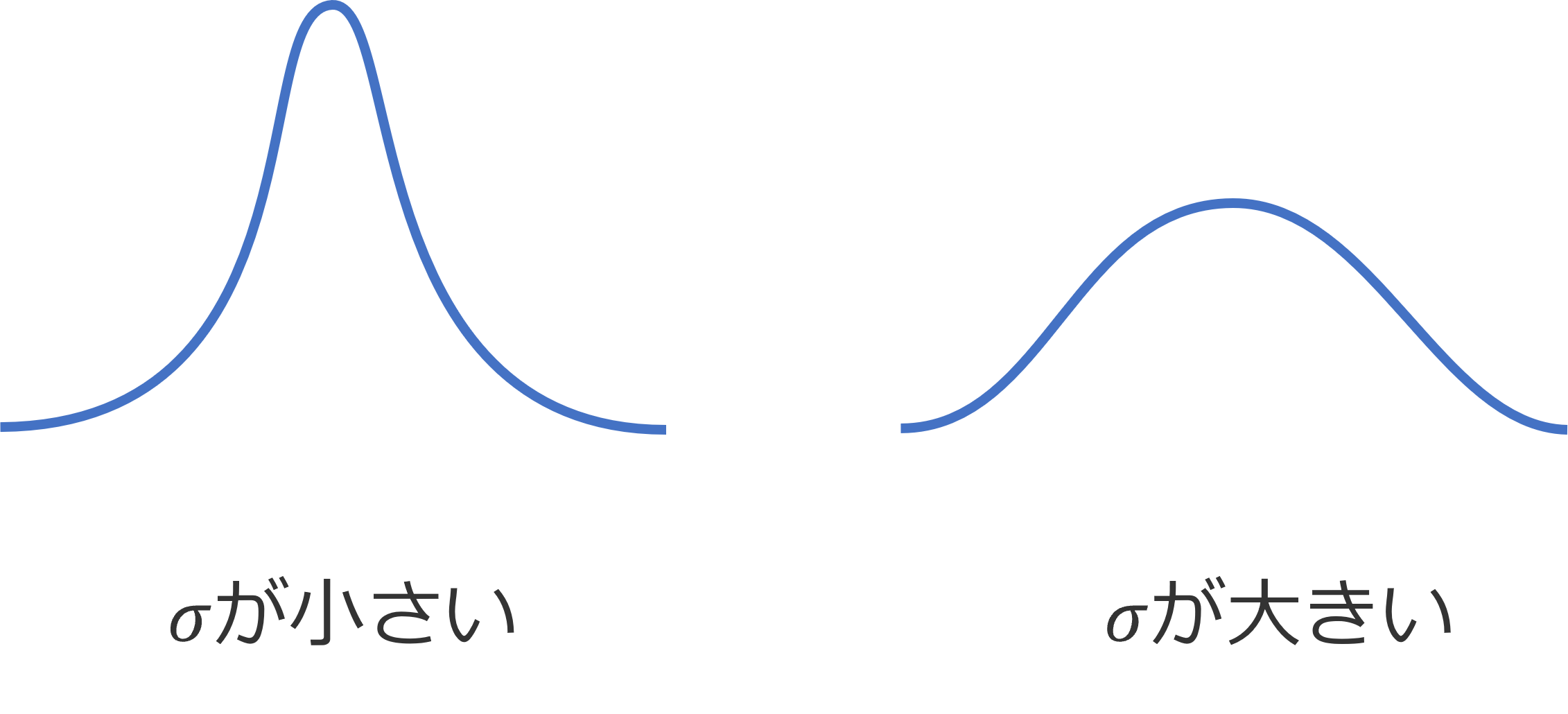
σが小さくなれば図1の山が鋭い形状になって、σが大きいとなだらかな形状になります。

ここで、全ての事象が必ず正規分布に従うのか？という疑問が生じてくると思います。これに関しては、「データはあくまでも正規分布に従うと仮定しているだけ」であり、世の中全てのデータが必ずしも正規分布になることはない、と意識しておくとよいでしょう。

取得したサンプルによってはほぼ一様分布になる場合もあります。ただ、一般的な統計学手法として多くの分野で正規分布が使われています。

ここで標準偏差の話に戻しましょう。正規分布と標準偏差がどのように関わっているかということについて説明します。

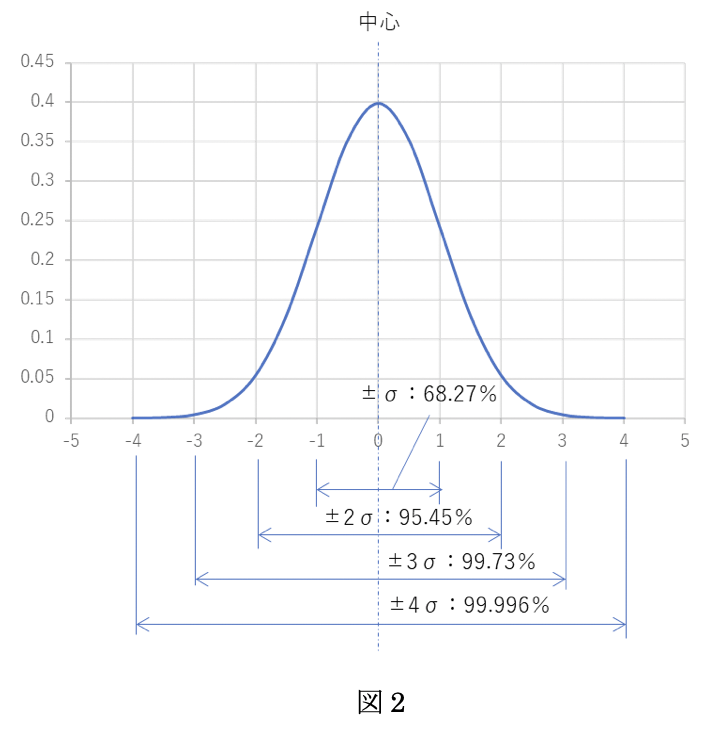
図2は図1にσの範囲を追記したものです。

σは正規分布の区間を示しており、正規分布のグラフで形成される面積100％とすると±1σは68.27％、±2σは95.45％、±3σは99.73％の面積を示しています。

面積100％はデータ母集団（または標本数）の合計値です。このようにσを増やしていくとデータ全体に占める標本数の確率が大きくなります。ちなみに先ほど説明した確率密度関数の式から計算してみると5σ、6σ…と、どんなにσを増やしても100％に届かないことがわかります。

標準偏差が使われる場面

標準偏差（σ）は次のような場面で使われることがあります。

品質管理

製造業では、部品の寸法値や製品の性能など、さまざまな検査項目があり、規格値があります。

例えば、出荷検査で電流値を測定するときに、40±4Ａという基準があった場合、36～44Ａであれば合格、それ以外であれば不合格となります。この基準を決める根拠としては、製品の性能や機能に影響しない範囲で決めたり、電流値のばらつきによって決めたりします。

電流値のばらつきで決める場合は、事前に集めた個体毎の電流値のばらつきから、標準偏差を求め、規格値を決めます。

先ほどの例で、電流値のばらつきが正規分布に従うと仮定した上で、σ＝1Ａの場合、4Ａは4σになります。±4σは99.994％、10万台中6台が不合格になる確率です。もし対象台数が1万台であれば不合格が発生しない、という見方ができます。（あくまでも正規分布に従えばという仮定です。）

偏差値

学校の成績で良く聞く言葉ではないでしょうか。

偏差値30よりも80の学力が良いことはすぐわかると思います。偏差値は「（個人の特定-平均値）÷標準偏差×10＋50で計算します。このように偏差値も正規分布を基準にしており、個人の得点と平均値、標準偏差から算出します。

偏差値50であれば全体の50％、偏差値80％であれば全体の0.13％に相当します。

標準偏差を計算してみよう

全てデータがある場合と、一部のデータしかない場合

これまでσと言ってきましたが、実は「σ」と言えるのはデータが全て揃っていて母集団と言える場合です。一部の標本数を基に標準偏差を推定する場合は「s」で示します。σとｓはそれぞれ、次の式で表します。

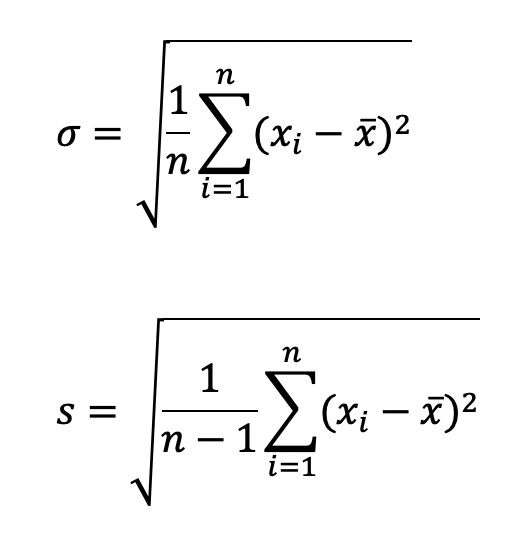
製造業で規格値を決める場合において、一部のサンプル数を基にこれから発生するのであろうばらつきを予測していく手法をとるときは、「s」を計算したほうが良い場合もあります。

標準偏差はエクセルで計算できる

標準偏差を式で求めるのは大変です。そこで、エクセルを活用して算出する方法を説明します。

エクセルでは、以下の関数を使って標準偏差を求めます。母集団から標準偏差を求める場合と標本から標準偏差を予測する2種類を紹介します。

STDEV.P関数：選択したセルの範囲を「母集団」とみなし、標準偏差を計算する。
＝STDEV.P（数値範囲）

STDEV.S関数：選択したセルの範囲を「標本」とみなし、標準偏差を計算する。
=STDEV.S(数値範囲)

標準偏差から公差を決める

その公差は何σ？

公差とはある寸法に対する許容幅のことです。例えば棒の長さを100mm毎にカットする場合、図面に記入する長さ寸法は「100」ですが、実際は99.99mmや100.02mmなど、完全に100mmに一致させることは不可能です。そこで100±0.1などの「許容幅」を設けます。

公差を厳しくすると管理が難しくなる、と言われています。同じ寸法公差でも実際のばらつきが少ない、すなわち標準偏差が小さくなる分、不合格率は減りますが著しく公差を厳しくすると、不合格の数量が増え、経済上よくありません。

そこで、JISで規定されている公差を採用します。図面に公差を記載していない場合、JISで規定された公差にしたがって製品を作ります。しかし満たすべき機能を満足させるために一般公差よりも厳しくしなければいけない場合があります。

この時、製品のばらつきから標準偏差を求めて、公差を決める方法があります。

公差は一般的に±3σや±4σの幅にするという話を聞いたことがあります。もし±1σの幅しかなければ31.7％が不良品になってしまいますが、±4σであれば不良率は0.006％まで減ります。
このように標準偏差を活用して、製品の機能面、歩留まり、品質検査の工数などを考慮して公差を決めていきましょう。

必要なデータ数

標準偏差を予測するための必要最小限のデータ数は一概に言えないところがあります。データが多ければ多いほど正規分布に近づくため、データ数は大きいことに越したことがないからです。
ただし、サンプル数の都合で、取得できるデータ数に限りがあるのは確かです。

もし所属している部署で経験的にどの程度サンプル数があれば良いか聞いてみて、それに従うのもいいでしょう。また、継続的にデータの取得が可能であれば、最初は少ないサンプル数で仮の標準偏差と管理値を決めておいて、継続的に見直すのも良いでしょう。

組み合わせる部品の公差を考える

前項では1つの寸法に対するばらつき例を説明しましたが、製造業で検査する管理値には複数の部品が組み合わさったものも多いため、この管理値を満足するために1つ1つの部品にどのように公差を割り振っていけば良いかわからないこともあると思います。

既製品の部品の公差を1つずつ積み上げてみると、製品の規格値を満足しないことに気づくはずです。

これは確率で考えると納得がいきます。製品が5つの部品で構成されていると仮定して、部品の公差が全て3σでできているとします。これを5部品全て3σで積み上げてしまうと、製品の規格値は合計で3σの確率の5乗となり過剰品質となるのです。

この問題を解決する方法として二乗平均やモンテカルロ法という方法があります。

これは、部品の組合せを確率が最も少ない同士の組合せとするのではなく、一つの部品がたまたま公差上限または下限値で作られたとしても、組合せる部品はそうはならないと考える方法です。

二乗平均は公差中央値との偏差を2乗したものを平均した値に対して平方根を取る方法です。

モンテカルロ法は乱数を使う計算手法です。今回の場合ではそれぞれの部品の乱数を生成し、それぞれを足した合計の標準偏差が製品の標準偏差になります。
このように二乗平均やモンテカルロ法を使用することで公差を単純に足し算した場合よりも累積公差を小さくすることができます。

まとめ

今回は以下について説明しました。標準偏差は品質管理に必要な規格値を決めるためになくてはならないものです。データから標準偏差を求めて効率良く活用していきましょう。

1. 標準偏差はσまたはｓで表す。σは母集団を対象にした標準偏差でｓは標本から標準偏差を予測したもの
2. ±1σは68.27％、±2σは95.45％、±3σは99.73％の確率を占める
3. 標準偏差はエクセルで求められる。(STDEV.P関数またはSTDEV.S関数)
4. 公差と標準偏差の関係を確認する。（その公差は何σか？）
5. 組み合わせる部品の公差を考える際は、二乗平均やモンテカルロ法を使用する場合がある