現在の製品開発においてCAE(Computer Aided Engineering)は、強度評価の際に欠かすことの出来ないツールになっています。

その中でも、設計者が強度評価に利用するCAEツールは、有限要素法(FEM: Finite Element Method)の「線形解析」が使われている場合がほとんどですが、解析専任者でなければ、計算理論までを意識して使っている人は少ないのではないでしょうか？

このコラムでは、線形解析と非線形解析の違いや、非線形解析を用いる場合などを解説します。強度評価をする際にCAEツールを使っている人で、線形・非線形をあまり意識していない方は、ぜひ自分の業務と照らし合わせてみて下さい。

線形解析と非線形解析の違い

「線形」とは、ある値「a」とある値「b」が比例する関係のことを示します。

構造解析において「線形解析」とは、負荷した「荷重」と部材の「変位量」が比例する解析のことを指します。

では線形解析と非線形解析の違いを、FEMで用いる数式を用いて比較してみましょう。

線形解析において、各接点における荷重：Fと変位量：Uの関係式は構造物の剛性：Kを含めて以下で表されます。

{F}=[K]∙[U]

FEMにおいて構造物は複数の接点で構成されるため、関係式は行列式となります。

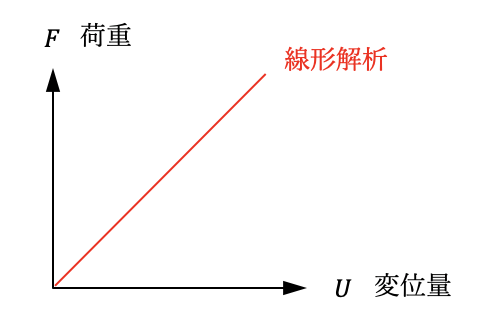
上式で示す通り、線形解析では剛性：Kの値が一定のため、荷重と変位量は比例します。

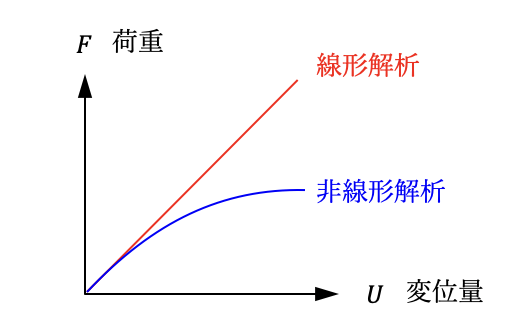
一方で「非線形解析」における荷重と変位量の関係式は以下で表されます。

{F}=[Kt(U)]∙[U]

非線形解析では剛性：Kt(U)の値が変位量によって変化するため、荷重と変位量の関係は比例しません。

線形解析では荷重と変位量の関係が比例するため、荷重を負荷する前のつり合い状態における行列式を一度だけ計算すれば解を出すことが出来ます。

しかし、非線形解析では変位量によって剛性値が異なるため、変形する度につり合い状態を何度も計算する必要があり、線形解析に比べると計算時間が長くなります。

非線形解析の方が線形解析よりも、実現象をより詳細にシミュレーションすることが可能ですが、製品開発の現場では計算コストを踏まえて、非線形現象を無視できない場合以外の「微小変形領域」では線形解析を用いることが一般的です。

材料非線形

弾塑性挙動

金属材料に見られる、典型的な材料の非線形性の一つが弾塑性挙動です。

下図は軟鋼の応力とひずみの関係を示しています。部材に荷重が負荷されると、弾性変形領域ではヤング率：Eの傾きで、応力：σとひずみ：εの関係は線形となります。

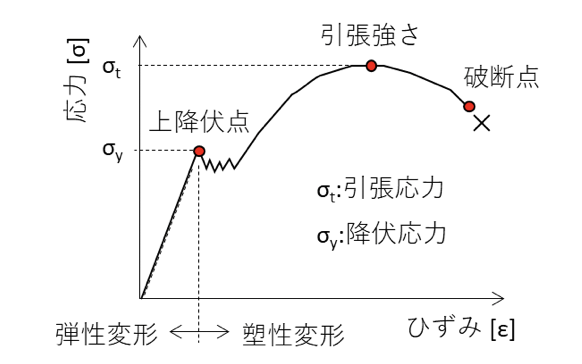
しかし、荷重が大きくなり応力が降伏応力：σy以上となると、塑性変形領域となり非線形となります。

塑性変形領域で線形解析を行うと、応力値が過大に、変形量が過少に計算されてしまいます。

下図に塑性変形領域における線形解析のひずみと応力の関係を示します。

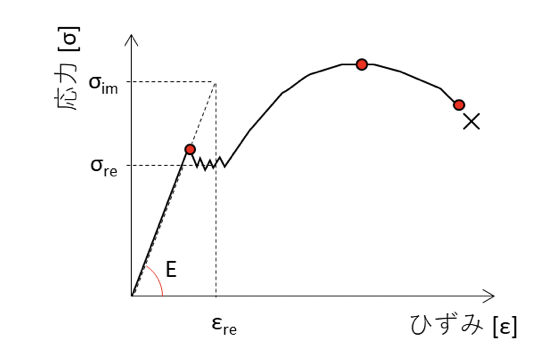
塑性変形領域においてひずみ：εreが生じた場合、線形解析を用いると応力集中部に応力：σimが発生します。

しかし弾塑性挙動を考慮すると、降伏点（σre）以降で非線形となり、弾性変形領域よりも荷重に対するひずみ（変形）が大きくなるため、応力集中部でとれない荷重が応力集中部の周りに再分配されます。

すると、非線形解析では線形解析よりも最大応力値は小さくなりますが、塑性変形領域が広くなるため変形量が大きくなります。

超弾性挙動（ゴム）

弾性変形なのに応力とひずみが非線形となる材料を、超弾性材料といいます。

ゴムは典型的な超弾性材料として扱われます。ゴムの応力とひずみの関係は下図に示すようにS字カーブ状となり、荷重負荷時も除荷時も同じ曲線をたどる材料としてモデル化されます。

圧縮時の応力とひずみの関係が引張時と異なるのも、ゴムの特徴の一つです。

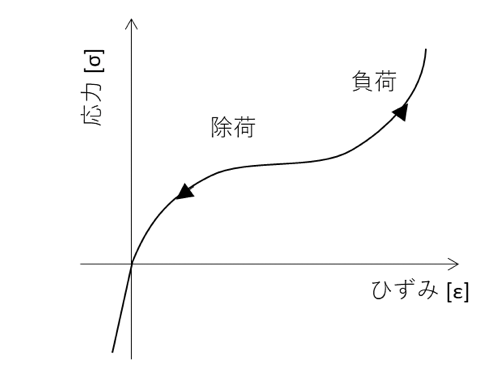
ゴムの解析では、後述する「幾何学的非線形性（大変形）」や「境界条件非線形（接触）」等の非線形性も考慮する必要があるため、専門的な解析手法の知識が必須な、初心者が扱うには注意が必要となる材料です。

幾何学非線形

部材に荷重を負荷すると部材は変形しますが、変形や応力の発生によって部材の剛性が変化することを「幾何学非線形」といいます。

幾何学非線形は、変形量が大きくなるために、変形前後の荷重のつり合い状態が異なることが原因で非線形となる「大変形問題」と、部材の形状によってある応力以上の負荷応力が発生することで部材形状が突然変化する「座屈問題」があります。

座屈問題の例として、下図のような浅いアーチ型の形状を持つ部材の中央に荷重を負荷した場合を考えます。

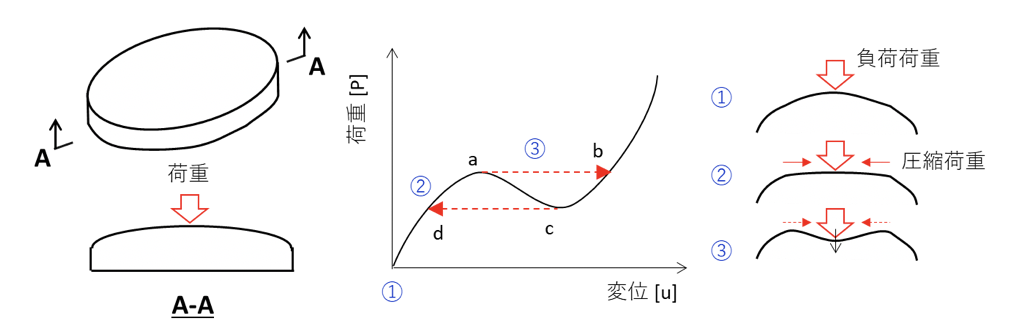
中央部に荷重を負荷して変形が生じると、面内方向に圧縮荷重が発生します。さらに変形を大きくしていくと、ある点で中央部の下向きの圧縮荷重に部材の剛性が耐えられなくなることで、突然下向きに大きな変形が起こります（図中a ⇒ b）。

上記の現象を、「飛び移り座屈」といい、除荷の場合でも同様に非線形挙動を示します（図中c ⇒d）。

境界条件非線形

FEMにおいて「荷重条件」と「拘束条件」を合わせて「境界条件」といいます。境界条件非線形は、接触や摩擦・荷重ベクトルの変化などにより、境界条件が非線形となる現象です。

境界条件非線形の主なものに物体の接触現象があげられます。以下に球形のゴムを、固い床に押し付けた場合を考えます。

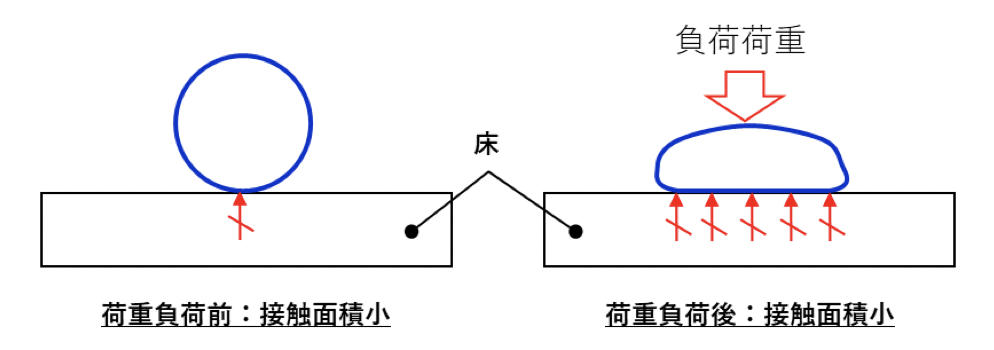
荷重が負荷されていないときは、ゴムの変形はほとんど無いため、床からの反力は非常に狭い範囲で受けます。

しかし荷重が負荷されて変形が大きくなるにつれ、ゴムが床に接触する面積が大きくなり、反力を受ける範囲も大きくなるため、境界条件が変化します。

このような接触を含む解析を行う場合には、非線形性の考慮が必要になります。

非線形解析を用いる事例

今まで紹介した非線形解析は特殊な材料や条件が前提であるため、フックの法則が成立する金属材料であり、変形が小さい「微小変形領域」であれば、線形解析でもある程度の精度は確保されます。

しかし変形が小さい場合でも、実現象との誤差を考慮する必要がある形状があります。それは下図に示すような、平板に面外荷重を負荷した場合です。

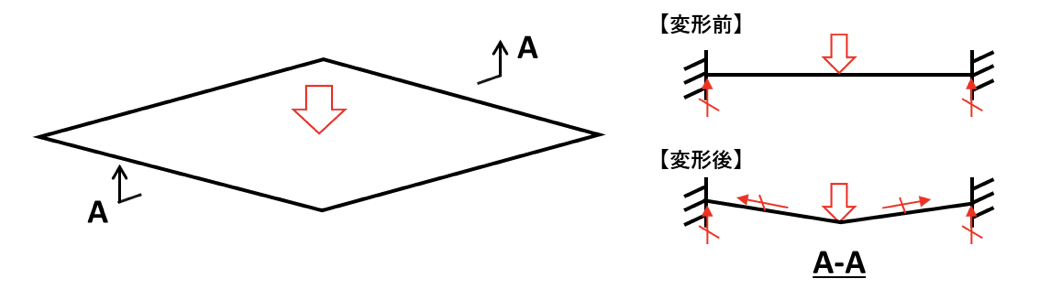
図のように平板の中央に荷重を負荷すると、中央の変形量が増えるにつれて平板を引っ張るように面内方向の反力が発生します。

しかし線形解析では、変形前の荷重のつり合い状態を元に変形量を計算するため、平板の面外方向の剛性しか考慮されず、実現象よりも変形量が大きく計算されてしまいます。

車や航空機の床面や燃料タンクなどの部品でも同様です。

このような部材の解析では、線形か非線形かは計算結果に大きな差が出る場合があるため、変形後の形状を想像しながら解析をすることが重要です。

• CAEを学ぶ