前回のコラムでは、振動の基礎として、

• 振動が人体に及ぼす影響
• 振動が製品に及ぼす影響
• 自由振動、強制振動などの振動の種類

などを解説いたしました。

前回のコラムをまだお読みいただいていない場合はこちらからご覧ください。

本コラムでは、振動現象の基礎である変位、速度、加速度の関係性について解説します。

振動の力学モデルと物体の性質

振動を測定するにあたっては、変位、速度、加速度の３つの基本的性質を把握することが出発点となります。

そして、変位、速度、加速度に対して、それぞれ慣性力、粘性抵抗力、復元力という力が反対向き発生し、これらを物体が持つ基本性質といいます。

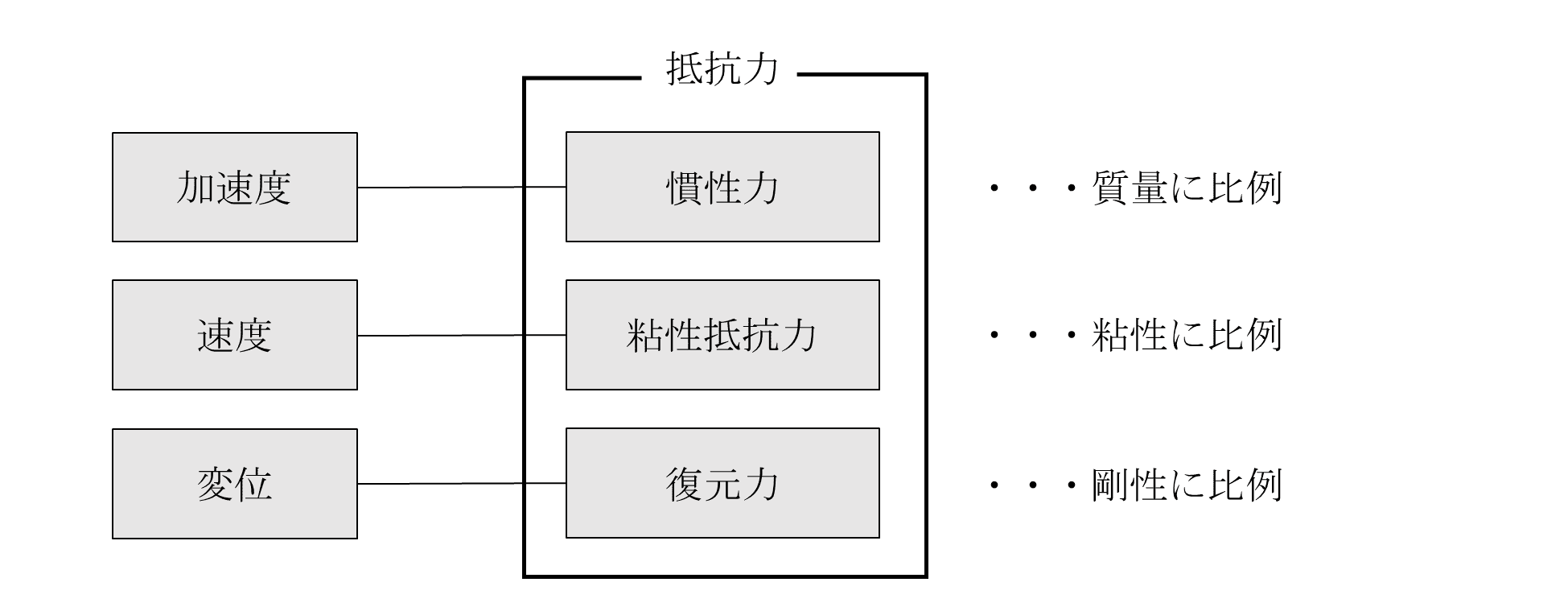
これらの抵抗力は物体自体の動特性である、質量、粘性、剛性の3種類の性質にそれぞれ比例します。

また、これらの基本的性質は、質量、粘性、剛性の3種類の性質にそれぞれ比例します。例えば、自動車で説明すると、車両重量（質量）が軽くなれば、加速度が上がる、粘性（例：空気抵抗）が小さければ、速度があがります。

さて、振動を考えるとき、下図のような力学モデルで考えることが多くなります。

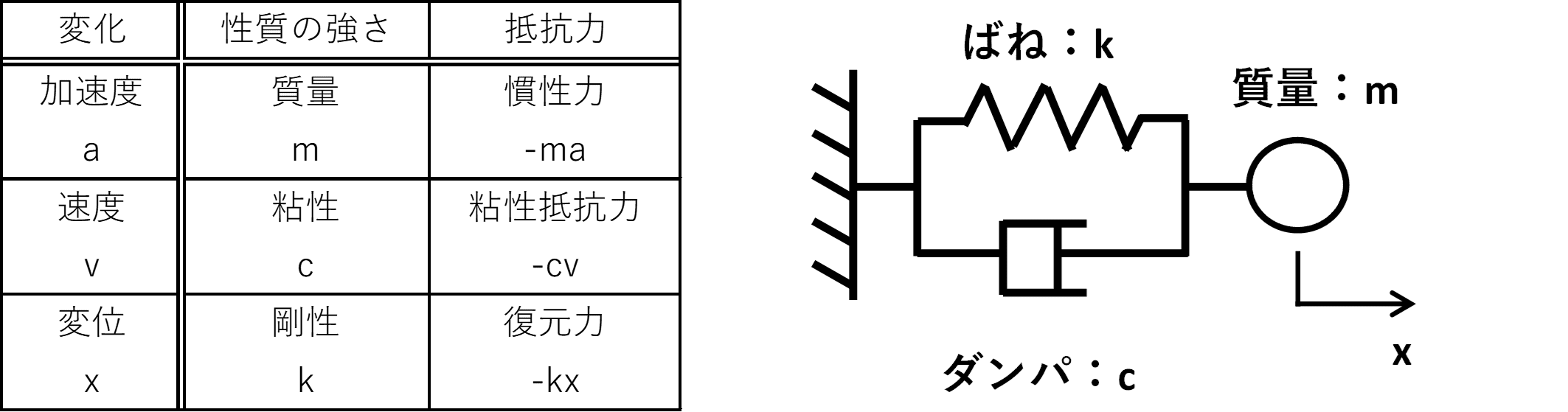
力学モデルでは質量は丸い固まり(m)、粘性をダンパ(c)、剛性をばね(k)として表現しています。

この力学モデルは、振動系内に動特性がそれぞれ1つずつ表現されているため、「1自由度系のモデル」と呼ばれ、振動を考える上で最も基礎的なモデルとなります。

なお、外部の振動がない1自由度力学モデルにおける運動方程式は、以下になります。

なお強制振動を表す式では、右辺の0がF(t)となります。

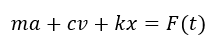
この運動している時の力のつり合い式が、振動現象を考える上での最も基礎的な関数となります。

不減衰1自由度モデルにおける自由振動

先に紹介した運動方程式において粘性力は全ての振動を抑制する働きをするもので、振動を減衰させて止めてしまうものです。そのため粘性抵抗力を粘性減衰力ともいいます。

振動現象を把握するには粘性は省略する方が分かりやすいため、下図のように減衰を省いた「不減衰1自由度モデル」における自由振動を対象に振動現象を考えてみましょう。

以下に不減衰1自由度モデルの力学モデルの運動方程式、及び変位の式を示します。

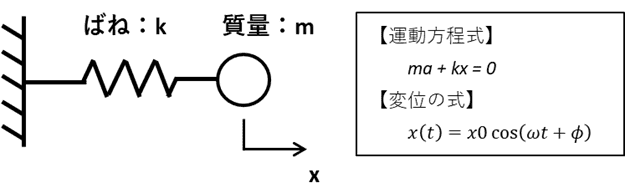
変位の式は運動方程式を解くことで導出される式です。式における、x0、ωt+φ、φはそれぞれ、振幅、位相、初期位相を示しています。

振幅は質量が動く範囲を、位相は振動している部分が他の部分に対する位置関係をそれぞれ表すパラメータです。

では変位の式「x(t)=x0cos(ωt+Φ)」が意味する運動をイメージしやすいように図示してみましょう。

下図はバネにつるしたおもりを静止状態から下にx0引っ張って手を離した時の変位を示しています。手を離した時をt=0としています。

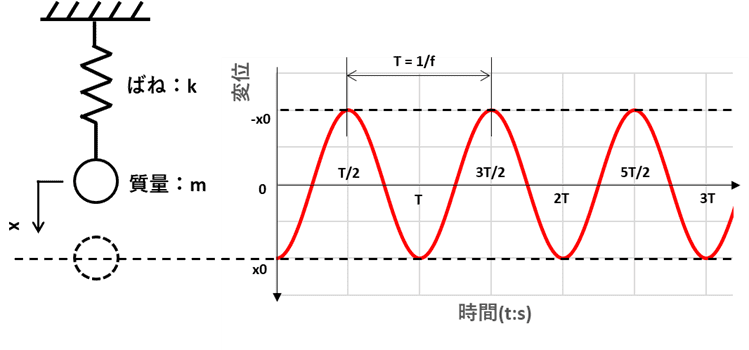
おもりから手を離すと、バネの力によって変位は-x0まで上昇し、その後x0と-x0を往復する運動を繰り返します。

質量の変位量:x(t)は横軸を時間とすると、上図のようにコサイン波形を描くようになります。

コサイン波形で表される変位量：x(t)は1周期：T(s)が2π(rad：2π=360°)となる振動です。

そのためωT=2πとなり、1秒間の振動する回数をf（振動数：回/s）とすると、ω=2πfとなります。これは時間2πの間に振動する回数を示しています。

ちなみに、運動方程式から角振動数：ωを解くと、

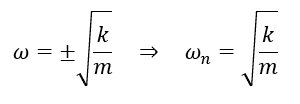
となりますが、この時のωnを固有角振動数と言います。

固有振動数は系の内部の抵抗力（最初の式の左辺）が0となる時の振動数を表しているため、固有角振動数の振動数を持つ力が外部から加わると振動し続けることになります。この現象が共振です。

変位、速度、加速度の変換方法

速度、加速度は変位を、時間：tでそれぞれ1階微分、2階微分すると求められます。変位は、

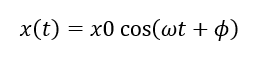
であるため、速度、加速度はそれぞれ、

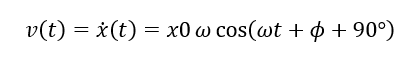
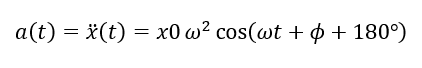
となり速度、加速度の位相は変位からそれぞれ、90°、180°遅れるようになります。

位相が遅れるという感覚は、数式だけではイメージしづらいため、下図のように力学モデルを用いてその現象を順に見ていきましょう。

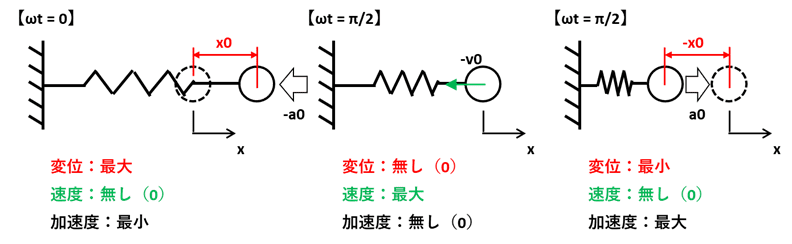
図は各位相におけるおもりの変位、速度、加速度をそれぞれ表しています。

おもりをx0引っ張った時をスタート（ωt=0）とします。

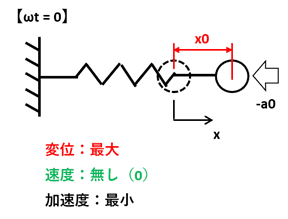
スタート地点では変位量はx0となり最大値を示します。一方で、手を離した瞬間の速度は無いので0です。また加速度はバネが縮もうとする方向に働くため、スタート地点では最小（マイナス）となります。

なお加速度はバネの伸び・縮み量に比例するため、変位量とは逆方向に働きます。これを位相で考えると180°ずれていると表現されます。

次に位相がπ/2（90°）進んだ場合を考えてみます。

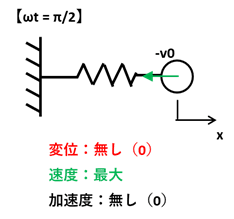
位相がπ/2の瞬間の変位量は0となります。またこの瞬間は、バネの伸び・縮み量が0となるため加速度も0になります。一方で変位量が0となる時、速度は最大となります。

これは加速度が常に変位量と反対方向に働いている（ブレーキをかける方向に働く）ためです。

次に位相がπ（180°）の瞬間を考えてみます。

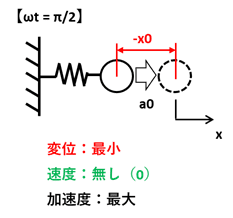
位相がπの瞬間の変位量は-x0となり、最小値となります。またこの時はバネの縮み量が最大となるため、加速度は最大値であるa0となります。一方で、おもりが停止する瞬間であるため速度は0となります。

振動はこの運動を繰り返します。変位、速度、加速度を図示すると下図のようになります。

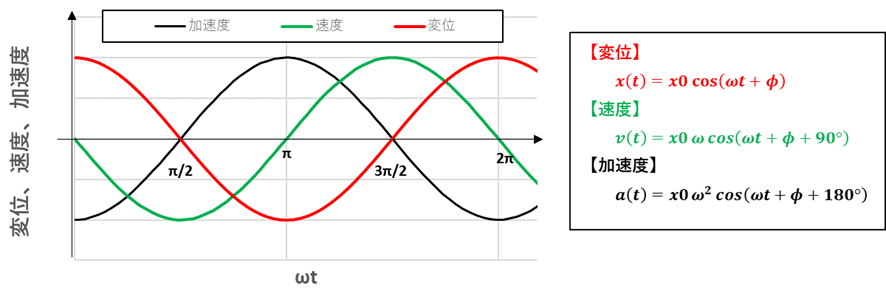
グラフから速度、変位はそれぞれ加速度から90°(π/2)、180°(π)遅れて現れていることが分かります。

以上、本コラムでは、振動現象の基礎である変位、速度、加速度の関係性について解説してきました。これらの内容は振動問題を扱ううえで理解しておかなければならない基礎的な知識になりますので、しっかりと理解しておきましょう。

• 機械力学を学ぶ