「熱媒配管を更新した後に、熱媒油を通したところ、急に激しい音とともに配管固定金具が破壊されてまった」

「まっすぐにつないだ配管に蒸気を流したところ、配管が伸びてしまい周囲の構造物に干渉し破壊してしまった」

金属材料は耐熱性が高い半面、熱膨張をしてしまう材料であるため、正しく膨張量を把握しておく必要があります。

特に、熱膨張は全方向に対して伸びるため、大型になればなるほど、比例して大きく伸びてしまいます。

その中でも、配管のような長い距離をつなぐモノは、その軸方向の長さに対して、熱膨張が起きてしまう為、想定外の変位が生じることになるのです。

その為、装置ユニット内に熱媒配管を這わせたり、長距離の蒸気配管を敷設する時に、熱応力についてしっかりと検討をしておく必要があります。

熱応力とは？

ここで、配管に生じる熱応力とは何かについて説明をしておきます。

熱応力とは、配管が熱膨張を起こそうとする力に対して抵抗する応力を指します。熱応力は主に、その配管を支持（拘束）している部分で生じます。

その拘束する応力が、どのように発生するかはなかなかイメージしづらいかと思います。
そんな時は以下のように考えると分かりやすいかもしれません。

真っ直ぐな配管の両端を拘束して固定した状態で、配管を加熱するとその両端に受ける応力は、配管両側を自由にして、加熱し、熱膨張させ、その状態から両端に圧力をかけて元の長さにまで戻す応力と同じと思えば良いです。

熱応力はどう計算するか？

熱による伸び量が「歪み（ひずみ）」であると捉えると、その歪みを生じさせる応力は

歪み応力σ=ヤング率E×️歪み長さ⊿÷全長L で計算できます。

さらに、歪み長さ⊿は、熱膨張で伸びた量と同じであると考えると、

歪み長さ=熱膨張伸び長さ= 線膨張係数Ｃ×全長L×温度差dt で計算できるため、

熱応力

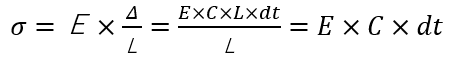
となります。

線膨張係数Cについては以下の表を参考にしてみてください。

各温度における代表的金属の膨張係数(×10-6)

温度範囲	0~100℃	100~200℃	200～300℃
アルミニウム	24	24.7	25
銅	16.6	16.9	17.3
鋳鉄	10.4	11	11.7
炭素鋼	11.5	11.9	12.6
ステンレス鋼	16.7	17.2	17.6

感覚的に1mの配管に熱を加え、温度差100℃を生じた際に、アルミパイプは2mm、鋼製パイプは1㎜熱膨張が起きると考えるのが一般的とされています。

この考え方を使って例えば、100mの鋼製配管に180℃の温度の流体を流す際にどれくらい熱膨張するか（流す前は30℃）を考えてみます。

以下の様に考えてみましょう。概算の熱膨張量がすぐに分かるようになります。

[全長]100m×[鋼製配管なので]1（mm/m℃）×[温度差](180℃-30℃)÷[基準温度]100℃=150mm

となり、配管の長さが150mm程度熱膨張することになります。

配管が長ければ長いほど、決して無視できない大きな値になるので注意が必要です。

さらにこの変位を伸びない様に固定してしまうと、その固定部では、先ほどの計算では、おおよそ340MPa※の応力が一方向に負荷することになるのです。

※これは一例ですが、配管断面積次第で、数十t～数百t以上の大きな力がかかることになります。

配管指示部で配管から熱応力を受けるのを恐れて、全く固定部を設けずに設計してしまうと、その応力は、代わりに配管を繋いでいる機器ノズルに作用する事になり、機器の破損を招いてしまいます。

では配管設計はどのように考えればよいか？

熱応力がどれくらいの大きな応力になるのかイメージを持ってもらった所で、実際に配管をどの様に設計すべきかを説明していきます。

配管を設計するポイントは以下の2つです。

1. 配管の固定箇所（変位０箇所）を決めて、そのほかの固定箇所は、伸びを許容できる配管固定法にする。
2. 配管自体に伸縮性を持たせる。

➀伸びを許容出来るような配管固定を行う

配管の熱膨張に合わせて指示部がスライドするような設計を行い、固定部に応力が集中するのを防止する方法です。スライド面の面摩擦をなくすことで、配管の固定部への応力を減らすことが出来ます。

とはいえ、一切の固定箇所（配管の変位）が無い場合は、その配管の両端にある機器ノズルに大部分の応力が伝わることになる為、固定箇所はどこかに必ず必要となります。

スライドできるサポートの形状としては、以下のようなシンプルな形状で良いかと思います。

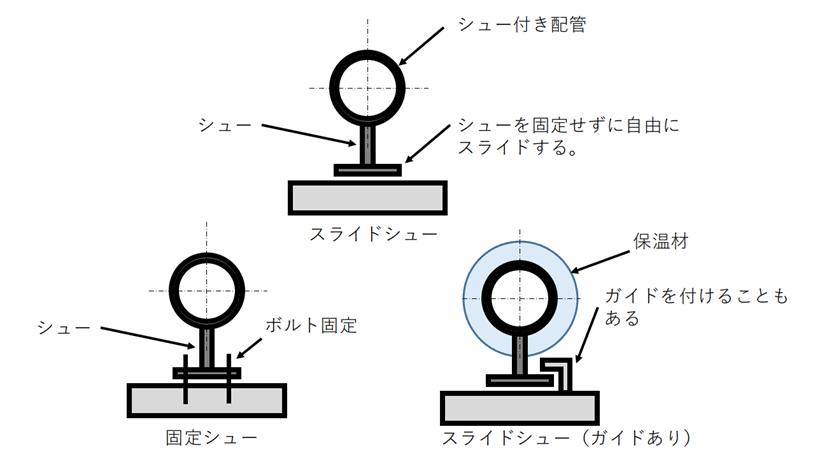
配管固定・配管支持方法の例（断面模式図）

（小径配管はよりシンプルに、Uバンドのみで固定しても十分スライドする）

➁配管自体に伸縮性を持たせる

配管がばねのように伸縮すれば、熱膨張した変位を吸収することが出来ます。

伸縮性のある継手（伸縮継手やヒンジ継手）を用いて変位の吸収を行うことも可能です。
ただし吸収できる変位に限界があるため、事前にどの程度の変位が生じるかを計算しておく必要があります。

ちなみに、一つの継手で吸収できる膨張長さを「トラバース」と呼びます。

伸縮継手もメーカによって様々な形状がある為、メーカに問い合わせする際は簡単な配管ルートと仕様条件（圧力・温度）を連絡してみましょう。

伸縮継手の種類

又、配管自体に伸縮性を持たせ、熱膨張分の伸びを吸収出来るように曲げ管を用いる方法もあります。工場内等の配管では、配管を通す場所が十分に確保されている為、この手法が一般的となっています。（この記事の最後に手法を紹介しています）

まとめ

熱応力は配管に熱を与えれば簡単に発生してしまう半面、配管固定部に想像以上に、大きな応力が発生してしまう可能性があります。

高温の配管をユニット内に組み込む際や長距離の配管を敷設する際は、配管の熱膨張の検討を忘れずにしておくようにしましょう。

以下補足として、配管自体に伸縮性を持たせる為の計算方法について紹介します。手計算でもできるので現場でも活用できると思います。

配管系の伸縮の検討方法

検討の主旨としては、配管固定部に生じる最大曲げ応力σが配管固定部の許容曲げ応力以下になっているかを確認します。

伸縮性を持たせるために下図のような伸縮性を持たせた配管形状を考えます。

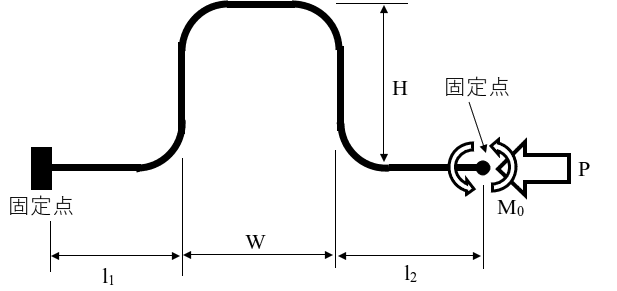
以下記号の定義です。

Ｒ：配管エルボ部の曲げ半径

ｒ：配管外半径

ｔ：配管の厚み

λ：配管の形状係

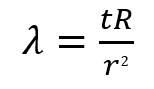
Mo：配管曲げ部に生じるモーメント

⊿：配管（l1+W+L2）の長さにおける熱膨張長さ

Ｉ：配管の断面2次モーメント

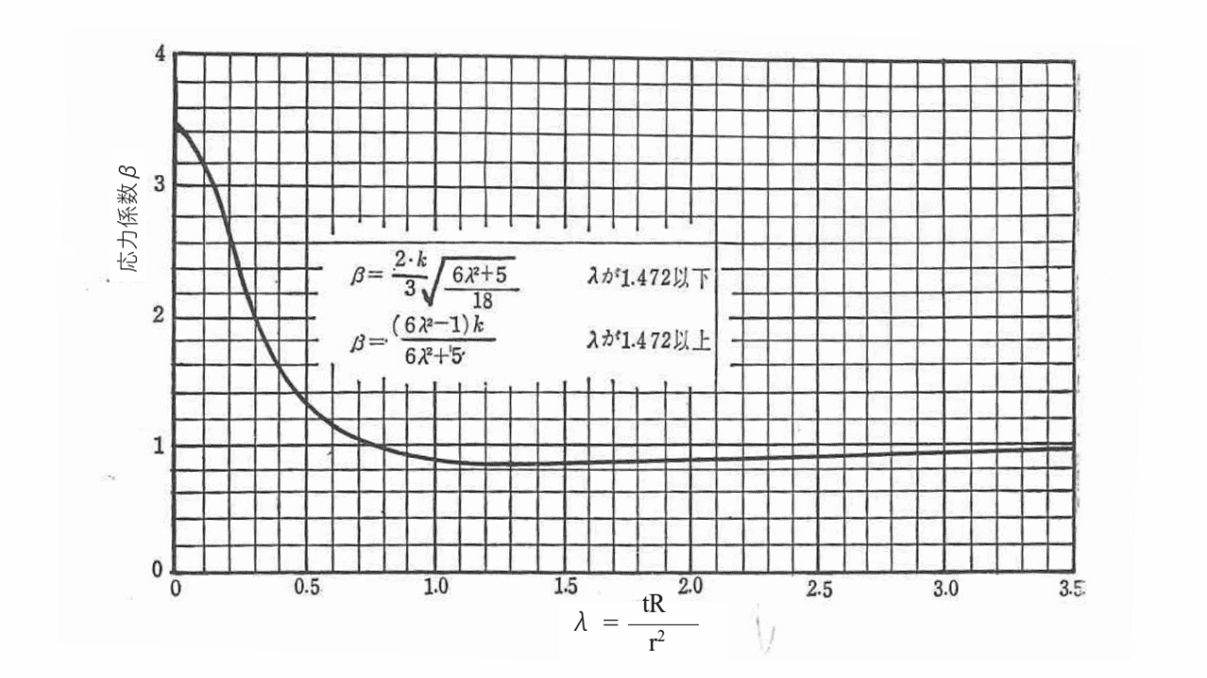
β：応力係数（配管がへん平する為の補正係数）

下のグラフからβを読み取るか、以下の式から計算しても良いです。

λの値が1.472以下の場合は、

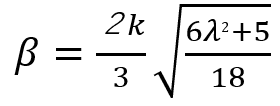
λの値が1.472以下の場合は、

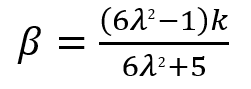
※k（剛性係数）の値は

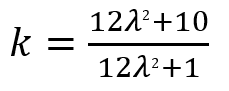
で求める。

グラフ.βとλの関係

引用:小河内 美男著、「応用機械設計 配管工学」 発行:工学図書株式会社

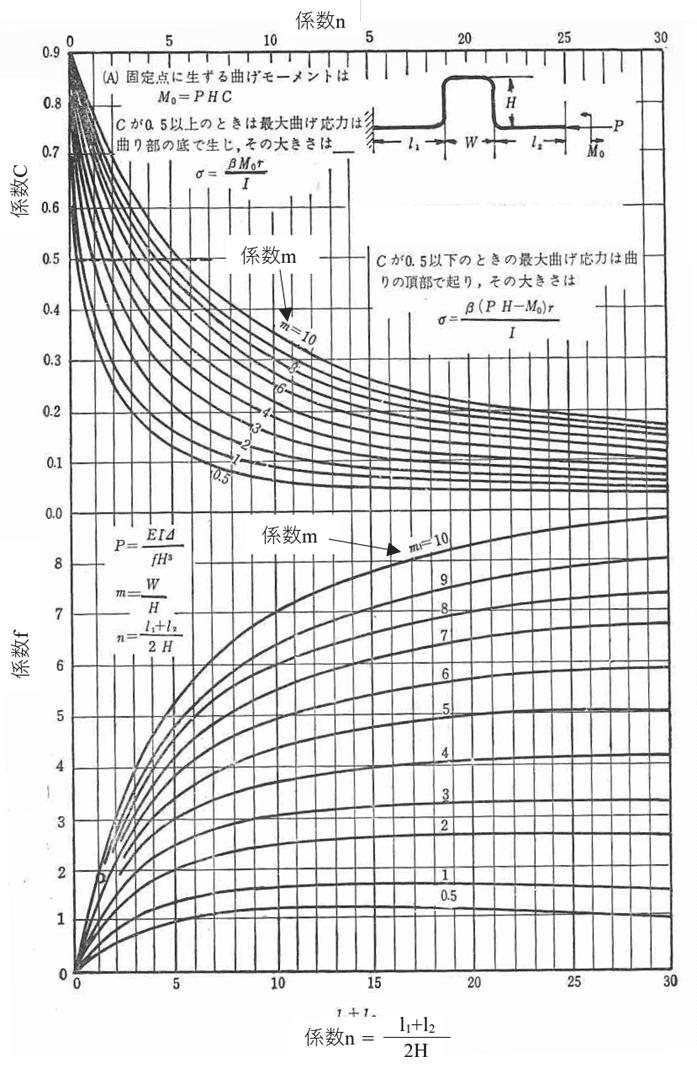
σ：配管に生じる最大曲げモーメント

Ｃ：係数（下グラフより読み取る）

ｆ：係数（下グラフより読み取る）

ｍ：曲がり部の高さと幅の比

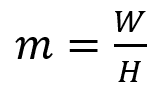
ｎ：曲がり部の高さと直管部の高さとの比

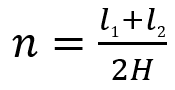
P：固定部に生じる軸方向圧縮応力

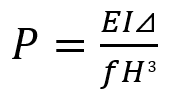
固定部で発生するモーメントM0の式は

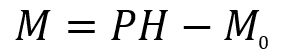
で求めることが出来ます。

Cの値によって配管に与える曲げ応力の式が変わります。

Cの値が0.5以上の場合

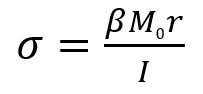
Cの値が0.5以下の場合

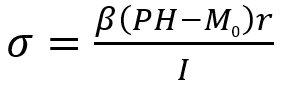
このσの値が配管固定部の許容曲げ応力以下であることを確認すれば良いです。

ちなみに配管曲げ部に生じる曲げ応力Mは、

で求められますので、配管の許容曲げ応力を超えていないかも同時に確認しておくと良いでしょう。

グラフ.係数n,f,Cの関係

引用:小河内 美男著、「応用機械設計 配管工学」 発行:工学図書株式会社

• 熱設計を学ぶ