ヌセルト数という無次元数をご存じでしょうか？

このヌセルト数という値は、対流する流体の熱伝導と熱伝達率の比を表した無次元数です。

流体力学で無次元数と聞くとおそらくまず頭に思い浮かべるのは、レイノルズ数Reなのかもしれません。流体の状態を表す際にレイノルズ数は非常に便利だからです。

しかし、熱が流体中をどのように伝わるかを考える際は、ヌセルト数の値で熱の伝わりやすさが決まります。このヌセルト数が熱流体力学の計算を行う上で非常に重要な値となるのです。

一般的にヌセルト数を記号で表す際は、「Nu」が用いられます。そのヌセルト数Ｎuは、熱伝達率α[W/m²K]、代表長さＬ[m]、熱伝導率をk[W/mK]を使って以下の式で表されます。

一方で熱伝達の式は、熱伝達率をα[W/m²K]とした際、熱伝達で伝わる熱量は、以下の式で決まります。

単位面積当たりの熱伝達の熱量＝α×流体の温度差

この式が非常にシンプルなので、簡単に伝達熱量を計算できると考えてしまいそうです。しかし、熱伝達率の値は、温度境界の状態と流れの状態によって決まる値であり、物質固有の値を持っていません。

水なら1W/m²Kであるとか、油なら10W/m²Kになるなどの決まった値を示すわけではないのです。流れがよどんでいるのか、強制的に対流しているかの様子によって熱伝達率の値が変動することになります。

熱伝達の計算では、この熱伝達率を推測することが最も重要となります。

ではこの熱伝達率を求めるにはどうしたらいいでしょうか？

上で述べたヌセルト数の計算式①を見てください。熱伝達率αが計算式に含まれています。

その為、熱伝達率を計算で求める場合、ヌセルト数を計算式①以外の方法で算出し、熱伝達率を求めるのです。

ヌセルト数を算出するために、他にも無次元数が登場しますので少し紹介します。

温度の境界がわかるプラントル数とは？

熱伝達率は、ヌセルト数から算出することができるのですが、このヌセルト数を求めるためには「プラントル数」という無次元数を理解する必要があります。

プラントル数の式は、動粘性係数ν[m²/s]と熱拡散率κ[m²/s]の比の値であり、以下の式で表されます。

※熱拡散率とは、流体内に温度がどのように広がっていくかを表す値で、熱伝導率k[W/mK]と密度ρ[kg/m³]、比熱Ｃ[J/kgK]で計算します。流れの状態によらず、物質固有の値であることがプラントル数の特徴です。例えば、20℃の水のプラントル数は約7、空気のプラントル数は約0.7となります。

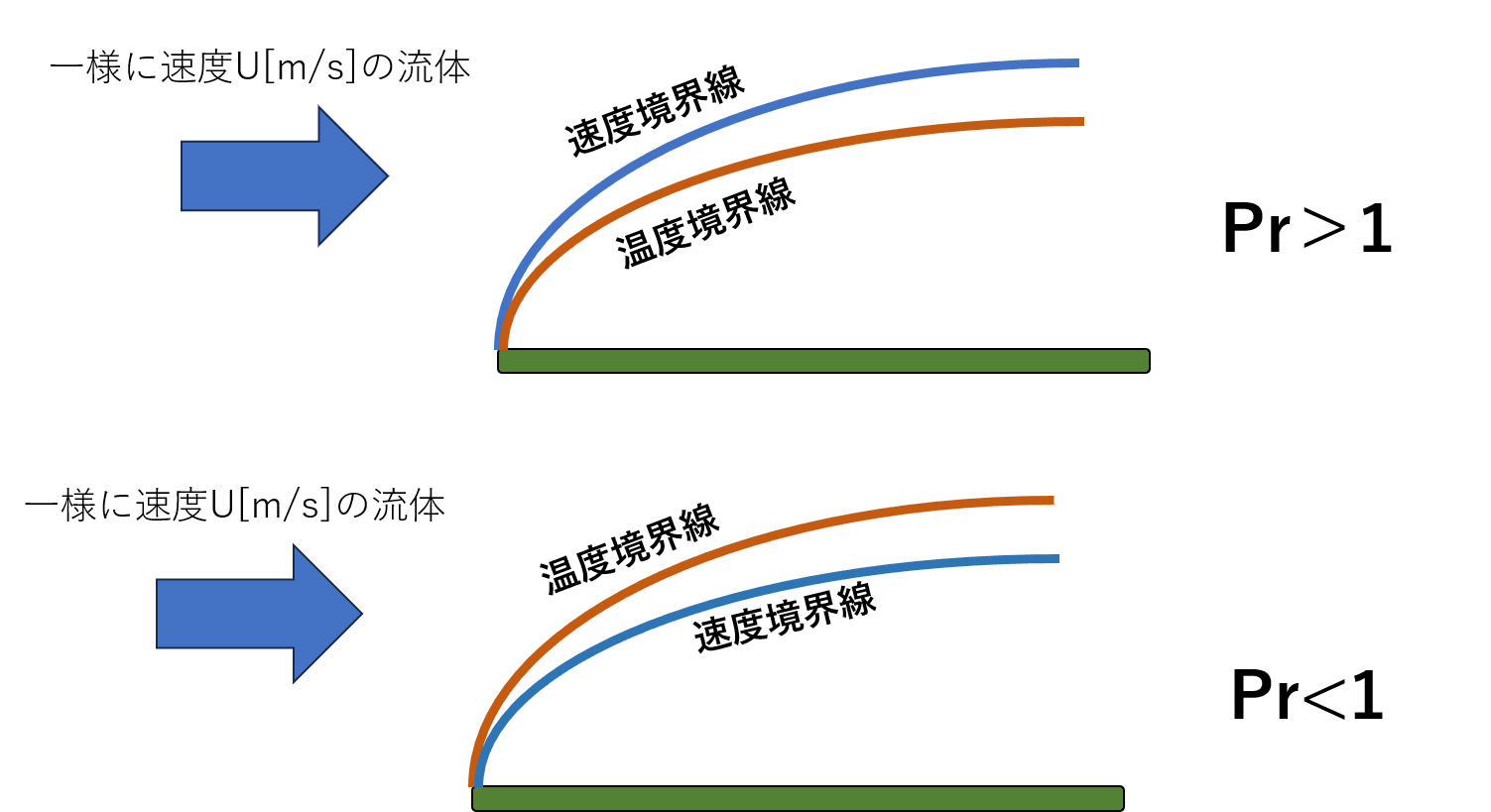
このプラントル数は、温度がどのように拡散するかを表している「温度境界層」と流速がどのように分布しているかを表す「速度境界層」の２つの層の厚みの関係を表しています。

例えば、プラントル数Pr＝１の時は、この両者の層の厚みが等しくなることを意味します。

層の厚みと聞くと少しイメージしやすくなりますね。

平面上を層流が流れる場合は、温度境界層と速度境界層との比は、以下の様に近似されるので覚えておくと便利です。

ここで、温度境界層と速度境界層について簡単に説明します。

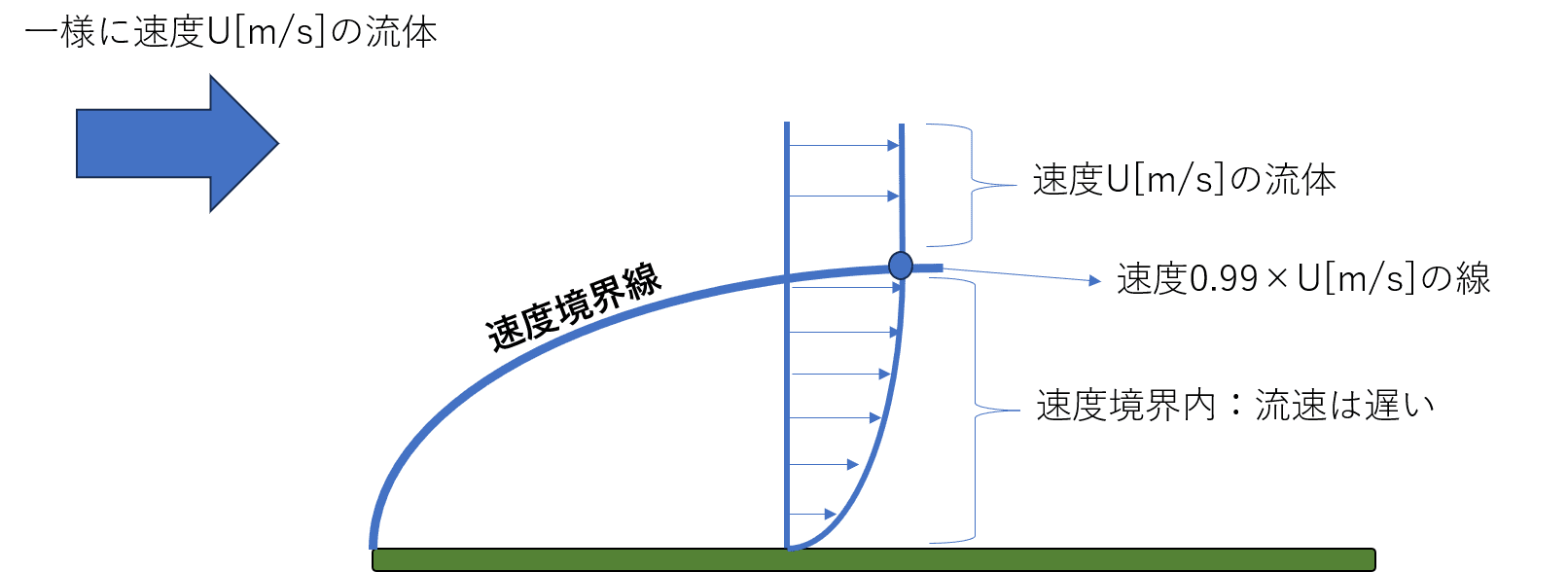
流体がある物体に沿って流れる際に、その物体表面には、速度境界と温度境界が発生します。それぞれの境界は、以下のように定められており、壁面からの距離が層の厚みということになります。

①速度境界層・・・流速が主流の流速U[m/s]の99%となる部分を境界とする。

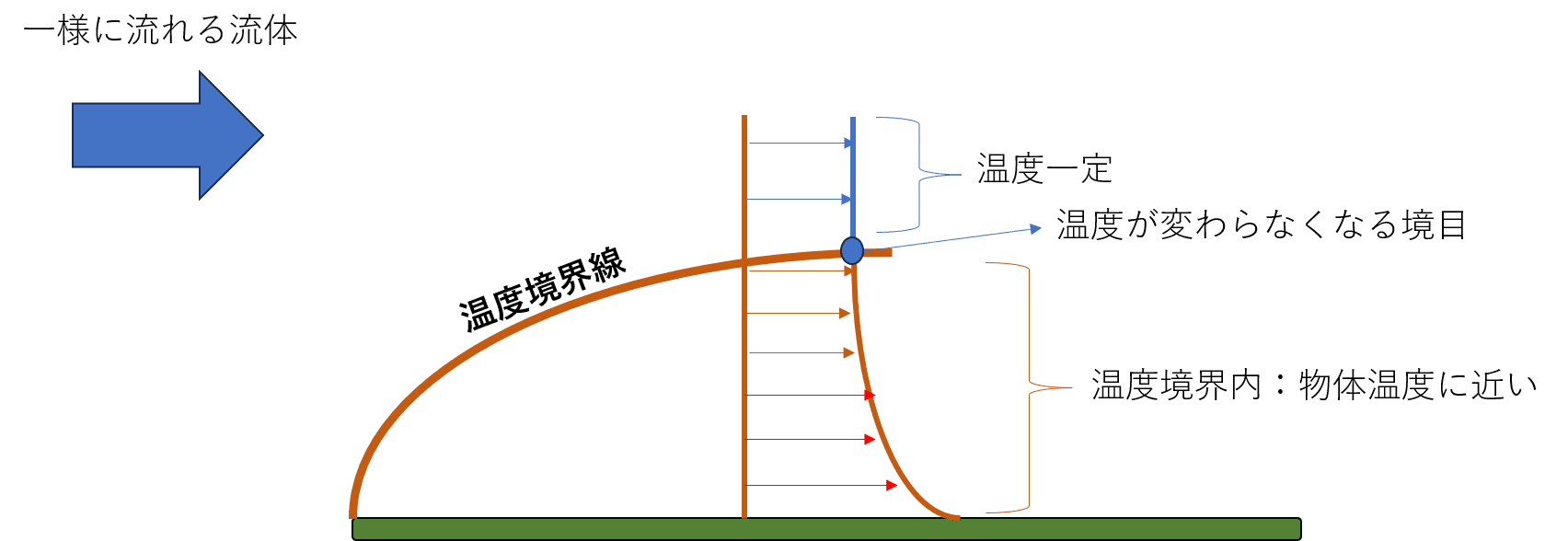
②温度境界層・・・主流の温度一定となる部分を境界とする。

プラントル数を用いてヌセルト数を求める

ヌセルト数を求める式は、様々な理論がありますが、以下のルールを知っておくと装置の設計では役に立つと思います。

ルール①：強制対流で熱伝達している流体のヌセルト数は、プラントル数の２つ用いて計算する。

例：コルバーンの式：

ルール②：自然対流で熱伝達している流体のヌセルト数は、グラスホフ数Grとプラントル数Prの２つの値を用いて計算する。

例：平面上の層流自然対流での式：

特に、ルール①の式は、実験値からヌセルト数を推測される場合は、以下の様な一般式として機器設計で用いられることがあります。

※それぞれのＡ，Ｂ，Ｃには実験値から推測された値を入れる。

まとめ

熱伝達の計算をする際には、「熱伝達率」を求める必要があります。熱伝達率は、物質固有の値を持たない為、ヌセルト数から算出することが一般的です。

しかし、そのヌセルト数は、プラントル数やレイノルズ数などの複数の無次元数の値から算出することになるため、少し面倒に感じるかもしれませんね。

• 熱設計を学ぶ