設計者の方が振動のデータを扱うようになると、「デシベル」を目にすることが多くなります。

しかし、初心者の方はデシベルの意味やその特性を理解できていない方が多いため、振動データを四則演算で処理する際に間違っているのをよく目にします。

本コラムでは、デシベルの意味や振動のデータを扱う際の具体的な計算方法を紹介します。

振動のデータの計算に自信のない方や迷っている方は、是非本コラムを参考にしてみて下さい。

振動におけるデシベル（dB）とは？

デシベル（dB）の意味

振動における加速度の周波数応答データを見ると、縦軸の値がデシベル（dB）で表示されているのを目にすることがあると思います。

しかし初めてデシベルを見た技術者の方は、データの扱いに戸惑いを感じるのではないでしょうか？

これはデシベルが、普段よく目にするメートル（m）や、グラム（g）などの、「測定値そのものの物理量を表す数字」ではなく、「ある基準に対して対数演算した相対値」であるからです。

つまり、デシベルの値は基準値によって変化してしまうため、２つのデータを比較する場合には基準値をそろえる必要があります。

デシベル値の扱いに慣れていない技術者がデータの比較で迷ってしまうのは、ほとんどがこの基準値が揃っていないことが原因です。

なお、デシベル表示に対して通常のデータをそのまま表示することを「線形表示（リニア表示）」と呼びます。

また、デシベルのデシ（d）は、10^-1を表しており、キロ（k：10³）やメガ（M：10⁶）などと同じ「SI接頭語」と呼ばれる記号です。

デシベルのベル（B）は、基準となる物理量に対する物理量の比を対数で表した量を示しています。

例えば、Aが基準値A0の100倍大きい場合をベルで表すと、

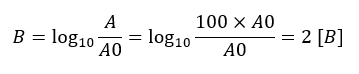
となります。

振動以外の分野でのデシベル

デシベルはあくまで基準値に対する相対比を示した値であるため、振動以外のさまざまな分野でも使用されます。

以下に工学分野において、よく使用されるデシベルを紹介します。

電気・通信系や音響系でデシベルを使用する場合に同じ分野内で別の単位を示す場合があるため、データを扱い慣れていない人が混乱する原因となっています。

その対策としてdBの後ろに記号を追加する方法（dBm:電力、dBV:電圧をそれぞれ示す）や、0dB（基準値）の数字および単位を記載する方法（dB[0dB = 10^-5 m/s²]:加速度）があります。

これらの方法は属する会社や団体の習慣によって異なる場合があるため、初心者の方はデータを扱う前に自分が属する団体の記載方法を確認しておくようにしましょう。

対数の基礎

この章ではデシベル表現に用いられている対数の定義式を記載します。高等数学の基礎ですので、理解済みの方は読み飛ばしていただいて構いません。

以下に対数の定義式を示します。

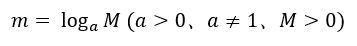
ここで、mを「対数」、aを「底」、Mを「真数」と呼びます。

対数は「底：a及び真数：Mが0以下」では成立しません。

また、対数：mは　「底：a」　の値によって変化します。

以下によく利用される底の値と、その対数の呼称を示します。

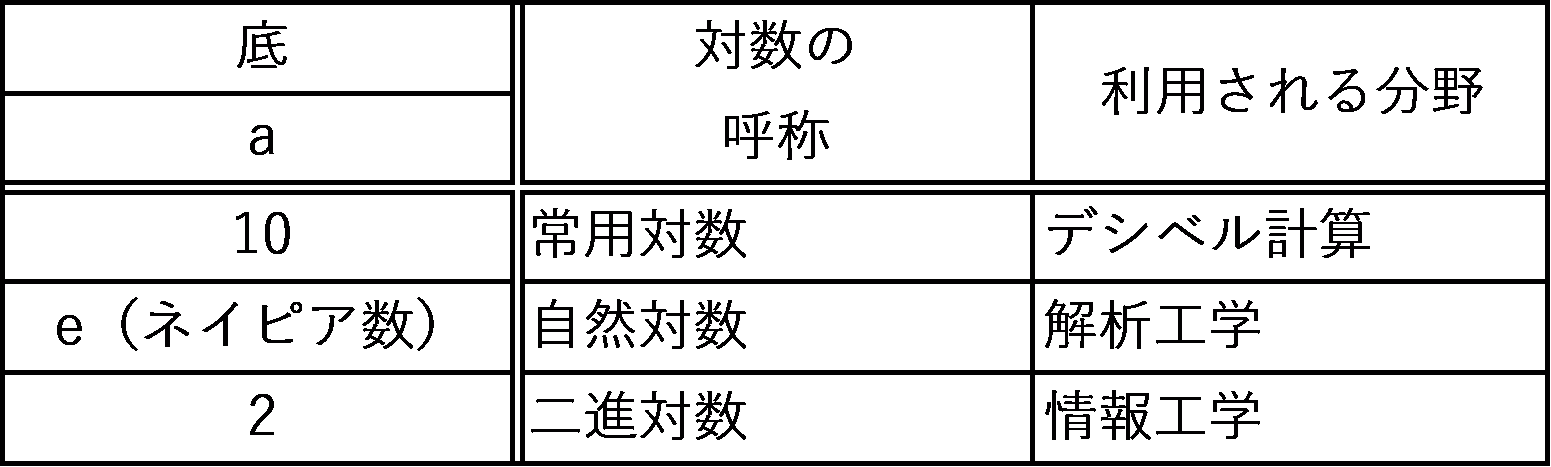
デシベル計算では底の値が10となる、「常用対数」を用います。

また、デシベル計算で良く用いられる対数の公式を以下に示します。（m、nは対数、M、Nは真数です）

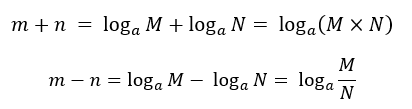
つまり、対数の足し算及び引き算は、真値では乗算及び除算となります。

これはデシベル値を計算する時も同様です。デシベル表示のデータの扱いに慣れていない方は、よく間違える点なので注意するようにしましょう。

振動におけるデシベルの定義

では次に振動におけるdB表示の定義を示します。

振動の計測量には通常加速度が用いられ、デシベル表示した値を「加速度レベル」とし、以下の式で定義されます。

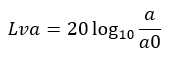
ここで、aが「振動加速度：[m/s²]」、　a0は「基準加速度： [m/s²]」です。

なお、基準加速度：a0は、JIS（日本工業規格）とISO（国際標準化機構）で値が異なっており、JISが10^-5 [m/s²]、ISOが10^-6 [m/s²]としています。

このため、同じ加速度を測定している場合でも、日本の計測機の表示とISO表示で、20dBの差があります。

JISの値が10^-5なのは、1966年に振動評価をISOで提案された基準加速度が10^-5であり、1974年にJISに基準加速度を取り入れた際にも10^-5が推奨されていたからです。

しかし、1985年からはISOでは10^-6が推奨されます。既に国内で広く一般化されてしまった10^-5を変えることが難しかったため、JISとISOで基準加速度が異なってしまいました。

国内の伝統的なメーカーでは10^-5が使われることが多いですが、海外の論文などには10^-6が使われており20dBの差があるため、デシベル表示のデータの扱いには注意が必要です。

デシベル表示のメリット

感覚値の評価に適している

振動や音響系のデータを取り扱う際にデシベルを用いる一番のメリットは、対数で表示することが人間の感覚に合っているためです。

音や明るさ、重さなどを人間が感じる際、その刺激に対する感じ方は、Weber-Fechnerの法則から受ける刺激の強さの対数に比例することが知られています。

例えば、①10 [m/s²]から100 [m/s²]に振動の加速度を変化させた場合と、

②100 [m/s²]から190 [m/s²]に変化させた場合、

③100 [m/s²]から1000 [m/s²]に変化させた場合をそれぞれ考えます。

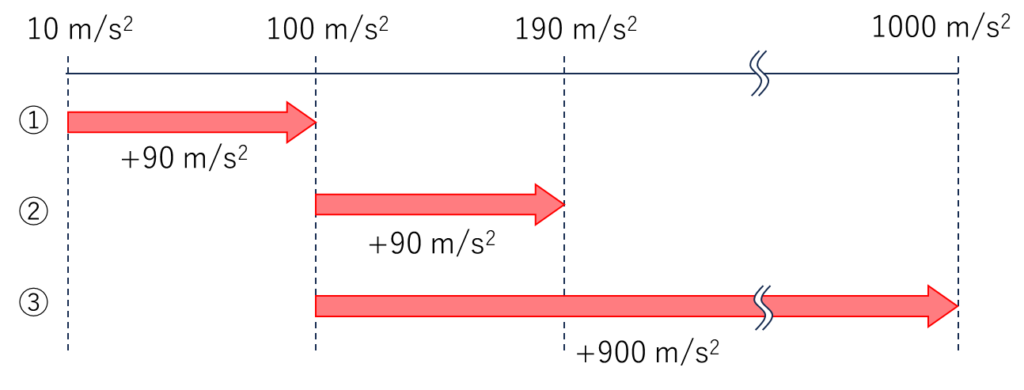
①と②では、加速度はどちらも90 [m/s²] ずつ増えているため、絶対量で比較すると増分は同じです。

しかし、①と②を触って比較すると、振動（加速度）が増えた感覚が異なります。

一方で①と③では、加速度の絶対量の増分は①90[m/s²]と③900[m/s²]で異なりますが、常用対数で比較するとどちらも増分は2となり同じです。

また、触ってみると振動（加速度）が増えた感覚は同じように感じます。

つまり、振動や音響系のように人の感覚に影響する物理量は対数に比例するため、デシベル値の差をそのまま感覚の差に置き換えられるため、線形の値よりも評価がしやすいというメリットがあります。

広い範囲の数字を表示しやすい

デシベル表示のメリットの一つに、広い範囲の数字を表示しやすいことがあります。

以下に示すような2自由度系のモデルを加振した時の加速度を、線形・デシベル表示する場合のグラフをそれぞれ示します。

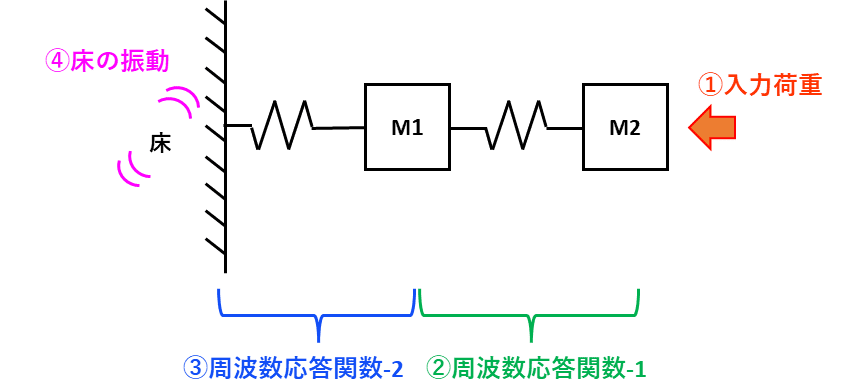
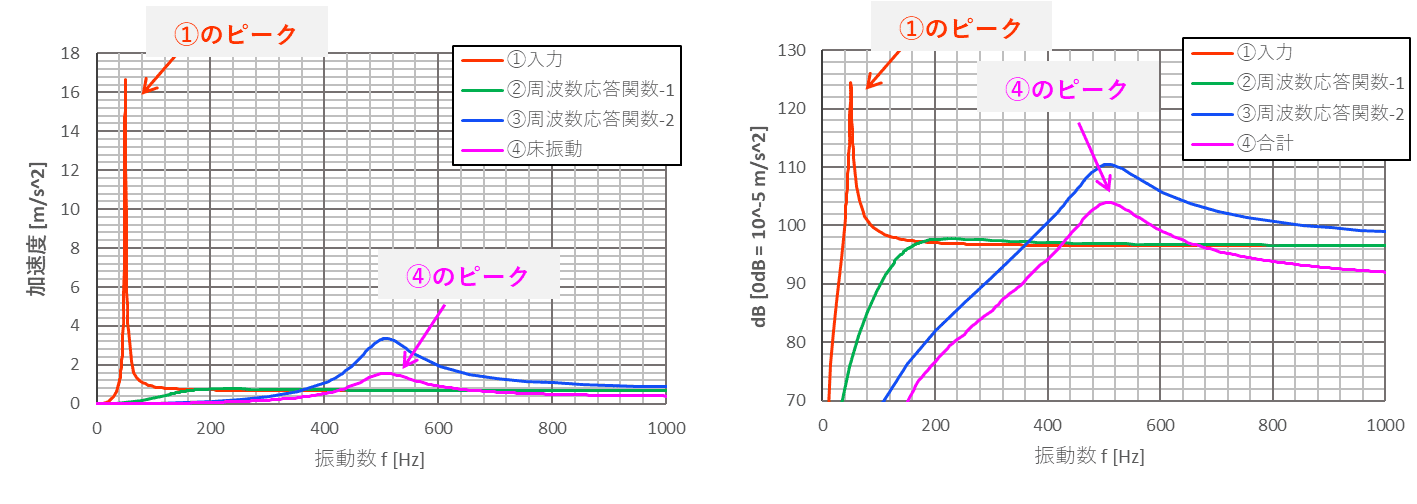
線形表示を左図、デシベル表示を右図に示しています。

図から分かるように、①の入力荷重のピークは50Hz付近にあり、加速度としては一番大きな値となります。

しかし、振動が伝わる大きさを示す②、③が、50Hz付近では非常に小さいため、最終的に床に伝わる振動である④のピークは500Hz付近となります。

これらを一つのグラフにまとめて示そうとすると、左図である線形表示では一番大きな値である①のピーク値に合わせて縦軸の大きさが変わってしまうため、肝心の床に伝わる振動量の値が読みづらくなってしまっています。

一方で右図のようにデシベル表示にすると、全てのデータを比較しやすくなることが分かります。

このように、共振周波数とそれ以外の加速度の値が大きく異なるような振動系のデータを比較する場合にはデシベル表示が有効です。

デシベル値の計算_実践編

この章では、具体的な値を用いてデシベルの値を計算してみましょう。

デシベルの定義は前出した通り、以下の式となります。

• 機械力学