「慣性モーメント（イナーシャ）」は、物体の回転のしやすさを示す重要な物理量です。モーターの設計計算をはじめ、さまざまな工学分野で活用されています。

身近な例として、フィギュアスケート選手がスピンするとき、腕や脚を体に引き寄せると回転が速くなる現象があります。これは、慣性モーメントとトルクの関係を直感的に理解するのに最適です。

本記事では、慣性モーメントの基本から具体的な計算方法までを分かりやすく解説します！

慣性モーメント（イナーシャ）とトルクの関係

直線運動と回転運動の関係

慣性モーメント（イナーシャ）とトルクの関係を理解する前に、まずは直線運動における「力」と「加速度」の関係を確認しましょう。

直線運動では、物体の質量、加速度、そしてその関係は次の式で表されます。

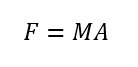
この式は、「質量が大きいほど、同じ加速度を得るためには大きな力が必要になる」ということを示しています。この関係を回転運動に置き換えたものが、慣性モーメントとトルクの関係です。式で表すと次式になります。

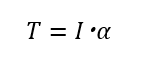
Tがトルク、Iが慣性モーメント、αが角加速度です。

力(Ｆ) → トルク(T)
質量(M) → 慣性モーメント(I)
加速度(A) → 角加速度(α)

と置き換えた式になっています。

慣性モーメントとは

質量は直線運動において「動きやすさ」を決める要素ですが、回転運動では「慣性モーメント」がその役割を担います。

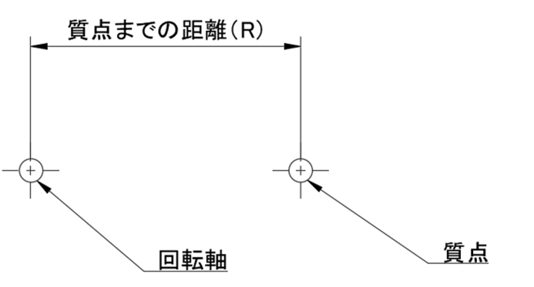
例えば、回転軸から質点までの距離がRだった場合の、質点の慣性モーメントは、質点の回転軸からの距離の二乗と、質量の積として表されます。そして、質点がたくさん集まった物質の慣性モーメントは質点の物質の和として次式で表せます。

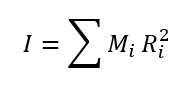
実際の物体は質点のような点ではなく、連続的なものなので、厳密には積分を用いた式で表しますが、基本的な考え方は同じです。Miを限りなく小さくしてdmに変更すると次式が得られます。

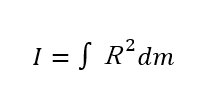
トルクと慣性モーメントの関係

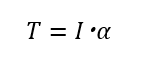
この式から、物体の回転を速くする（角加速度を大きくする）ためには、慣性モーメント(I)が大きいほどより大きなトルク(T)が必要であることが分かります。また、トルクと慣性モーメントの関係をより直感的に理解するために、慣性モーメントを質量と回転半径を使って表すと次式になります。

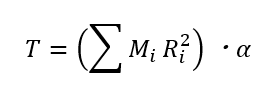
この式から、以下の場合に大きなトルク(T)が必要になることが分かります。

• 質量(M)が大きい
• 質点の距離(R)が長い
• 角加速度(α)が大きい

特に距離 は2乗に比例するため、回転軸から遠くにある質量ほど影響が大きくなります。

慣性モーメントの身近な例

慣性モーメントとトルクの関係は、私たちの身近なところでも見ることができます。

フィギュアスケートのスピン

スケーターが腕を体に引き寄せるとスピンの速度が上がります。これは、腕を広げた状態では慣性モーメントが大きく、腕を縮めることで慣性モーメントが小さくなり、角加速度が増すためです。

車の発進と加速

車を急発進させるとき、アクセルを強く踏むとエンジンが大きなトルクを発生させ、角加速度が増します。逆に、ゆっくりとした加速ではトルクが小さく、角加速度も緩やかになります。

モーターの設計

モーターを動作させる際、慣性モーメントが大きいと加速や減速に必要なトルクが増えます。設計の際には、慣性モーメントを考慮して適切なトルクを計算することが重要です。

慣性モーメント（イナーシャ）の求め方

慣性モーメントは、本来は積分を用いて求める必要があります。しかし、特定の形状に対してはあらかじめ求められた公式が存在するため、通常の計算ではこれらの公式を利用します。以下に、代表的な形状ごとの慣性モーメントの公式を紹介します。

1) 棒の端を回転軸にした場合

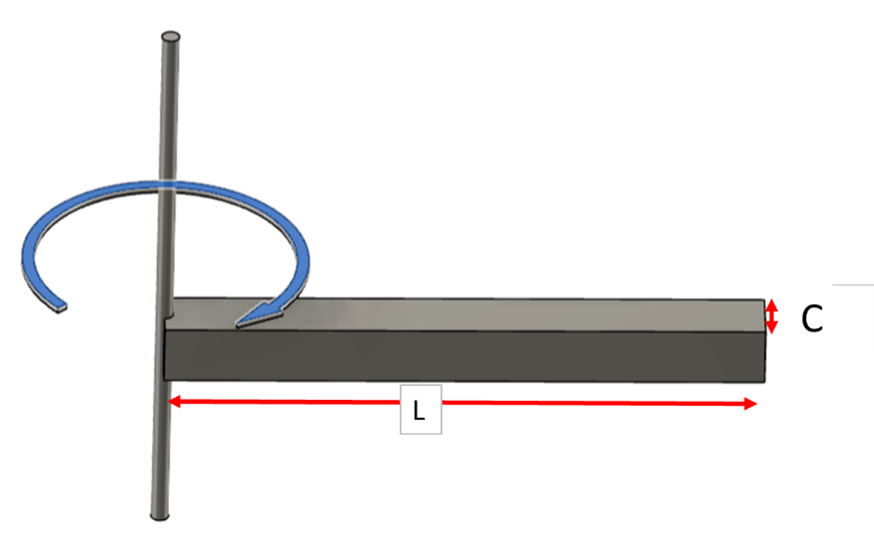
質量(M)、長さ(L)、幅(C) の一様な棒の慣性モーメント

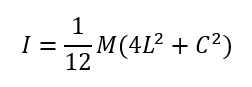
2)円盤の中央を回転軸にした円盤の公式

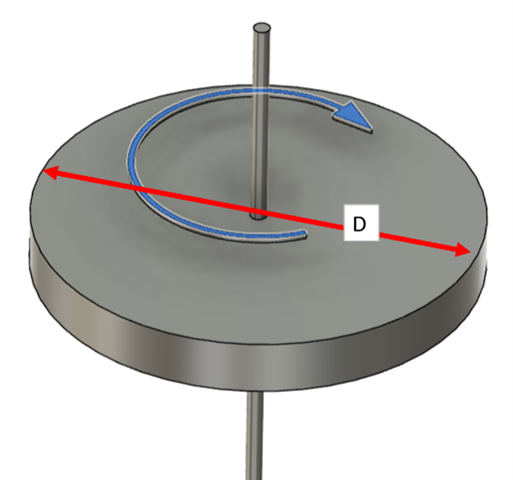
質量(M)直径(D)の一様な円盤で、円盤の中央を回転軸としたときの慣性モーメント

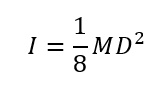
3)球の中心を回転軸にした球の公式

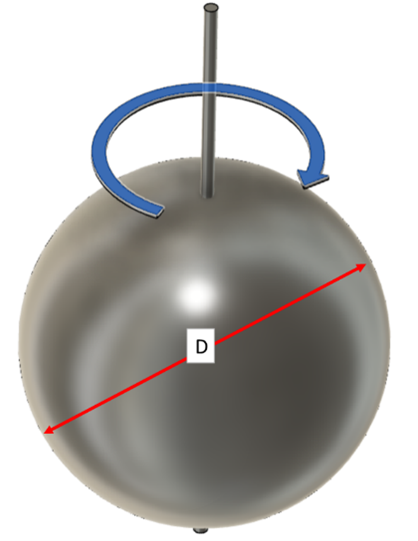
質量 (M)で直径(D)の一様な球の慣性モーメント

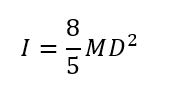
変速機がある場合の公式

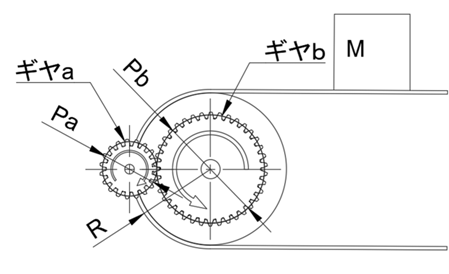
ピッチ円径を(Pa)、(Pb)、コンベアに乗った物質の質量(M) とした時のギヤa軸周りの等価慣性モーメント(I)

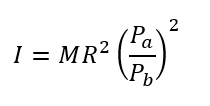
慣性モーメント（イナーシャ）の計算例

具体的な計算例として、ベルトコンベアとギヤ列の慣性モーメントを解説します。今回の例では、計算をシンプルにするために、ローラーやベルト、歯車の質量は考慮せず、基本的な概念を理解しやすい形で説明します。

1)ベルトコンベアの慣性モーメント（イナーシャ）

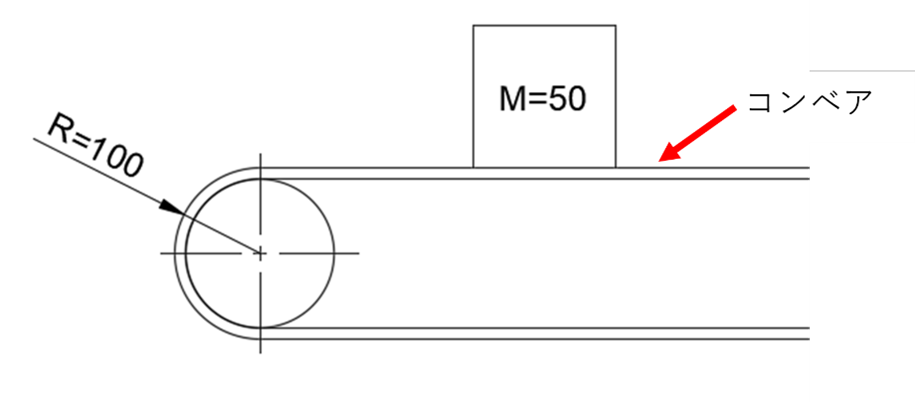
半径R=100ｍｍのローラーについたベルトコンベアの上に、重さM=50㎏の物体が載っていて摩擦抵抗はμ＝0.3とします。この時のローラーの駆動トルク（Tb）は下式で計算できます。

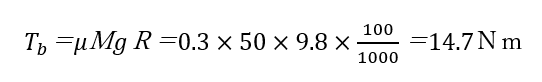
この式は T=FR がもとになっており、今回の場合、Fが摩擦力なので、μMgになります。この式で求めた14.7Nmは、ベルトコンベアを定速で動かすときに常に必要なトルクです。

2)加速するときの慣性モーメント（イナーシャ）

しかし、ベルトコンベアを加速させるときには、もっと大きなトルクが必要です。

例えば、ベルトが停止した状態から速度V=40ｍｍ/sになるまで2秒かかったとします。その時のトルクを考えてみましょう。

トルクを計算するには慣性モーメントと角加速度が必要です。

この場合、慣性モーメント(Is)は公式から次式で計算できます。

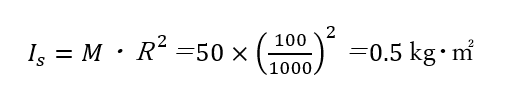
ここで、Mは物体の重さ、Rはローラーの半径です。ただし、単位をメートルにするために、1/1000をしています。

次に角加速度を計算しますが、その前に角速度を計算すると次式になります。

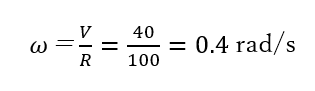
この角速度を使って角加速度(α)を計算すると次式になります。

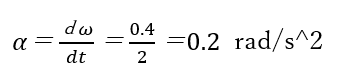
これで加速時の慣性モーメントと角加速度がわかったので、トルクが計算できます。ただし、加速時のトルクには、先ほど計算した「常に必要なトルク（Tb）」も加える必要があります。そのため、加速時のトルクは次式で計算できます。

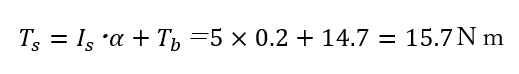
このように、ベルトコンベアを加速させるには定速で運転するより大きなトルクが必要です。この計算では2秒で定常運転（V=40ｍｍ/s）になるようしましたが、1秒で定常運転にするにはさらに大きなトルクが必要です。

3)減速機が付いたモーター軸周りの慣性モーメント（イナーシャ）

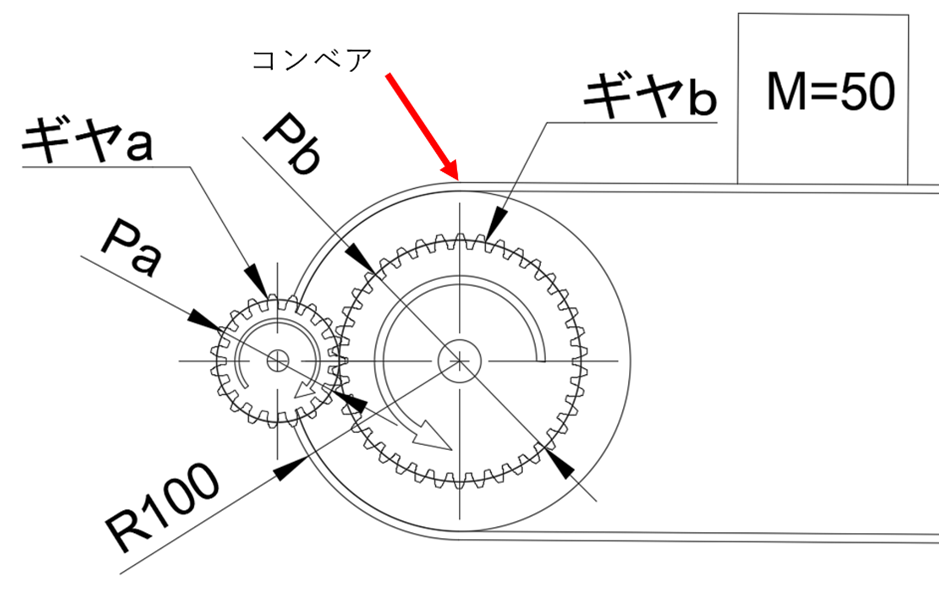
今までに計算した値は、モーターがローラを直接回転させるときに必要なトルクでしたが、ベルトコンベアを減速機付きのモーターで駆動し、モーター軸を0回転から100回転まで10秒で加速させるケースを考えます。

モーター軸にはピッチ円直径 50mm のギヤa が取り付けられ、それと噛み合うピッチ円直径 100mm のギヤb がベルトコンベアを回転させるとします。

ギヤb 軸周りの慣性モーメントは、前のステップ 2) で求めたため、モーター軸周りの慣性モーメントは公式より次式で求められます。

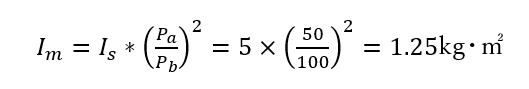
また、100回転の時の角速度(ω_m)は、次式で表せます。

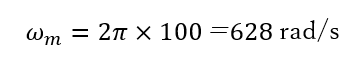
よって、0回転から100回転まで10秒で加速する場合の角加速度(α_m)は、次のようになります。

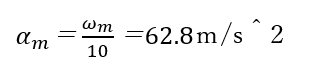
モーターの起動トルクは、モーター軸周りの慣性モーメント、角加速度、ベルトの摩擦トルクおよびギヤのピッチ円直径を考慮して次式で求められます。

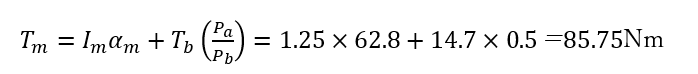
この計算結果からも、起動時には大きなトルクが必要になることが分かります。そのため、モーター選定において 起動トルク を考慮することが非常に重要です。

まとめ

慣性モーメントの計算は見落とされがちですが、短時間で所定の回転数に達する場合、大きなトルクが必要になることが分かりました。

特にモーター選定時に 定常運転時のトルク だけを考慮し、起動時のトルク を無視すると、モーターが正しく動作しないトラブルにつながる可能性があります。

このような問題を防ぐためにも、慣性モーメントを適切に考慮することが重要 です。モーター設計や機械設計を行う際には、必ず起動トルクを計算し、適切な仕様を選定しましょう。

• メカトロ
• 機械力学