新たにポンプを新設する時や配管の改造を行う際に、「配管の圧力損失を考慮することを忘れてはいけません。

配管内に流体が流れると圧力損失が生じます。その圧力損失を無視した設計をしてしまうと、流したい流量が流れないという事態だけではなく、流体のキャビテーションによる振動や配管に付けている計器類の異常につながることもあるので注意が必要です。

圧力損失は以下の式（ダルシー・ワイズバッハの式）で表せるように、配管内の流体の流速の2乗に比例する為、配管のサイズを大きくし、流速を低くすることで圧力損失を低減することができます。

h:圧力損失（m)、λ:管摩擦係数、L:配管長さ（m）、v:管内流速（m/s）、D:配管内径（m）

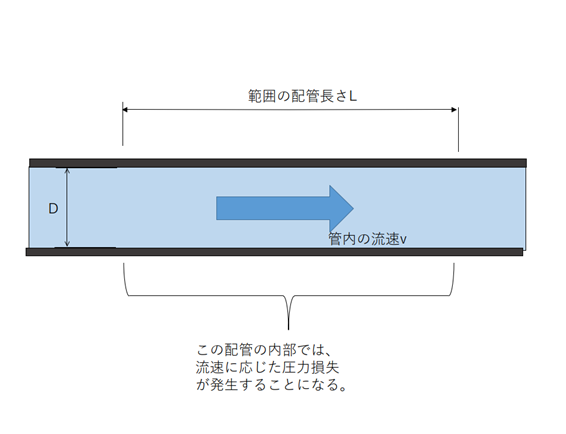
ダルシー・ワイズバッハの式の図解

しかし、流体の流速を落とす為に、配管のサイズを規格外に大きくすればよいというわけではありません。配管の圧力損失は、ある程度流速を下げると圧力損失がほどんど無いという状態（配管系統に悪影響がない状態）になるのです。そのときの理想の配管サイズを設計時に算出することが重要となります。

その為、石油化学プラント等の多くの配管が存在する工場では、プラント建設時に配管系統の圧力損失を検討し、各流体の流量に見合う配管サイズを選定しています。そうすることで、プラント建設費を抑えられ、経済的な設計が出来るようになるのです。

配管の圧力損失計算法の紹介

配管の圧力損失の算出は、上記で示したのダルシー・ワイズバッハの式をもとに考えていきます。

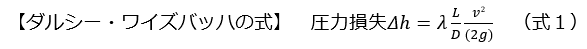
h:圧力損失（m)、λ:管摩擦係数、L:配管長さ（m）、v:管内流速（m/s）、D:配管内径（m）

計算の手順としては、まず➀レイノルズ数を算出し、流れの状態が、層流か乱流かを判断します。そして、➁その条件により管摩擦係数λを算出し、③ダルシーワイズバッハの（式１）で算出することになります。

（1）レイノルズ数の算出と層流か乱流かの判定

管摩擦係数λは、流れの状態が層流であるときと乱流であるときで計算方法が変わります。

層流か乱流かは、無次元数「レイノルズ数」によって判断出来ます。

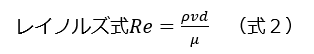
ここでρ:密度、v:管内流体速度、d:配管の内面寸法、μ:粘度

Reがその値がRe<2100では、その流体は「層流」の状態です。

Reがその値がRe>4000では、その流体は「乱流」の状態です。

2100<Re<4000の範囲内は、乱流と層流が混ざった状態となっています。

（2）層流の場合の管摩擦係数λを求める

層流の場合、管摩擦係数λの値は、レイノルズ数に反比例しており、非常にシンプルな式で算出出来ます。

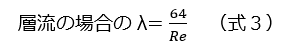
（3）乱流の場合の管摩擦係数λを求める

乱流の場合、管摩擦係数λの値を求める式は、数多くの数式が存在しますが、以下のコールブルック・ホワイトの式が実用的に使用されます。

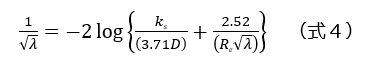
λ:管摩擦係数、ks:粒径サイズ（ｍm）、Re:レイノルズ数、D:配管内径（m）

この式では、配管内表面にある凸凹を、内面に付着した等価砂粒径サイズ（記号ks）で想定することで、実用的に管摩擦係数を算出できる式となっています。

この式３、式４をグラフにしたものが、「ムーディー線図」と呼ばれるグラフです。このグラフは工業的に頻繁に利用されています。縦軸が管摩擦係数、横軸がレイノルズ数になっています。

層流域では式３で計算され、乱流域では式４で計算します。

この式４が適用できる範囲は、以下の(式５)のλ-Re曲線とks=0となるなめらかな管に対するλ-Re曲線（式６）に囲まれた範囲となっています。

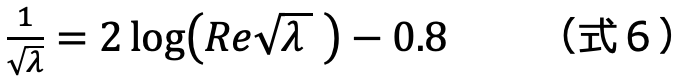
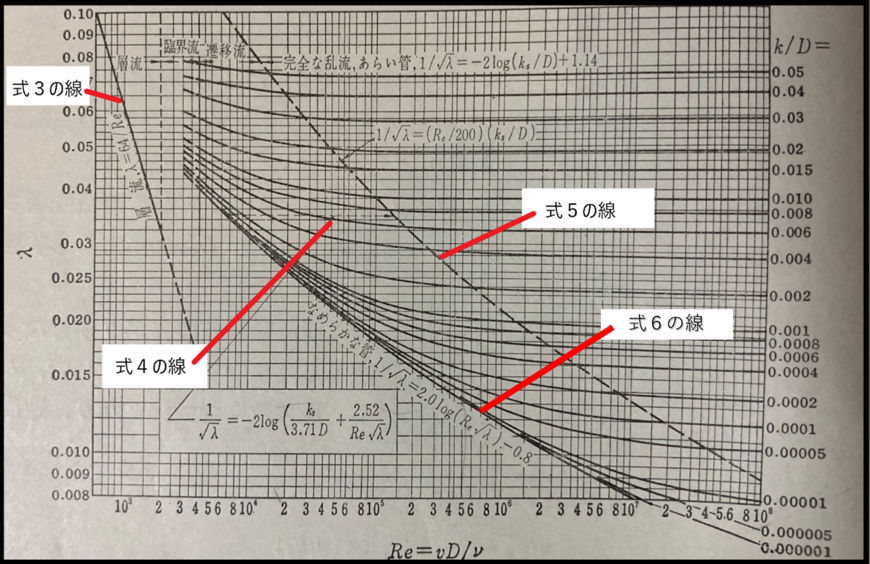
図.ムーディー線図

参照:流体固体輸送工学ハンドブック(発行:朝倉書店)

式４、式５で使用するksの値は以下の値を参考に数値を代入してみてください。

表.等価砂粒径ksの値

管の材質	壁面の状態	ks（mm）
引抜銅管,ガラス管	新しくなめらかな面	0.0013~0.0015
引抜銅管、継目無し圧延ロール管	酸洗い表面 細い管 亜鉛メッキ	0.03 0.1 0.1~0.16
溶接鋼管	新しい配管（錆なし）	0.1
使い古した鋼管	一様にさび付いた配管 ひどく水垢が付いた ひどく錆がついている 長く使ったガス配管 長く使った油系配管	0.15 2~4 2~4 0.5 1.1~2.5

設計者は配管系全体の圧力損失をイメージしなればいけない

圧力損失はストレートな配管だけでは無く、配管の形状が拡大管や分機管（ティー）や曲げ配管（エルボ）である場合も、ストレートの部分よりも多くの圧力損失を生じることになります。

又、配管だけでなく、バルブやその流体が通過する機器のすべてにおいても同様に圧力損失が発生します。その為、それら機器がどれくらいの圧力損失があるかをある程度予想して計算しなければいけません。

つまり、全圧力損失(m)=直管部の圧力損失（式１～５）＋曲げ管の圧力損失＋拡大縮小による圧力損失+合流による圧力損失＋弁や機器による圧力損失＋…と、合計した圧力損失の合計値が、その配管系全体の圧力損失となるのです。

それらの圧力損失はどう計算するか？

各種管路形状による圧力損失を計算する為に、損失係数ζ（ゼータ）を利用して以下の式6で計算します。各形状により、損失係数ζの計算方法が異なります。その算出方法についていくつか紹介いたします。

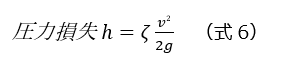
（1）急激に流路が縮小する場合

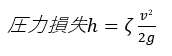
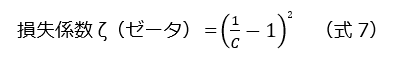
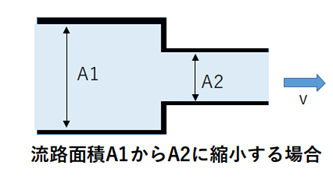
※Cは縮小係数と呼ばれ、A2/A1の値で数値が以下の表のように異なります。

表.面積比A2/A1における縮小係数の値

A2/A1	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
C	0.61	0.62	0.63	0.65	0.67	0.7	0.73	0.77	0.84

（2）縮小する間に仕切りがある場合

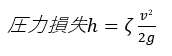
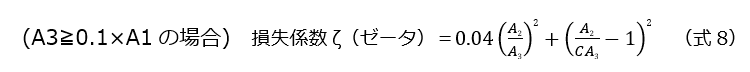
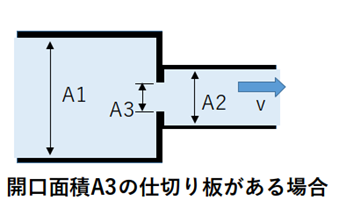
※Cは,A3/A1の値で数値が以下の表のように異なります。

表.面積比A3/A1における縮小係数の値

A3/A1	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
ζ	0.63	0.64	0.65	0.67	0.69	0.72	0.77	0.85	0.92

A3＜0.1×A1の場合は、以下の損失係数ζを使用します。

表.A3＜0.1A1の場合の損失係数ζの値

A3/A2	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
ζ	232	51	20	9.6	5.2	3.1	1.9	1.2	0.7	0.5

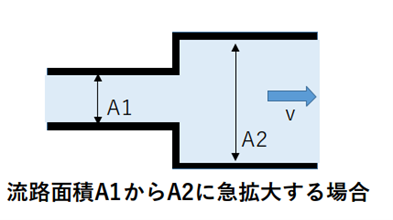
（3）急激に流路が拡大する場合

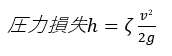
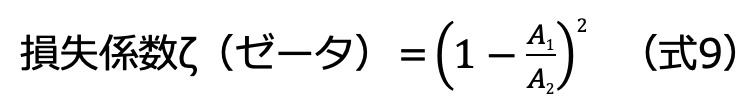
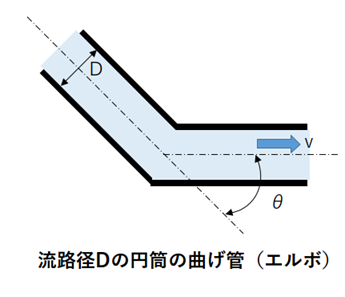
（4）曲げ管の場合

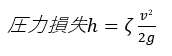
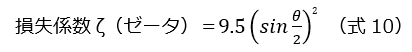
表.エルボの角度による損失係数の値

角度θ	20	40	60	80	90	100	110	120	130
ζ	0.072	0.286	0.635	1.112	1.392	1.697	2.025	2.375	2.741

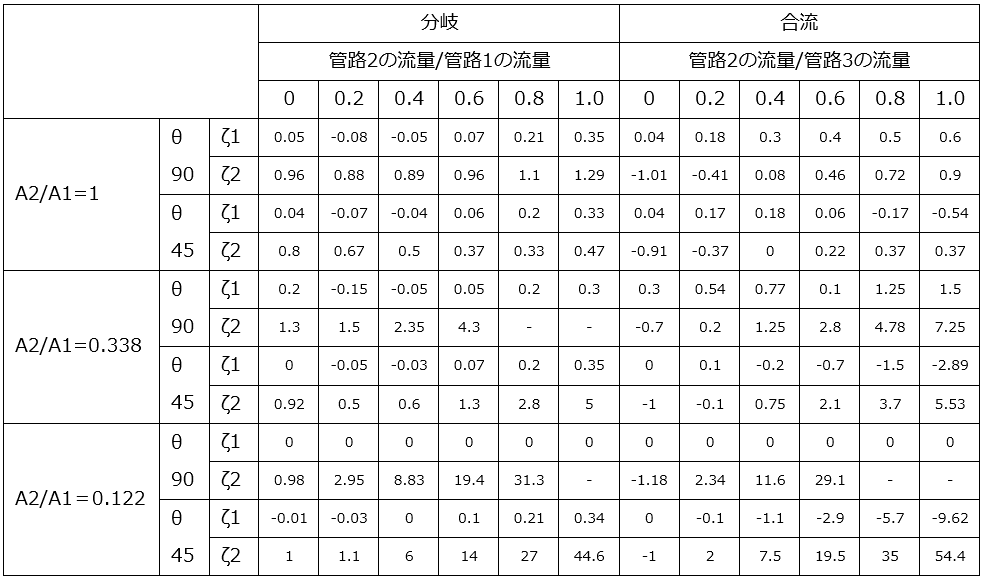
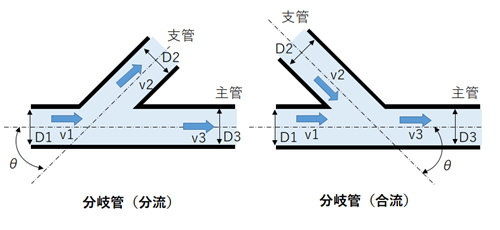
（5）分岐管の場合

分岐管は、分流と合流、主管側と支管側で考え方が異なります。以下の表に損失係数の値を記載していますので参考にしてください。

表.分岐管の圧力損失の計算法の違い（ζの値は下表の実験値を参照）

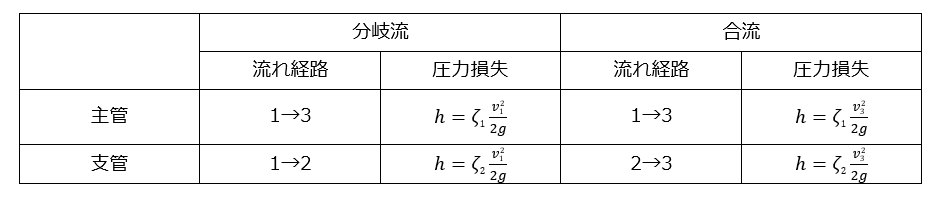
表.分岐管の損失係数ζの値（実験値）

参照:流体固体輸送工学ハンドブック(発行:朝倉書店)

（6）弁などの調節機器

弁は弁開度によって流量を変化させることができるため、圧力損失が可変であると解釈できます。

しかし実際の使用方法を想定すると、調節を行わない弁（全開で使用する弁）の場合は、以下の表により配管の長さに置き換えた場合の相当長さLeをダルシー・ワイズバッハの式（式１）で算出することになります。

※調節弁の場合は、その調節弁の圧力損失＝全圧力損失×（0.4~0.5）を想定することを推奨します。

表.相当長さLeの値

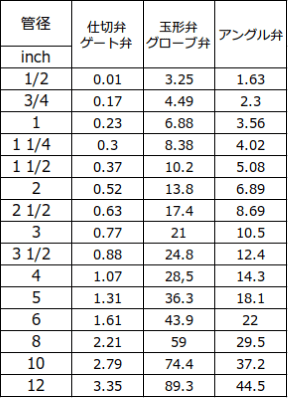
（表の値はねじ込み接続の際の値である為、フランジ接合の場合は表の値に0.9を乗じる）

現場では簡単に配管サイズを確認している

配管サイズを決めるときに、上記の圧力損失をすべて計算し求めるのが一番確実な方法ですが、少し面倒と思いませんか？

Excelで簡単に計算書を作成するのは簡単なのですが、現場や打合中の手計算では、なかなか簡単に計算は出来ません。

その為、手計算で細かく配管径を算出してもいいのですが、なるべく簡単に算出する以下の手法で算出して配管径を決定していることが多いです。

簡単な検討方法：管内の流速が以下の値になるように配管径を決める

➀液体の場合は1m/s～2m/s程度

➁ガスの場合は10m/s程度

③蒸気の場合は20m/s程度

流体の比重や粘度によって、圧力損失の値の差はありますが、配管内の流速が上記の速度であれば、経験上、圧力損失がさほど気にならない程度である為、簡単に配管径が決定できます。

• 技術計算の仕方を学ぶ
• 流体力学を学ぶ