投稿日:2025年03月19日

曲げモーメントやせん断力の計算は、機械設計や建築設計において非常に重要な役割を果たします。その計算を行う上で、特に片持ち梁は構造物や機械部品の設計でよく使われる形状です。
片持ち梁は、一端が固定され、もう一端が自由に動く梁であり、それぞれ自由端、固定端と呼ばれています。この片持ち梁に、外力がどのように作用しているかを考えて、曲げモーメントやせん断力の計算を行なうことが出来るのです。
身近な計算例としては、立て看板の柱や荷揚用のアーム、建築物の張り出し部分など、多くの場面で片持ち梁の設計が行われています。単純な片持ち梁であれば公式(下記表参照)を用いて計算できるので、公式を暗記している方もいるかもしれません。
本記事では、片持ち梁の曲げモーメントとせん断力の計算方法を中心に解説します。
特に、集中荷重、分布荷重、三角形分布荷重という3つの代表的な荷重ケースについて、それぞれの公式の求め方や曲げモーメント図とせん断力図について詳しく説明し、曲げモーメント図とせん断力図から得られる重要な情報についてまとめます。
片持ち梁のモデルと曲げモーメントとせん断力の公式
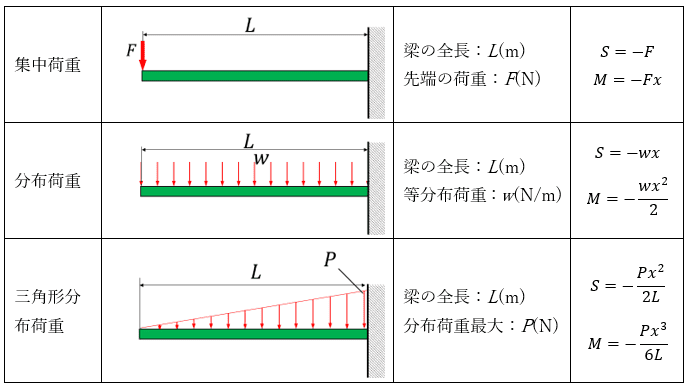
※S:せん断力、M:曲げモーメント、x :先端からの距離
このコラムを書いた人

機械系プラントエンジニア
国内化学プラントで機械設計や建設工事を10年以上経験。危険物製造設備、発電・ボイラ設備・排水処理設備、研究施設の多種多様な設計・調達・工事に携わり、その知識をコラムにて発信中。現場でも活かせる専門知識を、日本のモノづくりに活かしてもらいたい!という強い思いを持っている。
片持ち梁の曲げモーメント図とせん断力図(集中荷重)
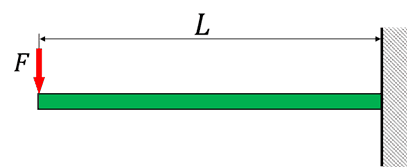
まず、曲げモーメントとせん断応力を求めるためのルールと、せん断力と曲げ応力の向きについて押さえておきましょう。
曲げモーメントとせん断応力を求めるためのルール
曲げモーメントとせん断応力を求めるためのルールは以下の2つです。
- その梁全体が外力を受けてつり合っている状態であれば、どこで切断してもその部分の合力は0となる。
- 力のモーメントの和はどの断面で切断しても0となる。
この2つのルールによって、部材をどこで切断しても、釣り合いの式が成り立つ為、切断した箇所のせん断力や曲げモーメントを求めることが出来るようになるのです。
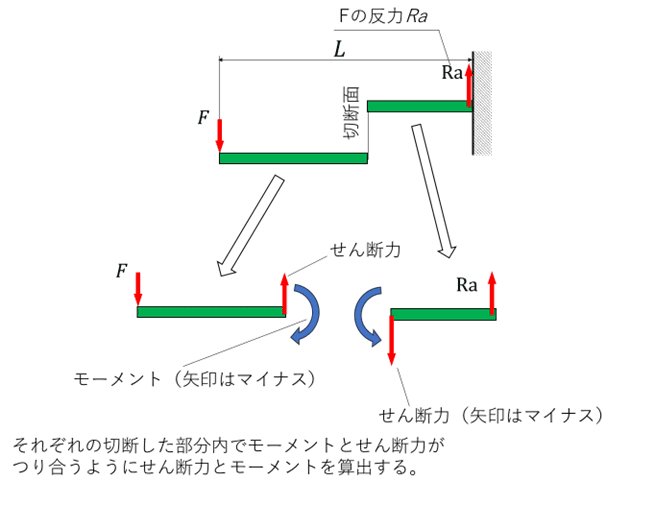
それぞれの切断した部分内でモーメントとせん断力がつり合うようにせん断力とモーメントを算出する。
せん断力と曲げ応力の向き
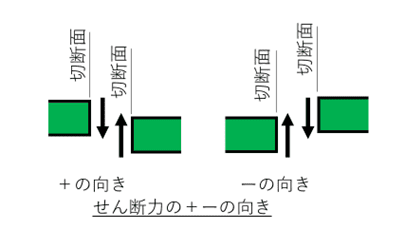
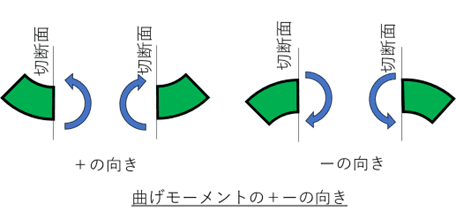
曲げモーメントやせん断力には、向き(+方向、―方向)が業界によって決まっています。本コラムで使う向きを以下の図にまとめました。業界によって正負の向きが異なることがありますが、考え方は同じです。
せん断力は、断面の左側は下向きが正で、断面の右側は、上向きが正と覚えておきましょう。又、モーメントは断面の左側は反時計回りの向きが正で、断面の右側は時計回りの向きが正となります。
1.固定部の反力を求める
曲げモーメントとせん断力を計算する前に、まずは固定部等に加わる反力を計算する必要があります。
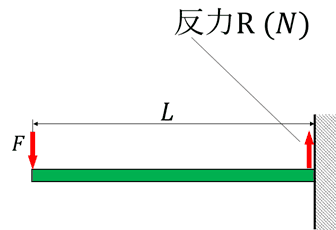
この反力Rは釣り合いより、
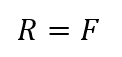
となります。
2.せん断力を求める
続いて、片持ち梁の先端に集中荷重を受けた梁に、どのように曲げモーメントとせん断力が発生しているのかを考えてみましょう。
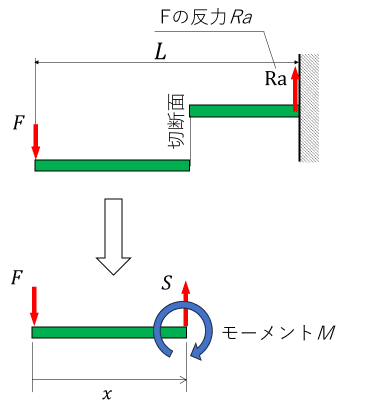
切断してモーメントとせん断力を考える(集中荷重)
(図中のモーメントMとせん断力Sの矢印の向きはマイナスの向きになっているので注意)
先端から距離xの位置で切断し釣り合いを考えると、せん断力Sは
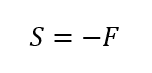
となり、固定端から自由端までは、一定のせん断力となります。断面左側でSは上向きなので負(マイナス)となります。
3.曲げモーメントを求める
先端から距離xの位置で切断しつり合うための曲げモーメントMは
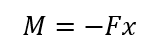
となります。曲げモーメントは、長さxの値に応じて変化していきます。
4.曲げモーメント図とせん断力図を描いてみる
曲げモーメントとせん断力を、横軸を梁の長さ、縦軸を曲げモーメント及びせん断力としてグラフに書くと、どのように梁に力が分布しているのか分かりやすく表示ができます。
機械業界では曲げモーメント図をBMD(Bending Moment Diagram)と呼び、せん断力図をSFD(Shearing Force Diagram)と呼びます。建築業界では曲げモーメント図をM図、せん断力図をQ図と呼びます。
片持ち梁(集中荷重)の曲げモーメント図とせん断力図のグラフは下の図の様になります。
5.具体的な計算をしてみよう
それでは、梁の長さが5mで先端に10Nの荷重を受けている片持ち梁の最大のせん断力と最大曲げモーメントを求めてみましょう。
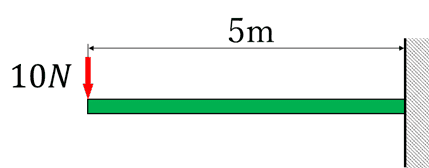
せん断力と曲げモーメントは以下の式で求められるので、最大となるx=5mを代入すると、
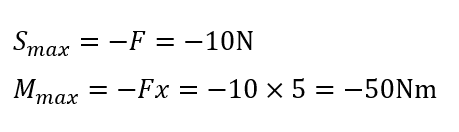
となり、それぞれ最大せん断力は-10N、最大曲げモーメントは-50Nmという値になります。
片持ち梁の曲げモーメント図とせん断力図(分布荷重)
次に片持ち梁に等分布荷重を受けているケースを考えます。
1.固定部の反力を求める
まずは固定部の反力を求めてみます。
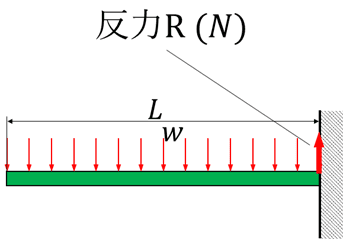
図中の下向きの力は、等分布荷重w×梁の長さLである為、反力Rは
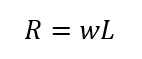
となります。
2.せん断力を求める
続いて、片持ち梁全面に等分布荷重を受けた梁に、どのように曲げモーメントとせん断力が発生しているのかを考えてみましょう。
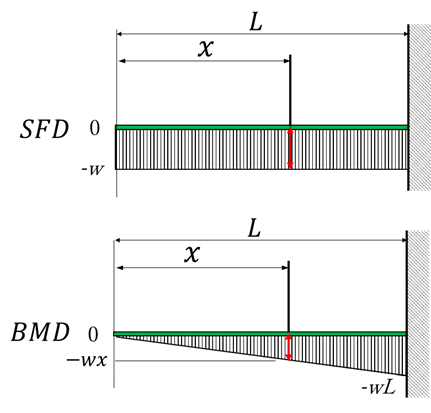
先端から距離xの位置で切断し釣り合いを考えると、せん断力Sは
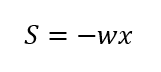
となり、先端からの距離に比例してせん断力の絶対値は大きくなります。又、切断面の左側のせん断力は上向きなので、値は負(マイナス)です。
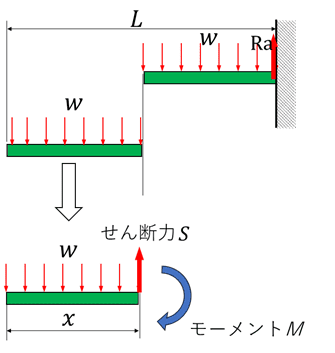
切断してモーメントとせん断力を考える(分布荷重)
(図中のモーメントMとせん断力Sの矢印の向きはマイナスの向きになっているので注意)
3.曲げモーメントを求める
先端から距離xの位置で切断しつり合うための曲げモーメントMは
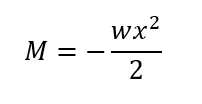
となります。曲げモーメントは、長さxの2乗の値に応じて変化していきます。又、断面の左側は時計回りの向きのモーメントである為、モーメントMは負(マイナス)です。
4.曲げモーメント図とせん断力図を描いてみる
曲げモーメント図BMDとせん断力図SFDのグラフを下に示します。
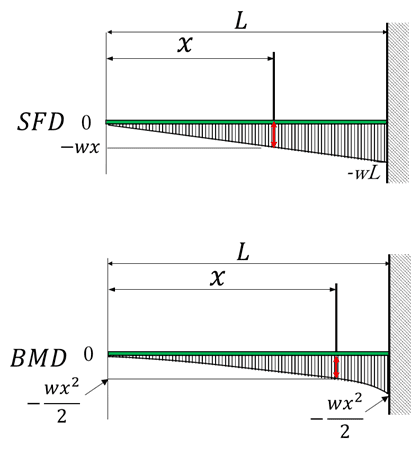
5.具体的な計算をしてみよう
それでは、梁の長さが5mで等分布荷重10N/mの荷重を受けている片持ち梁の最大のせん断力と最大曲げモーメントを求めてみましょう。
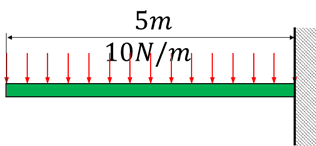
せん断力と曲げモーメントは以下の式で求められるので、最大となるx=5mを代入すると、
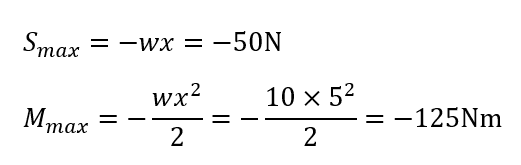
となり、それぞれ最大せん断力は-50N、最大曲げモーメントは-125Nmという値になります。
片持ち梁の曲げモーメント図とせん断力図(三角形分布荷重)
次に片持ち梁に三角形分布荷重を受けているケースを考えてみましょう。
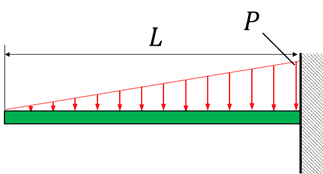
1.固定部の反力を求める
まずは固定部の反力を求めてみます。
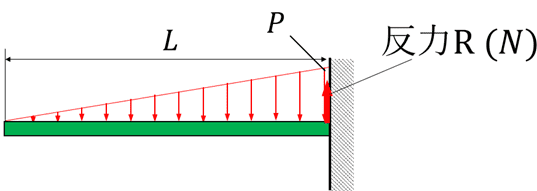
図中の下向きの力は、図中の三角形の面積である為、反力Rは
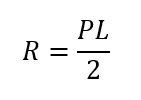
となります。
2.せん断力を求める
続いて、片持ちに三角形分布荷重を受けた梁に、どのように曲げモーメントとせん断力が発生しているのかを考えてみましょう。
先端から距離xの位置で切断し釣り合いを考えると、せん断力Sは
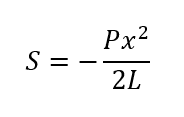
となり、先端からの距離に比例してせん断力の絶対値は大きくなります。又、切断面の左側のせん断力は上向きなので、値は負(マイナス)です。
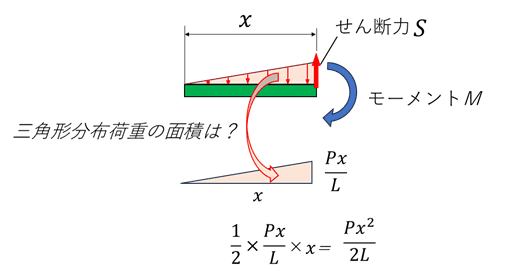
3.曲げモーメントを求める
固定端から距離xの位置で切断しつり合うための曲げモーメントMは
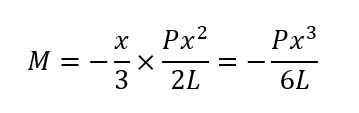
となります。曲げモーメントは、長さxの3乗の値に応じて変化していきます。又、これまでと同様に、断面の左側は時計回りの向きのモーメントである為、モーメントMは負(マイナス)です。
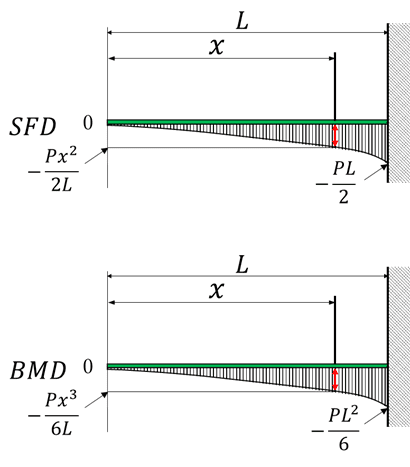
4.曲げモーメント図とせん断力図を描いてみる
曲げモーメント図BMDとせん断力図SFDのグラフを下に示します。
5.具体的な計算をしてみよう
それでは、梁の長さが5mで三角形分布荷重の最大が10Nの荷重を受けている片持ち梁の最大のせん断力と最大曲げモーメントを求めてみましょう。
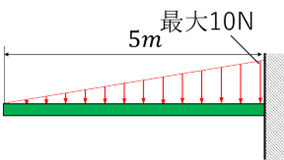
せん断力と曲げモーメントは以下の式で求められるので、最大となるx=5mを代入すると、
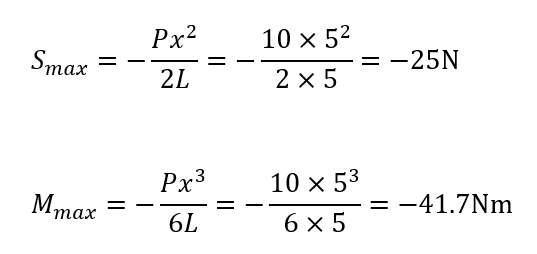
となり、それぞれ最大せん断力は-25N、最大曲げモーメントは-41.7Nmという値になります。
曲げモーメント図とせん断力図で何がわかる
曲げモーメント図やせん断力図は曲げモーメント図とせん断力図は、構造設計において以下のような重要な情報を得るために一般的に用いられています。
①最大応力が生じる位置の特定
梁のどの部分に最大曲げモーメントが発生するかをつかむことで、設計者はその箇所を重点的に補強することができます。逆に曲げモーメントが0となる点を探る際にも利用できます。
②材料の選定
最大曲げモーメントの値を基に、梁や柱に必要な材料の強度を計算できるようになります。
③変形やたわみの評価
曲げモーメント図は梁のたわみ量を評価する際にも役立ちます。特に、最大たわみが許容範囲内に収まるかを確認するために重要です。
④荷重条件に応じた設計の最適化
分布荷重や三角形分布荷重など、異なる荷重条件が発生した際に、それぞれのせん断力と曲げモーメントを加算又は減算して、応力分布を視覚的に把握することが出来ます。これにより効率的な設計が可能となるのです。
これらの情報は、設計の初期段階から施工まで、あらゆる工程で活用されます。正確な図を描き、応力分布を理解することは、信頼性の高い構造物を作り上げるための土台となるのです。
片持ち梁の曲げモーメントまとめ
片持ち梁における集中荷重、分布荷重、三角形分布荷重の各ケースにおいて、それぞれ異なる形状の曲げモーメント図とせん断力図を描くことが出来れば、構造の特性を正確に把握できるようになります。
曲げモーメントやせん断応力の公式や正負の向きは、なかなか覚えにくいかもしれません。しかし、それらの導き方や考え方を理解しておけば、問題なく計算ができるようになります。
曲げモーメント図やせん断力図をうまく活用して、機械設計における信頼性と安全性の向上を目指しましょう。