空中にボールを投げると、そのボールには空気抵抗が発生します。この空気抵抗にはどのような特徴があるのでしょうか？

空気抵抗は、物体が空気中を移動する際に、空気との摩擦や圧力のために生じる抵抗ですが、その空気抵抗の値は一定ではなく、速度に応じて変化します。空気抵抗に影響を与えるのが抗力係数という値です。

この値は、物体の形状や表面の滑らかさなどによって決まる定数で、空気抵抗を計算する際に使用されます。抗力係数が大きいほど、物体は空気抵抗によって受ける影響が大きくなります。

動く物体には、その周りにある流体が抵抗になるため、その抵抗（＝抗力）の変化を掴むことによって、航空機や粉体を扱う装置にも応用することができるようになります。

この記事ではこの抗力係数についての考え方を理解し、効力係数とレイノルズ数との関係性も説明します。

抗力係数とは何か？

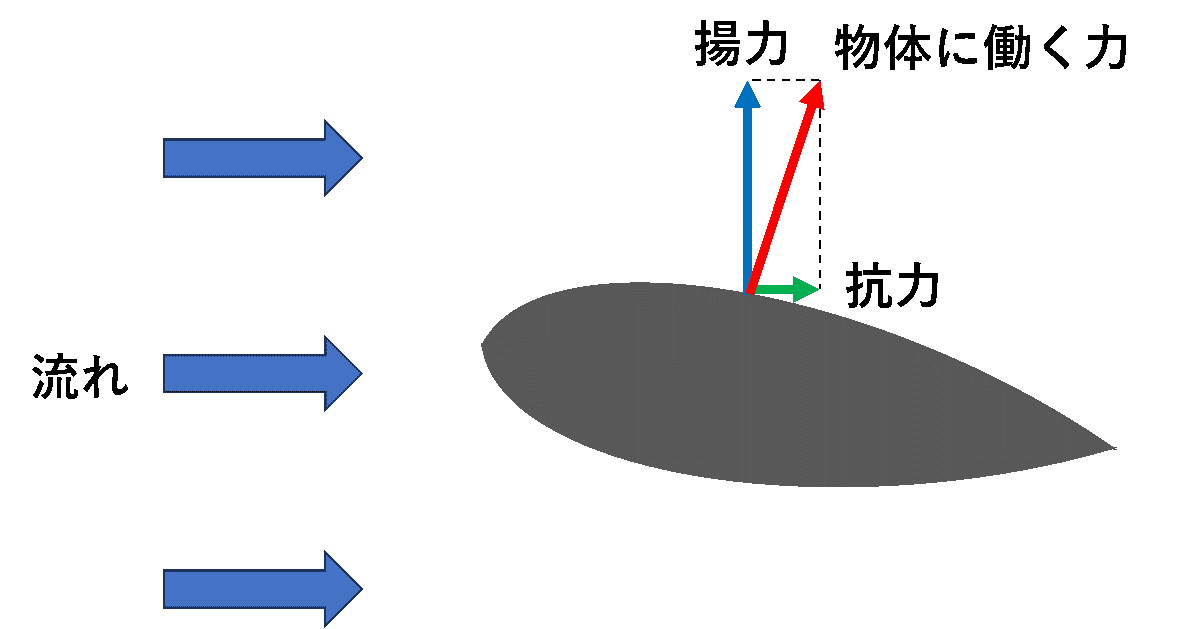
物体を一様に流れる流体の中に置くと、物体は流れから力を受けます。この力のうち、流れの方向の成分を抗力、流れに垂直な方向の成分を揚力といいます。

この抗力を主流動圧と物体の代表面積で除し無次元化した値を抗力係数とよびます。

ここで大事なことは、物体はある流れの中では、抗力と揚力の2つの力を受けるということです。もちろんその名の通り、抗力は流れ方向に押し流そうとする力で、揚力は流れと垂直に進む力です。

物体に働く力（流体から受ける力）を抗力成分と揚力成分に分けるために乗じる値が抗力係数や揚力係数と考えることができます。

主流動圧は、ベルヌーイの式から圧力を求めると、

が導かれます。これにより、抗力Dと抗力係数C _Dの関係は以下の式で表されます。

また、揚力Lにおいても、揚力係数C _Lの関係は、以下の式で表されます。

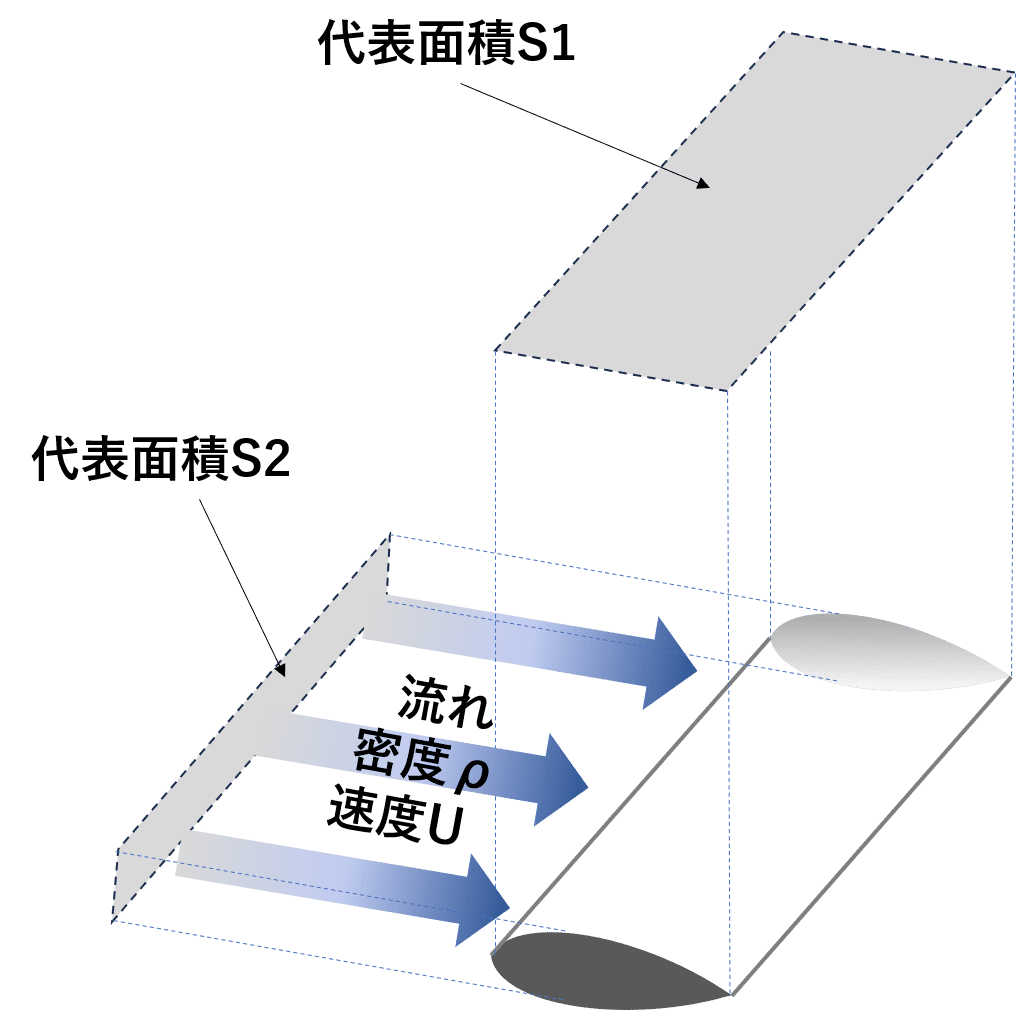
式中にある代表面積S1とS2には、抗力では流れの方向から見た投影面積S2を用いて、揚力では流れに垂直な方向から見た投影面積S１を用います。

※物体が翼の場合は、例外的に、抗力と揚力いずれの場合にも流れに垂直な方向から見た投影面積S1が用いられます。

ここまで理解した後で、以下の疑問が出てきます。

「では抗力係数はどのように算出するのか？」

答えは、この抗力係数や揚力係数は、形状や流れに対するむかえ角によって値が異なる為、実験値を用いるのが一般的な手法です。

球形状や円筒形状であれば、係数を求める式は簡単に見つかりますが、それ以外は以下の表の値を一例として用いることで計算が可能となります。

以下の表は、物体の形状における抗力係数の値を示していますが、そのまま抗力係数の値を扱う際は注意が必要です。

抵抗係数はレイノルズ数によって値が変動することを認識しておかなければいけません。そして、物体周りのレイノルズ数が、ある一定の値を超えると、抗力係数も一定になります。

表.種々の物体の抗力係数

引用元:近畿大学名誉教授 工学博士 児島忠倫HPより

抗力係数は摩擦による抗力と圧力による抗力の２つの影響によって異なる

抗力係数はなぜレイノルズ数に関係して値が変動したり一定となったりするのでしょうか？

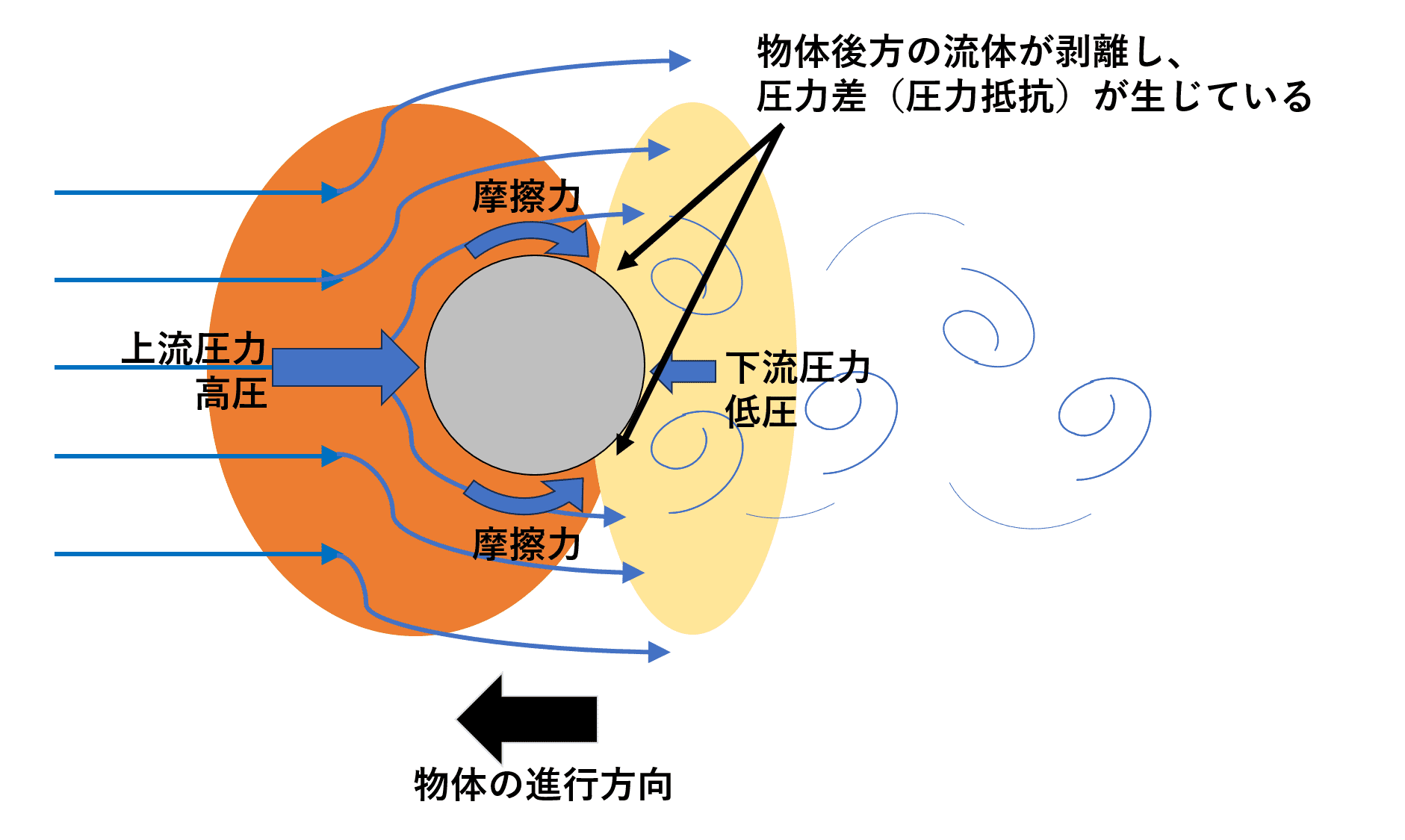
流体中に物体が移動する際、その物体には①流体から受ける摩擦と②物体進行方向の前後に生まれる圧力差によって抗力が発生するとされています。

物体の抗力となる摩擦力と圧力差の模式図

摩擦は、流体の粘性によって、物体表面で作用する摩擦に伴う抗力です。管路などの流体の流路に平行な面が大きい形状では、摩擦による抗力が支配的となります。

一方、圧力差は流れが物体後方から剥離することで、物体の前方よりも後方の圧力のほうが低くなって生じます。この剥離が起きる部分に、渦が生まれるのです。

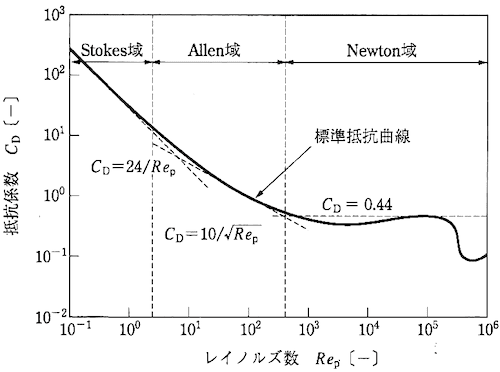
ここで、球体の物体を例として、レイノルズ数と抵抗係数の関係を考えてみます。

抵抗係数は、以下のグラフのようにレイノルズ数Reの範囲に応じて関数で表現ができます。

このグラフの中で重要なのは、レイノルズ数Reが約500を超えるとほぼ一定になっているという点です。グラフでは、抗力係数C _D＝0.44となっています。

上の表で示している抗力係数C _Dの値は、各形状におけるレイノルズ数が一定となるときの抗力係数を表しているといえます。

球体形状の物体が受ける抵抗係数（＝抗力係数）

引用元:粉体用語辞典HPより

また、このグラフではレイノルズ数が200000を超えたあたりから、抗力係数が急激に低下していることが分かります。

これは、レイノルズ数が大きくなることで、物体の表面を流れる流体が剥離する点で層流状態から乱流状態に変化し、流体剥離の位置を物体の後方にずらす効果が発生したために起きる現象です。

剥離位置が後方にずれることで、結果的に圧力差が急激に小さくなり、抗力係数も小さくなるのです。この現象が起きるときのレイノルズ数を「臨界レイノルズ数(critical Reynolds number)」と呼びます。

ゴルフボールに細かなくぼみをつけている理由は、ボール表面に人工的に乱流境界層を引き起こし、ボールの抗力係数を下げる為といわれています。

また、ボールに回転を与えるとカーブするサッカーのシュートや野球の投球も、この理論によって抗力係数が低くなる効果を応用しているのです。

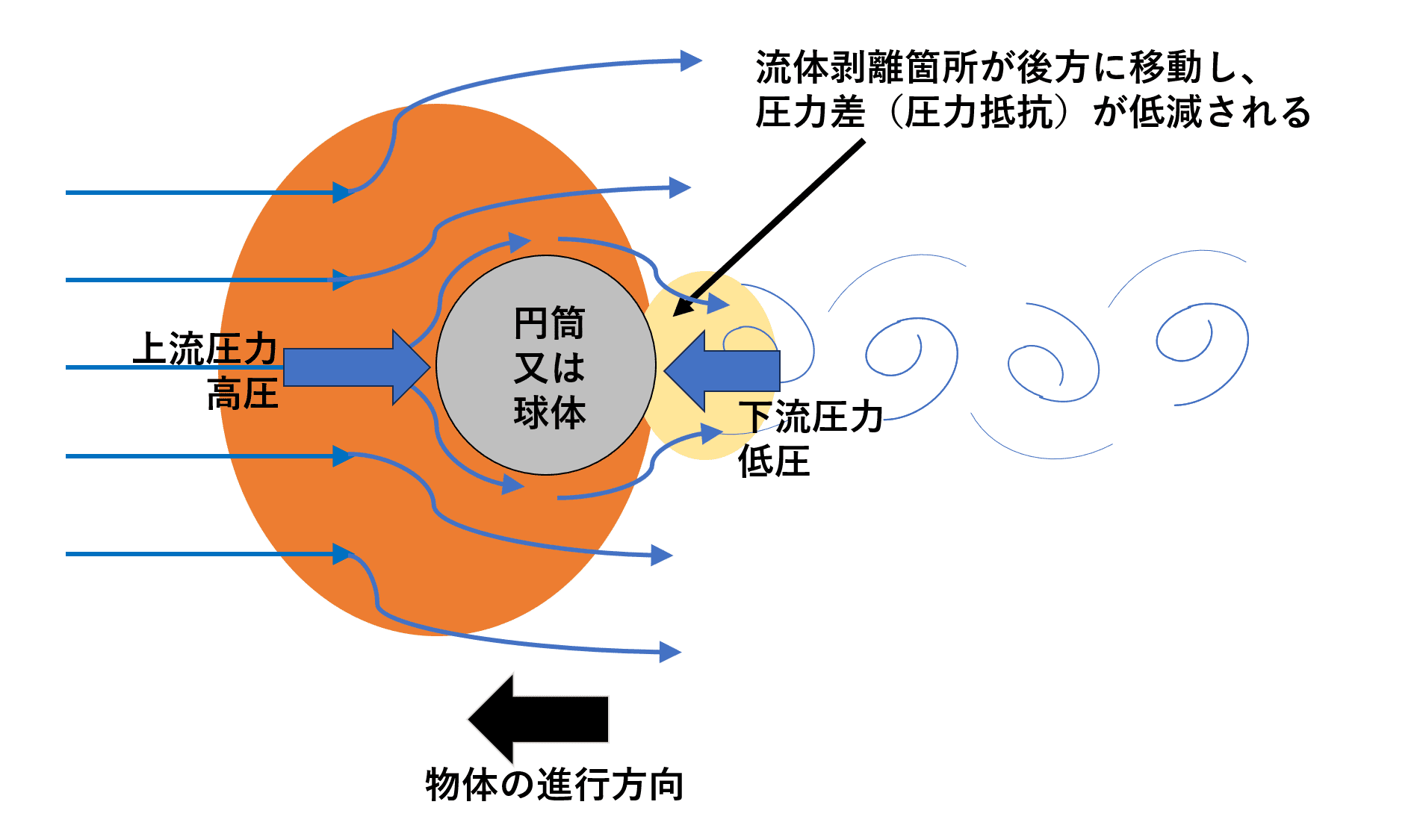
臨界レイノルズ数の時の圧力差低減について

物体が自由落下しても終端速度を超えない

物体が静止流体を自由落下する場合は、どのようになるのでしょうか？

空気中を落下する雨粒や水中を上昇する気泡など、流体中を移動する物体は、その形状や落下速度に応じた抵抗を受けながら移動を続けます。

最終的に重力と抗力が釣り合ったときに一定の速度になり、その速度を終端速度または終末速度と呼びます。

球体の物体の場合の終端速度の計算式を以下に示します。

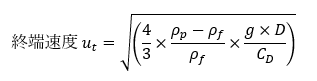
C _D:抵抗係数、ρ _p:球物体の密度

ρ _f:流体の密度、D:球の直径、g:重力加速度

ここでの抗力係数はレイノルズ数が500以上であれば、0.44として計算できます。終端速度によってレイノルズ数が決まるため、繰り返し計算を行い、終端速度を求めることになります。

この計算方法は、物体を球体になぞらえて、終端速度を求める際に使用することができる為、非常に便利な式です。

抗力はどういった場面で利用されているか

空気抵抗を用いる装置として、航空機の空力ブレーキやパラシュートがイメージしやすいかもしれません。

その他、化学工業の分離技術として、粉体やペレットを気流で分離する分級器やサイクロン式分離機にも終端速度を利用しています。

• 流体力学を学ぶ