最近では設計者の構造解析ソフトにおいて、3Ｄ図面から解析モデルを自動的に作ってくれる機能があるため、解析専任者でなくてもCAEによる事前検討が手軽にできるようになっています。

一方でCAEはあくまでも「数値解析理論に基づいた計算結果」でしかなく、解析過程において様々な誤差を含んでいます。

CAE解析が手軽になった反面で、CAEについてあまり詳しくない方が解析を行う場面が増えているように感じます。

このコラムでは、線形の構造解析において誤差が大きくなる要因についてまとめました。

「業務においてCAEは使うけど、どの様な計算をしているか詳しくない」という方はぜひ本記事を参考に、精度の高い解析をするようにしましょう。

構造解析の線形解析とは？

有限要素法

有限要素法（FEM: Finite Element Method）はCAEに用いられる数値解析手法の1つです。

構造や流体、伝熱など様々な解析に用いられますが、特に構造解析分野でこの有限要素法が主に用いられています。

構造解析用のソルバ（条件に基づいて計算を実行して方程式を解くプログラム）としてメジャーな「NASTRAN」や「Ansys」などに加えて、最近の設計現場で用いられることの多くなった「CATIA CAE」などにも、この有限要素法が使われています。

有限要素法は、複雑な形状・性質を持った部材を計算するための小領域に分割し、小領域毎の方程式を組み合わせた全体のつり合い方程式を解くことにより、構造全体の近似解を算出します。

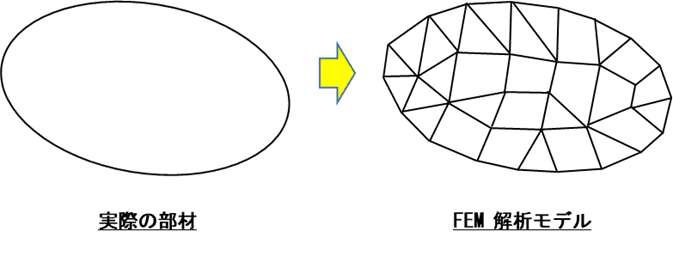
解析モデルを構成する要素には下図に示すように３種類あり、それぞれ「バー：一次要素」「メッシュ：二次要素」「ソリッド：三次要素」と呼ばれています。また、それぞれの要素の頂点を「節点」といい、要素は複数の節点から構成されています。

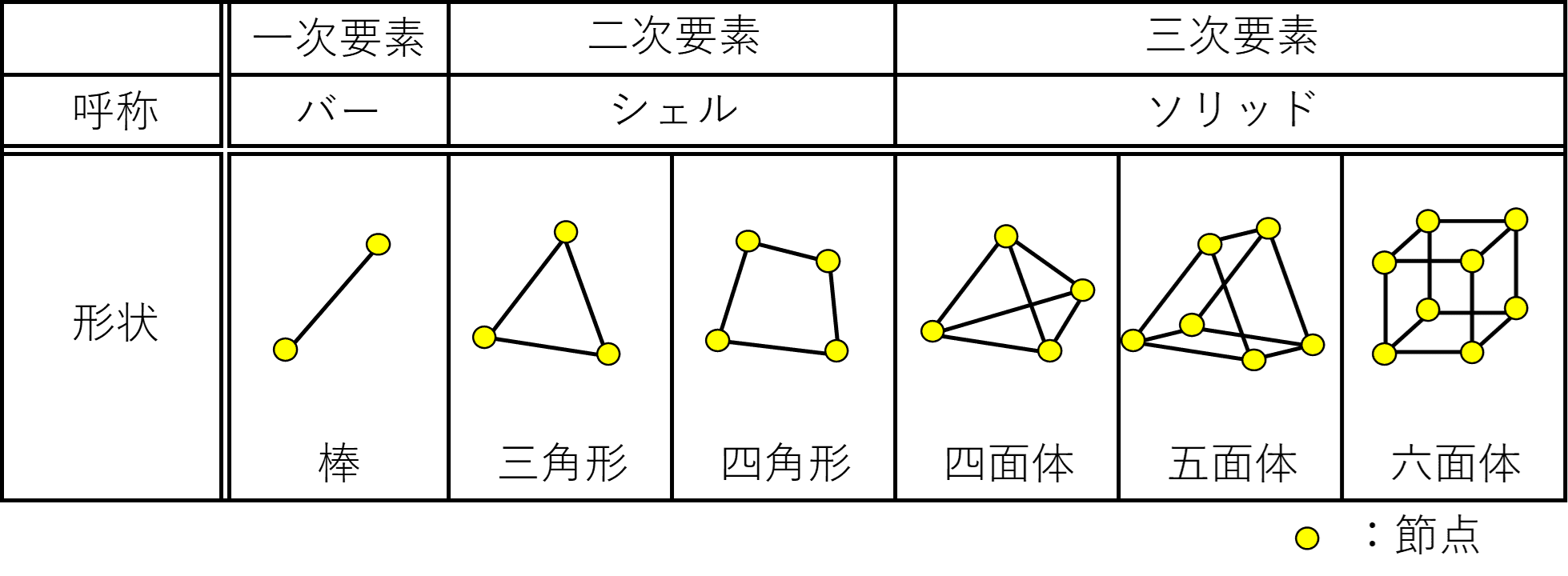
バー要素やシェル要素はそれぞれ「棒材」や「板材」をモデル化するための要素で、三次要素よりも節点数が少ないため、データ量が軽くなるメリットがあります。

しかし解析モデルを作るための中立線や中間面を新たに作る必要があるため、三次元モデルデータにそのまま適用することが出来ません。

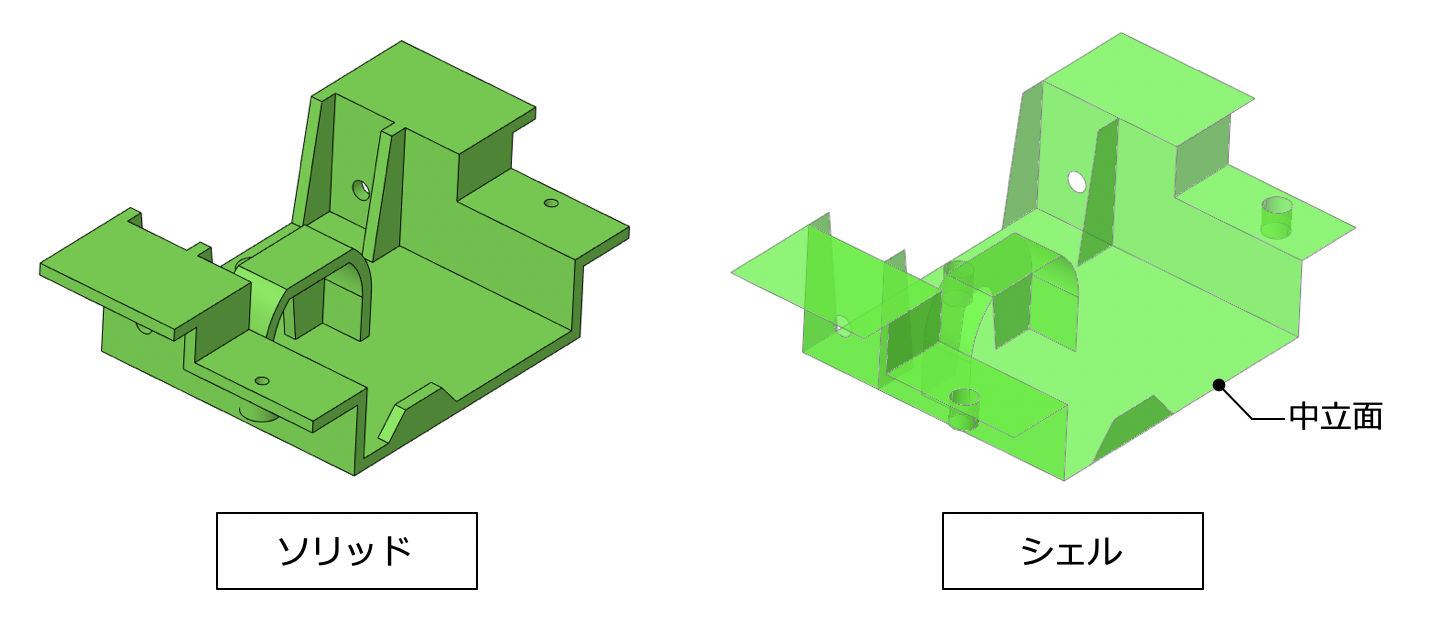
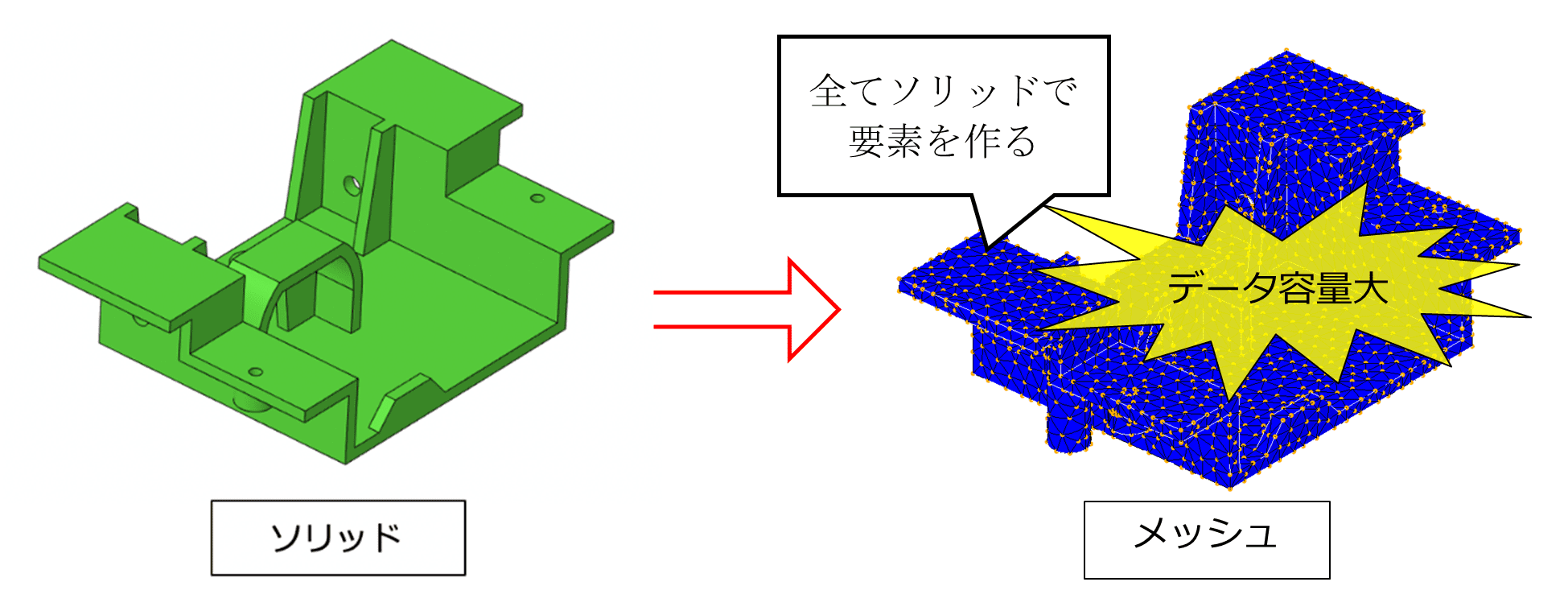
そのため、三次元モデルを用いて直接解析モデルを作成するCAEソフトでは、全ての要素をソリッドモデルで作ることとなってしまい、解析専任者が使用するプリポストで作る解析モデルよりもデータ容量が大きくなってしまう欠点があります。

有限要素法を用いた線形解析理論

有限要素法における線形解析は「仮想仕事の原理」と呼ばれる理論を前提として計算しています。

仮想仕事の原理とは、力がつり合った弾性体が外力によって変位（仮想変位）した時に、外部から受けるエネルギーと弾性体のひずみ（仮想ひずみ）によるエネルギーの総量が等しくなることです。

二次要素における仮想仕事の原理を表す式は以下となります。

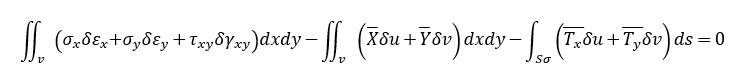
ここで、δεx、δεy、δγxyは仮想ひずみを、δu、δvは仮想変位を示します。

左辺において、第一項が仮想ひずみエネルギー、第二項が外力の体積力による仮想仕事を、第三項が外力の表面力による仮想仕事をそれぞれ表しています。

「仮想仕事の原理」は、要素毎の剛性マトリックスの導出に用いられます。

構造解析における線形解析

構造解析における線形解析とは、負荷した「荷重」と部材の「変位量」が比例する解析のことを指します。

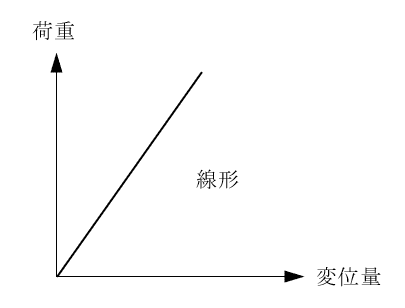
線形解析では、各節点に働く荷重：Fと変位量：Uの関係式は構造物の剛性：Kを含めて以下で表されます。FEMにおいて構造物は複数の節点で構成されるため関係式は行列式となります。

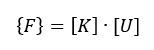
線形解析は微小変形解析とも呼ばれています。上式の線形性が成立するには「①荷重と変形量が比例する材料特性を有する」「②変形後の荷重のつり合い変化が無視できるほど変形量が微小」という前提を置く必要があります。

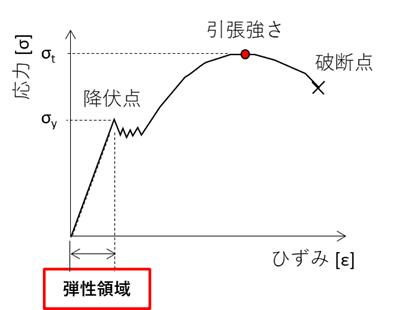
つまり、①は材料が降伏しない範囲（弾性領域）であることを、②は変形量が小さいことをそれぞれ示しており、この前提のことを微小変形理論と呼びます。

微小変形理論が原因となる誤差

前章で線形解析は微小変形理論を前提としていることを述べましたが、部材の形状によっては微小変形理論が適用出来ず、大変形解析という非線形解析を行う必要がある場合があります。

このような部材では線形解析を行っても誤差が大きく実現象を再現出来ないため、解析者はどの様な場合に大変形となるかを事前に知っておくことは重要です。

大変形には「大ひずみ」「大回転」「ストレススティフニング」の３つがあり、それぞれ線形解析が適用出来ない原因が異なります。

以下に具体的にどのような場合に線形解析が適用出来ないのかを見ていきましょう。

大ひずみ

大ひずみはひずみが大きく発生する解析時に考慮する必要がある幾何学的非線形です。

下図のように引張荷重を受ける部材のひずみが大きくなり変形量が過大になると、変形前後で荷重が受け持てる断面積が小さくなってしまい、部材の剛性が小さくなってしまいます。

大ひずみが発生した場合の応力・ひずみを「真応力」「真ひずみ」、発生前の応力・ひずみを「公称応力」「公称ひずみ」として区別しています。

下図に公称応力と真応力を比較した、応力-ひずみ線図を示します。

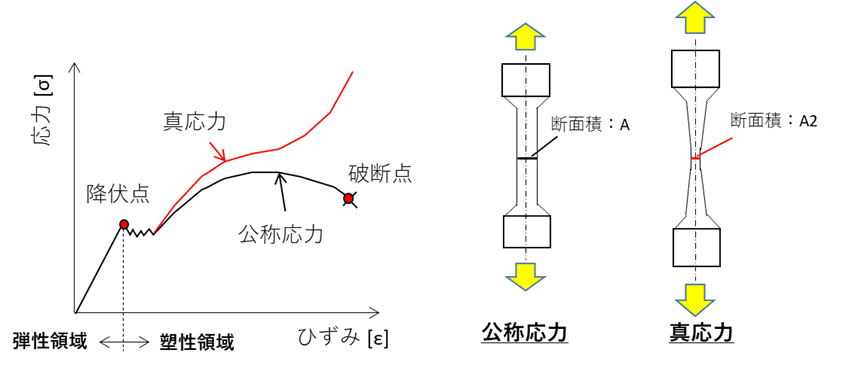
弾性領域である降伏点までは公称応力と真応力は同じですが、塑性変形が進んでいきひずみ量（変形量）が増大すると断面形状差が大きくなるため、実現象との差が増大していきます。

線形解析は弾性領域内での解析であるため、そもそも塑性領域内での誤差が大きくなる大ひずみ問題は解かないことが前提ですが、最大応力が降伏点付近となるような、ひずみ量が過大な解析をする場合には注意するようにしましょう

大回転

大回転はひずみ量が小さくても、回転量が大きい場合に考慮する必要がある幾何学的非線形です。

下図に大回転を考慮しない場合の一次要素が剛体回転した場合の、各方向におけるひずみ量を示します。

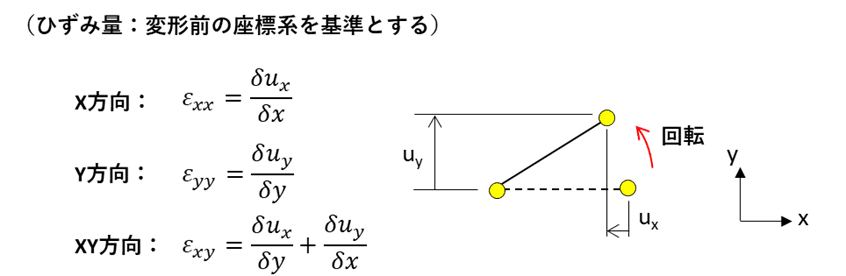
図から分かるように一次要素は回転をしているだけで変形しないため、この要素に発生するひずみ量は0のはずですが、変形前の座標系を基準とするとひずみが発生してしまいます。

したがって、一次要素と共に回転する座標系を基準としてひずみを計算する必要があり、この機能を大回転と呼びます。

大回転は大ひずみと一緒に考慮されて解析を行うことが一般的です。

ストレススティフニング

ストレススティフニング(Stress Stiffening)は、面内応力によって面外剛性が影響を受ける幾何学的非線形です。

面内に受ける引張荷重が増加するにしたがって、面外剛性は上昇します。これはギター弦の張力を上げることにより弦の面外剛性が向上し、固有振動数が上がる現象などがよく知られています。

逆に、圧縮の面内力を受けると面外剛性は低下します。

これは航空機におけるビームカラムを解析する場合にあたります。

解析モデルが原因となる誤差

有限要素法を用いたCAE解析の誤差には、数値計算が原因の誤差、離散化が原因の誤差、解析モデルが原因の誤差の3種類があります。（「機械のための有限要素法入門」：川井忠彦、岸正彦著を参照）

この中で「数値計算が原因の誤差」と「離散化が原因の誤差」は、解析担当者が操作出来ない範囲であるため、本章では「解析モデルが原因の誤差」について以下に記載します。

要素の形状による誤差

解析モデルが原因の誤差の1つに「要素の形状による誤差」があります。

要素の形状とは、要素自体の形状のことです。

有限要素法における要素形状には三角形や四角形などがありますが、それぞれ「正三角形」や「正四角形」に近い形状の方が精度は高くなります。(下図参照)

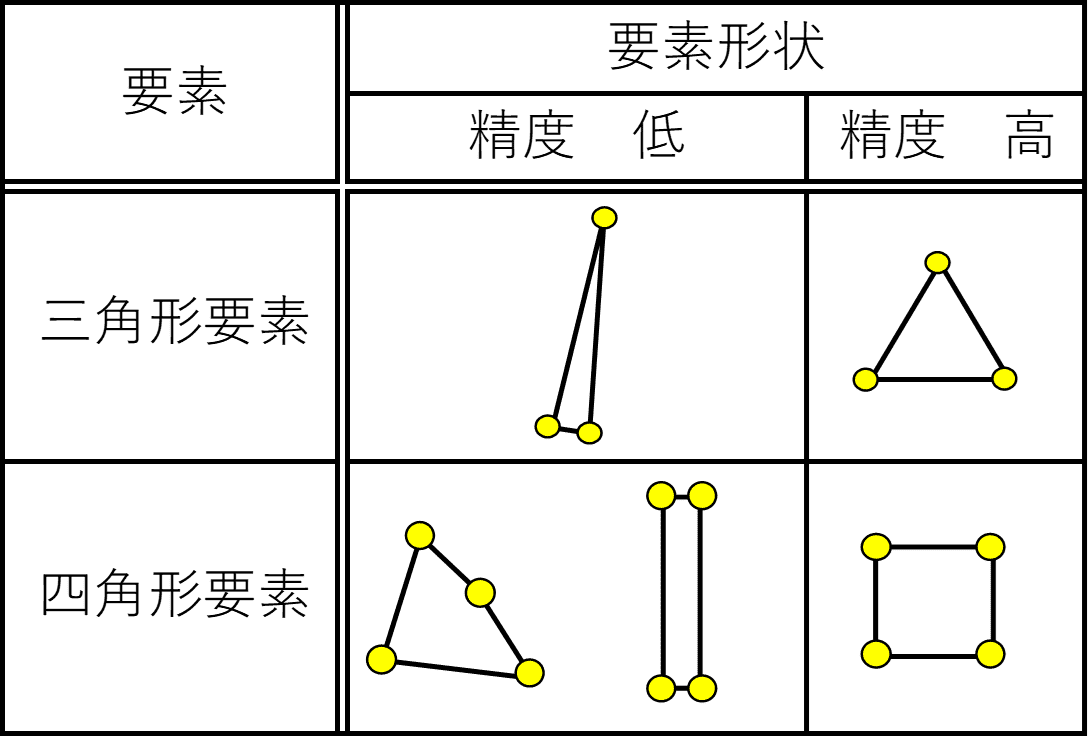
上図の左の要素のように「形が悪い要素」を用いて解析をすると、その要素だけが周囲の要素よりも高い応力が発生するような不自然な結果となってしまいます。

最近のプリソフトにおける自動で要素を切る機能は高性能であるため、自動で切ってもある程はきれいに切ることが出来ますが、要素を切った後は必ずアスペクト比（縦横の辺の長さの比）を確認するように心がけましょう。

要素の大きさによる誤差

解析モデルにおいて、一般的に要素の大きさが小さければ小さいほど精度は良くなります。

これは有限要素法が、下図のように直線によって近似される手法であることからも明らかです。

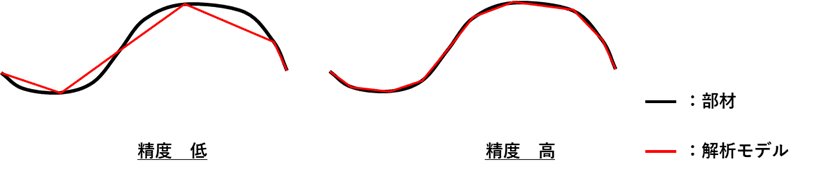
ただし要素の数を増やすと精度が上がる反面、解析時間が増大します。

またある程度の数まで要素数を増やすと、下図のように解析結果の誤差は飽和するため、解析時間と精度を踏まえた適切な要素数を把握する必要があります。

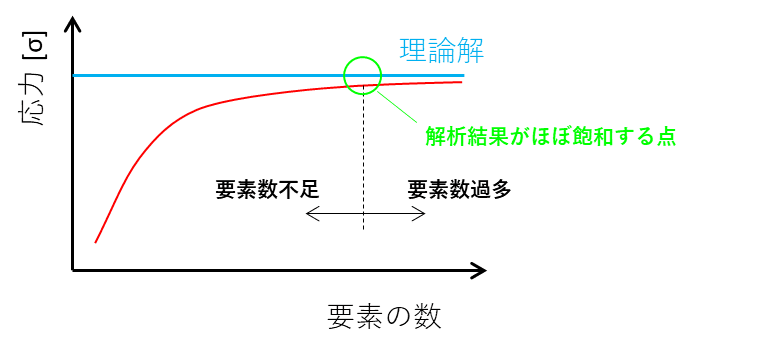
経験の少ない現象について解析を行う場合には、複数の要素数を用いたモデルで解析精度が担保されているかを確認するようにしましょう。

また一般的に、荷重が負荷される点や応力集中部だけの要素数を多くしても高い精度が出るため、モデル全体の要素を細かくするのではなく精度が必要な箇所の要素を細かくするのも効果的です。

要素の種類による誤差

有限要素法では、要素の種類によって解析精度に差が出ます。

要素の種類による精度の差には2つあり、1つ目は形状による差で、2つ目は次数による差です。（下図参照）

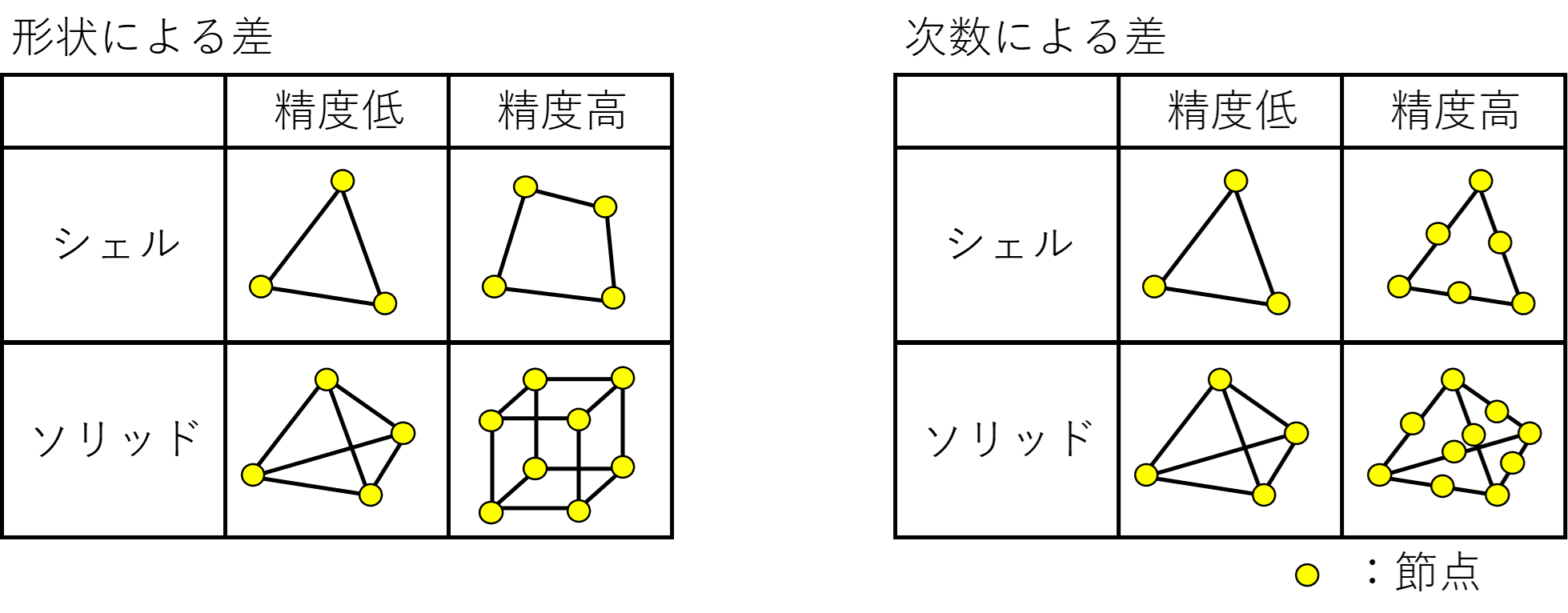
形状による差は、同じ次数の要素であっても三角形や四面体要素よりも四角形や六面体要素の方が、精度が高くなります。従って、解析モデルを作る際には出来るだけ四角形や六面体だけでメッシュを切るようにすると精度が高くなります。

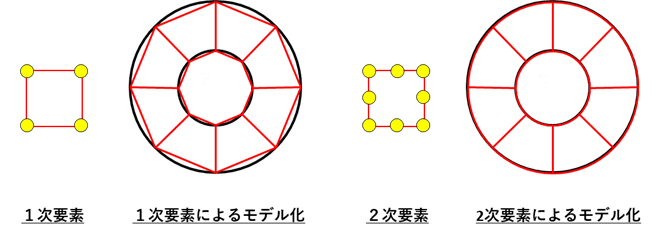
次に次数による差とは、要素の節点間で近似できる物理量の次数を増やす方が、精度がよくなることです。

下図のように、節点間を二次関数で近似出来る二次要素の方が、線形近似する一次要素よりも精度が高くなります。

拘束条件による誤差

構造解析では、解析する部材について6自由度を固定する必要があります。

6自由度とは、X、Y、Z、RX、RY、RZの6方向のことで、部材のどこかの点を固定しないと、解析モデルに荷重をかけた時に反力が取れず、収束しないためです。

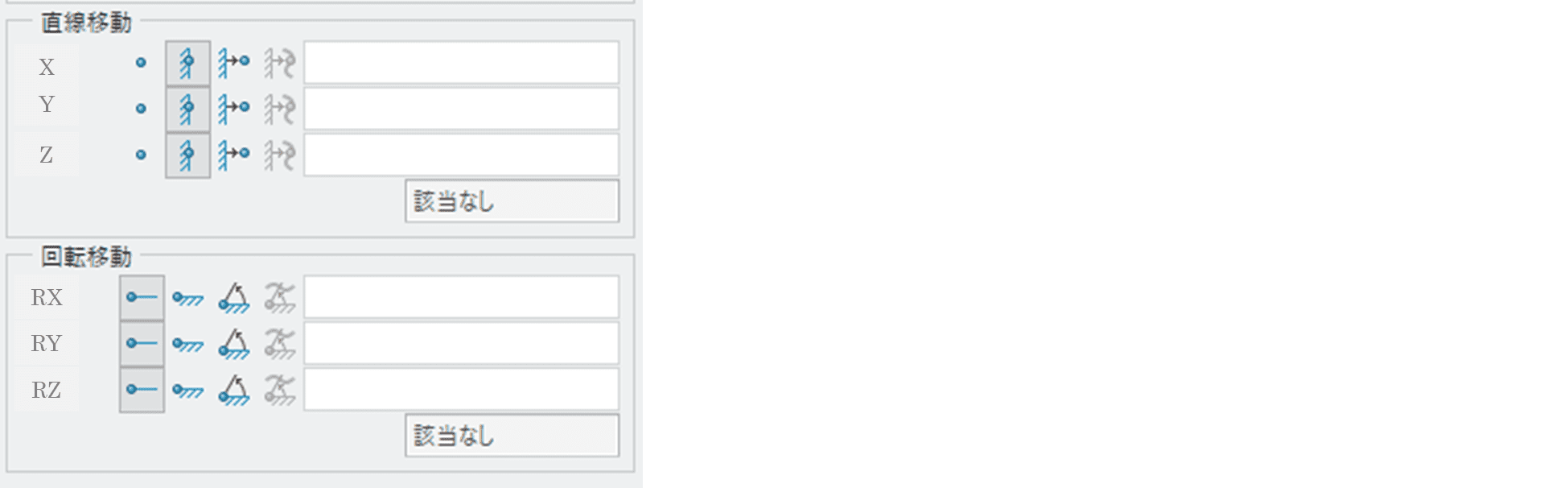
拘束条件には①支持なし、②固定の2種類しかありません。

しかし実際の形状はその中間の剛性で支持されているため、実現象と解析結果との間に誤差が生じてしまいます。

構造解析ではこのような拘束部において最大応力や最大変位が発生するため、過去の経験に基づいて拘束部の応力値や変位値は強度評価には含めないなどの対策をとる必要があります。

また部品単体で評価する場合に、締結部を固定するのではなくバネ要素を入れることで、締結部品の疑似的な剛性値を模擬することも出来ます。

荷重の設定による誤差

荷重の設定方法によって誤差が発生する場合があります。

例えば、下図のように緑線の部材から、円形の物体に荷重が負荷された場合を考えます。

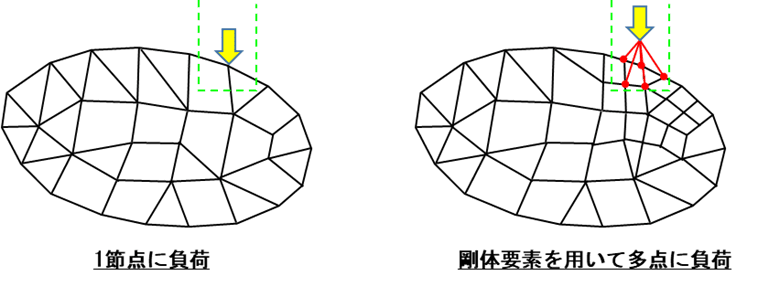
左図では、解析モデルにおける緑部材の範囲が1節点しかないため、1点に荷重を負荷しています。

しかし荷重負荷点を1節点のみとすると、要素数を増やした時に荷重負荷点まわりの応力値が過剰に出てしまうことがあります。

したがって右図のように緑部材内の節点を増やして剛体要素でつなぎ、複数の節点に荷重を負荷するようにする方が適切と言えます。

このように荷重を分散すると、過剰な応力が発生しないようになります。

応力特異点

線形解析において、応力集中や集中荷重が発生する点は正しく計算出来ず、このような点のことを応力特異点と呼びます。（下図参照）

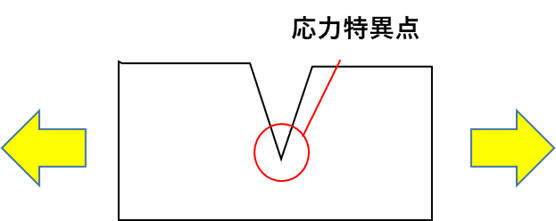
応力特異点では応力の理論値が無限大となるため、要素数を増やしていくと応力値が際限なく増えてしまいます。

特異点でない箇所では要素数を増やしていくにつれて、次第に理論値に飽和していくため、要素数を増やしても一向に応力値が飽和しない場合は特異点を疑う必要があります。

特異点の対策には、「①特異点近傍の応力を無視する。」「②特異点に小さなRを付けることで、応力集中を回避する。」などがあります。

以上、本コラムでは線形解析において誤差が大きくなる要因として以下について説明してきました。

・微小変形理論が原因となる誤差
  大ひずみ
  大回転
  ストレススティフニング
・解析モデルが原因となる誤差
  要素の形状による誤差
  要素の大きさによる誤差
  要素の種類による誤差
  拘束条件による誤差
  荷重の設定による誤差
  応力特異点

これらの誤差を含んできることをよく理解したうえで、必要に応じて対策を取りながら上手にソフトを利用していくことが大切になります。

• CAEを学ぶ