「エントロピーとエンタルピーって何だったっけ？」

「名前が似ているから、いつもどちらがエンタルピーの値なのかいつも忘れてしまう」
蒸気のエントロピーとエンタルピーについては、むかし熱力学で習ったけど、もう忘れてしまったという人も多いのではないでしょうか？

蒸気は多くの工業プロセスや発電所でのエネルギー変換を行うための媒体として、重要な役割を果たしています。その中でも、蒸気タービンは、発電所や産業プラントなどで広く利用されているエネルギー変換装置です。

特に火力発電所では、ボイラーで生成された高温高圧の蒸気を用いてタービンを回転させ、その運動エネルギーを電力に変換する役割を担っています。

蒸気タービンの効率と性能は、エネルギー資源の有効利用や環境負荷の軽減に直結するため、その設計と運用は非常に重要です。タービン内での蒸気の挙動を理解するためには、エンタルピーやエントロピーといった熱力学的な概念が不可欠です。

エンタルピーとエントロピーは全く意味が違う

エンタルピーとエントロピーは、名前が似ていますが、その概念は全く違います。

簡単に説明すると、エンタルピーは、システム内のエネルギーの動きを計算する際に用いられます。
※エネルギーの動きの計算とは、蒸気がある状態から変化する際に、どれだけのエネルギーが移動したか（仕事に変換されたか）を考える際に使用されます。

一方、エントロピーは、システムの乱雑さの程度を表し、理想的な条件下でのエネルギー変換効率を評価する指標となります。特に蒸気タービンでは、エントロピーが一定である等エントロピー変化が理想モデルとして使用されます。

このモデルは、実際のタービンの性能を評価する基準として用いられ、効率的なエネルギー変換を目指すための設計指針となります。

エンタルピーとエントロピーとは何なのかについてもう少し詳しく説明します。

エンタルピー（Enthalpy）とは

エンタルピーとは、その物体が持つエネルギーの総量の一部であり、物体が持つ内部エネルギーと膨張や圧縮を行うためのエネルギーの和を指します。

単位はJ（またはcal）で表されます。文献に記載している数字は大抵「キロ」の単位が付いたkJやkcalの単位を使っていますので注意してください。

また、単位質量当たりの物体の持つエネルギーは比エンタルピーと呼ばれ、その単位はkJ/kgやkcal/kgで表します。蒸気表や文献では、この比エンタルピーの方が目にする機会が多いかもしれません。

ちなみに参考書などでは、エンタルピーの値は「H」、比エンタルピーの値を「h」と表記しているのが一般的です。

様々なエンタルピー

エンタルピーは工業の分野で様々な呼び名で利用されています。
その一部を紹介します。

①燃料の高位発熱量と低位発熱量

燃料から取り出せる熱量（エネルギー）を換算するために、使用する値です。燃料を燃焼すると、その化学変化により水が発生します。高位発熱量と低位発熱量の違いは、燃焼中に発生する水分が蒸気に変化するための熱量（蒸発潜熱）を含んでいるかどうかです。

• 高位発熱量・・・蒸発潜熱を含む
• 低位発熱量・・・蒸発潜熱を含まない

高位発熱量は、熱量計で計測・算出された値を示します。その値から蒸発潜熱を差し引くことで低位発熱量の値になります。

熱の利用を考える際は、この低位発熱量を利用する場合が多く、燃焼ガス温度の計算には通常、低位発熱量が用いられます。
※燃料仕様に「発熱量」としか記載がない場合は、必ず高位発熱量なのか低位発熱量を確認するよう要しましょう。

②標準生成エンタルピーと標準燃焼エンタルピー

標準生成エンタルピーは、標準状態 (1atm、25℃) において、1 mol の化合物を生成するときに生じるエンタルピーの値です（標準生成熱とも呼ばれます）。また、標準燃焼エンタルピーは、標準状態において、その物質 1 mol が酸素と反応して燃焼するときの反応エンタルピーの値です。

この２つは、化学反応における、反応前後のエンタルピー変化をヘスの法則で求めるときに使用する値です。

エンタルピーと内部エネルギーの違い

ここで「内部エネルギーとエンタルピーの違いがよく分からない」という疑問を持っている方も多いのではないでしょうか？

内部エネルギーとは、物体が自分自身の中に持っている熱エネルギーのことです。このエネルギーは、外から熱を与えたりしない限り変化しません。

一方、エンタルピーの式は、内部エネルギーを用いると以下の式で表します。

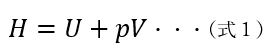
H:エンタルピー、U：内部エネルギー、pは圧力、Vは体積

エンタルピーの変化量は、以下の式となります。

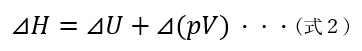
この式だけでは、エンタルピーの値に何の意味があるのか、なかなか伝わりませんね。
この式を、以下の式に読み替えてみます。

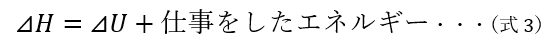
すると、以下のことを認識できるようになります。

• 内部エネルギーは、「入熱や放熱による物体の温度変化」が関係している。
• エンタルピーは、「内部エネルギーの値に、入熱や放熱によって生じる熱以外のエネルギー（仕事量）」も含んでいる。

例えば、しぼんでいる風船を外部から温める場合について考えてみると、加熱による温度上昇は内部エネルギーに含まれます。一方で、エンタルピーの値には、内部エネルギーの値と風船が膨らむという仕事を足し算した値となります。

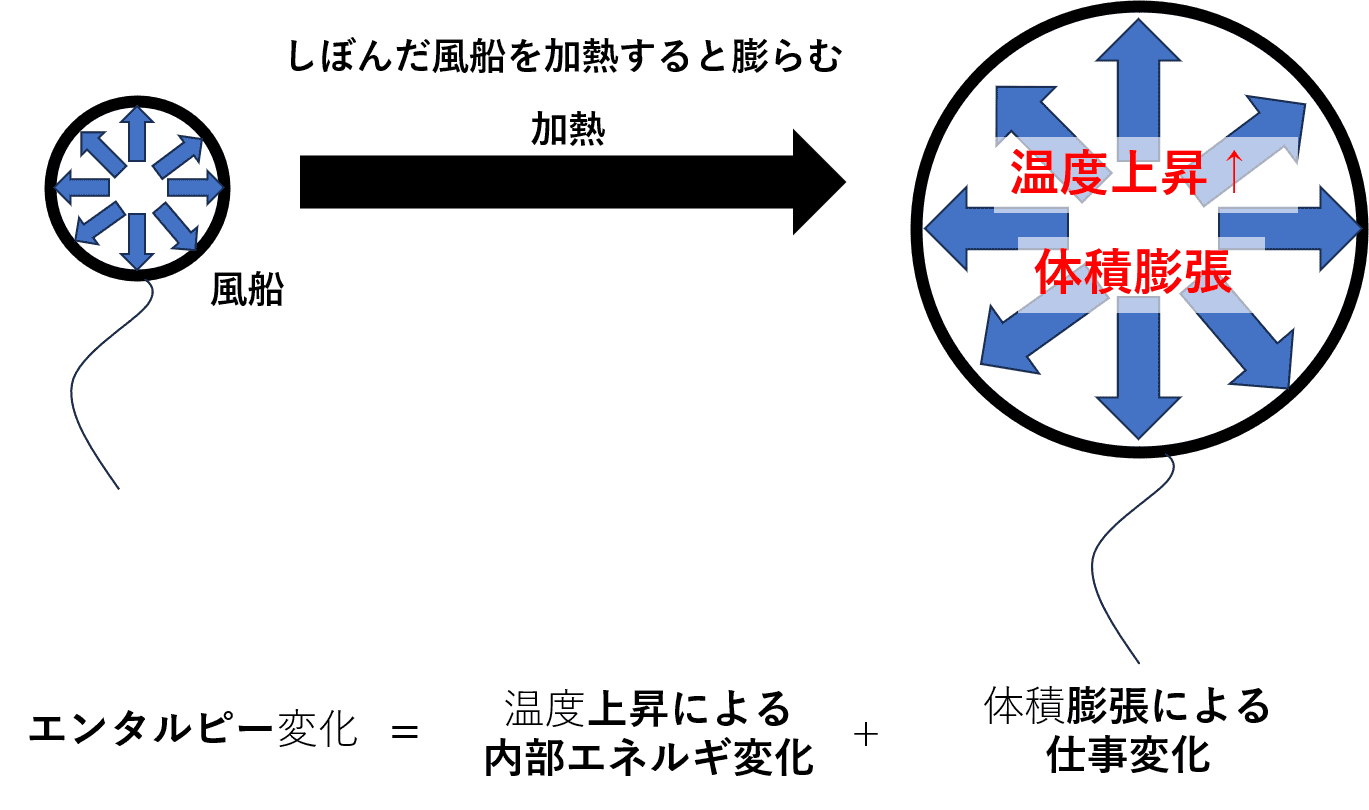
さらに、圧力が一定で変化する場合は、熱力学第１法則の式と組み合わせることで、エンタルピーの変化はシステムが吸収または放出する熱量に等しくなります。

圧力一定での変化なので、

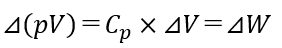
が成り立ちます。

これを式２に代入すると、

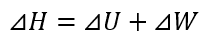
となり、式３を表す式となります。

この式は意味することは、

ある物質に熱を加えて、その内部エネルギーの変化（温度変化により）を計測できるのであれば、エンタルピーの変化量⊿Hから、その物質がどれくらいの仕事をしたのかを算出することが出来るようになるのです。

例えば、ボイラー内の水を蒸気に変換する際のエネルギーの総量は、エンタルピーを用いてで計算するとどうなるでしょうか？

例：大気圧下の10kgの飽和水（沸騰し始める状態の水）を飽和蒸気にするには、どれくらいの熱量を与えればよいかを求めてみます。

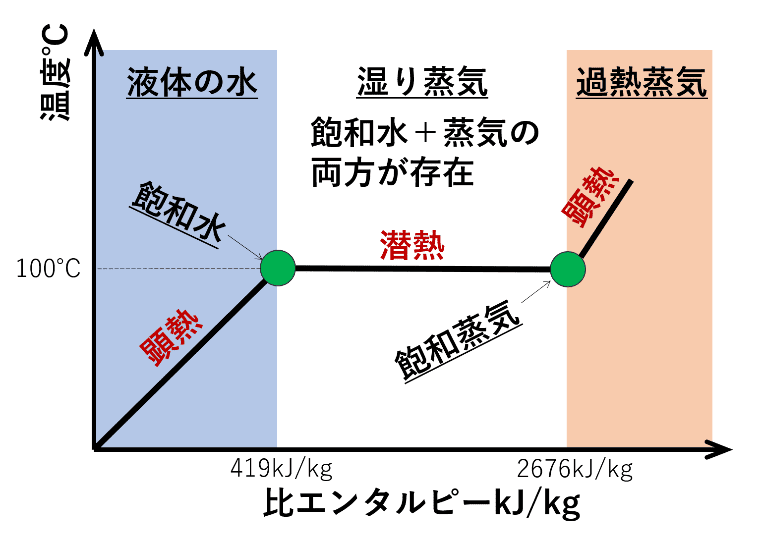
まず、飽和水と飽和蒸気の比エンタルピーはそれぞれ水の蒸気表より

• 飽和水の比エンタルピー：419kJ/kg
• 飽和蒸気の比エンタルピー：2676kJ/kg

と分かっています。飽和水から飽和蒸気までは温度変化は無いので内部エネルギーの変化⊿Uは0です。

それぞれのエンタルピーを求めると、以下の式で飽和水に与える熱量を求めることができます。

エンタルピーは、エネルギーの移動や変換を考慮する際に非常に便利な量なのです。

エントロピー（entropy）とは

エントロピーとは、系の乱雑さや無秩序の程度を表す物理量です。エントロピーの変化は、次のように定義されます

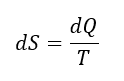
dS：エントロピーの変化、dQ：熱の移動量、Ｔ：絶対温度

エントロピーを活用する場面の多くは、等エントロピー変化を考えたいときに用いることが多いです。

等エントロピー変化とは以下の特徴があります。

1. 断熱性がある（熱のやり取りがない）
2. 可逆性がある（現実には存在しない理想的な状態変化である）
3. ガスタービンや蒸気タービンを通して圧縮や膨張される場合は、等エントロピー変化（isentropic process）が理想となる

③が起こる理由としては、蒸気タービン内では、蒸気が断熱的に（熱の出入りなしに）膨張します。その際は外部との熱交換がないことが理想であるため、エントロピーは一定に保たれると仮定されます。

蒸気圧曲線を知ろう

蒸気圧曲線は、圧力と温度の関係を示すグラフです。この曲線の上側の領域は、飽和蒸気圧を超えた分は液体で存在し、下側の領域は蒸気（気体）となることを示しています。

このグラフは、物質が何℃でいくらの圧力になると蒸気になるか（または液体になるか）を表す曲線である為、液体の沸点を確認する際に使用することが多いです。

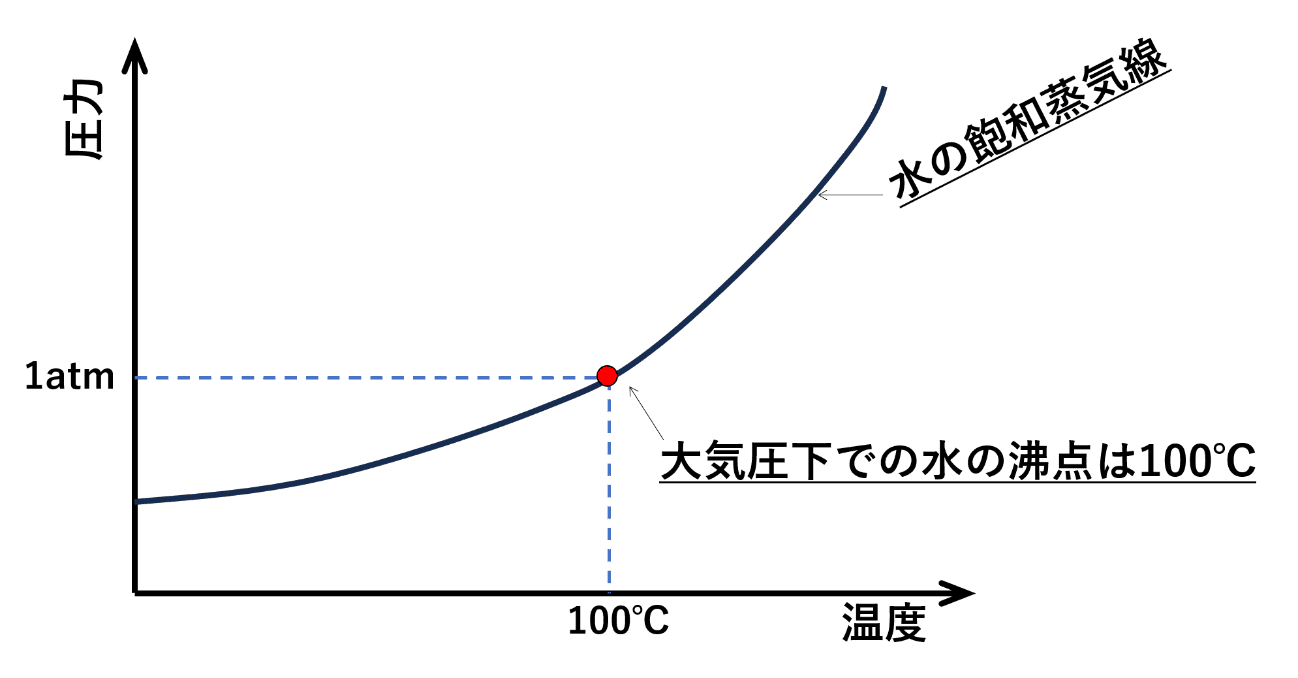
この曲線を見て、「水が蒸気になる場合、一瞬ですべて蒸気になる」と勘違いしてしまいそうになりますが、実際は蒸気になる際、水と蒸気が混ざった状態になります。

この水と蒸気が混ざった状態を理解するためには、圧力とエンタルピーのグラフ（P-H線図）を理解し、以下の2つの重要な線を理解しておきましょう。

• 飽和液線: このライン上は水が飽和水の状態（すべて水）にある点を示す。
• 飽和蒸気線: このライン上は蒸気が飽和蒸気の状態（すべて蒸気）にある点を示す。

下に圧力とエンタルピーの関係（p-H線図）のグラフを示します。図中の青い線は、気化器や蒸発器の装置で等温変化させる際の線を表しています。

飽和水の線と飽和蒸気の線で囲まれた白色の部分を見ると、圧力を一定で加熱し、飽和水から飽和蒸気に変化させても、温度も変わらないことになります。

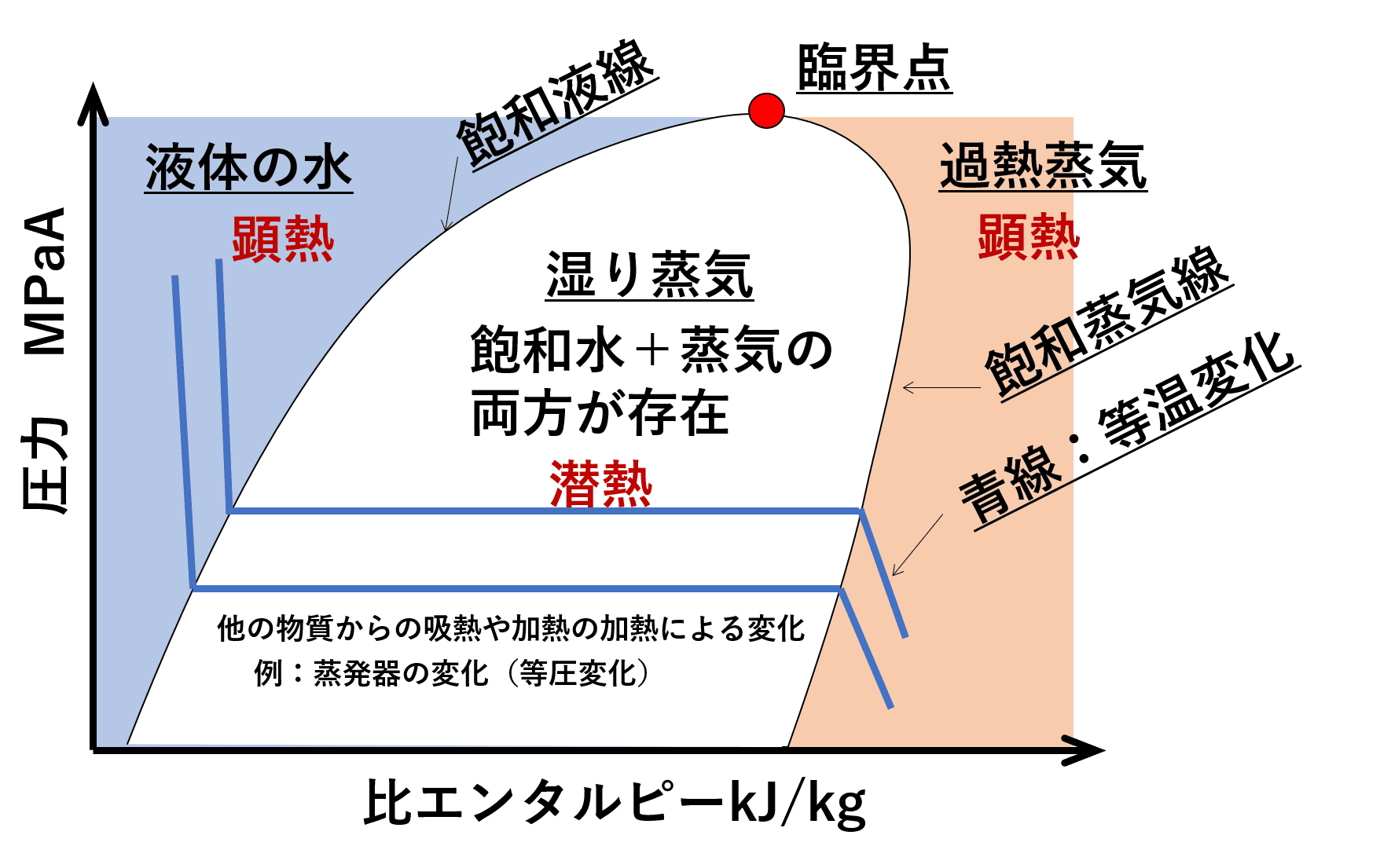
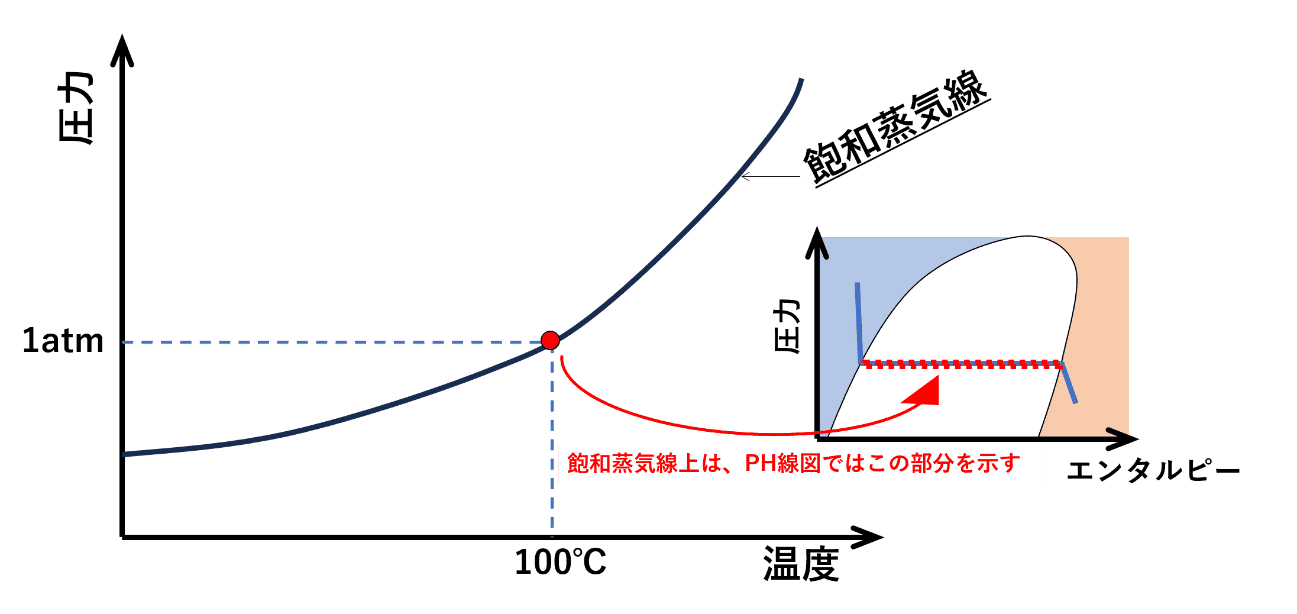
この温度も圧力も変わらない状態（白色領域の青線上の変化）というのが、飽和蒸気圧曲線の線上で起きていることになります。

まとめ

エントロピーとエンタルピーについて理解が深まりましたでしょうか？

飽和蒸気曲線の理解は、蒸気を活用した発電システムや工業的な利用においてとても重要な役割を果たしています。

これらの基本的な理解をもとに、蒸気のエンタルピーとエントロピーを活用して、様々な工業プロセスやエネルギーシステムを効率的に設計・運用することが求められているのです。