投稿日:2023年03月13日

本記事では、軸受寿命の検討方法について紹介します。
これから軸受の選定をする方や軸受寿命の計算を復習したい方にとって、本記事を読むことで軸受寿命の計算が理解でき、使用条件に合った最適な軸受の選定ができるようになります。
軸受寿命とは
軸受を使うといつかは疲労破壊が起きることがあります。疲労破壊が起きると軸受内部で接触する部品の表面の一部が突然うろこ状に剥がれることがあります。
これをフレーキングと呼び、フレーキングが起きるまでの軸受の総回転数を「軸受寿命」と定義しています。
図1.フレーキング(深溝玉軸受の内輪)
引用元:https://www.ntn.co.jp/japan/products/care/damage/rah-rahking.html
軸受寿命の規格は国際規格ISO218で規定されており、都度更新されています。日本ではISOに準拠する形でJISB1518(転がり軸受-動定格荷重及び定格寿命)が規定されています。
軸受寿命を迎えるとどうなる?
先に述べた通り、軸受寿命を迎えると転動面にフレーキングが発生します。フレーキングが発生すると異音や振動が大きくなっていくとともに、破損の進行が大きくなり、最終的には周辺部品が焼付き、回転機器がロックするなどの可能性があります。
そうならないように、適切な軸受寿命を算出して、軸受が故障する前に交換できるよう、メンテナンス期間を設定する必要があります。
軸受寿命には確率が伴う
まったく同じ仕様の軸受を同じ条件で運転しても、全ての軸受が「同時に壊れる」ことはありません。
軸受寿命には大きなばらつきがあることが分かっており、同時に複数個の軸受を運転しても、そのうちの最長寿命は最低寿命の50倍から100倍の差があると言われています。
そのため、軸受の寿命は保障できるものではなく、確率分布から「何%の信頼度」という形で決められています。確率分布は寿命試験の結果から、ワイブル分布が適用されています。
ワイブル分布は寿命の絶対値とばらつきの大きさによって曲線が決定される性質を持っており、軸受の場合は下図のような曲線を描く傾向にあります。
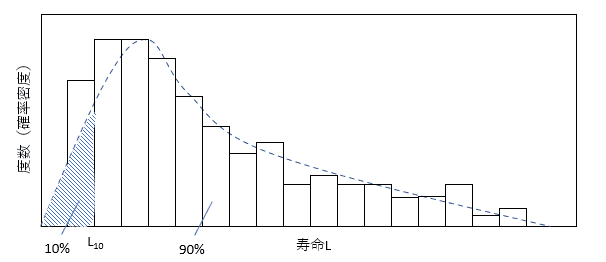
図2.軸受寿命の分布の例
軸受寿命計算の式
軸受寿命の計算式は、玉軸受と、ころ軸受で異なり、次の式(1)(2)で表されます。
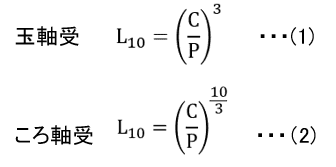
ここでL10とは信頼度90%の基本定格寿命と定義されています。同じ軸受を100個、同じ条件で回転させたときに、10個(10%)壊れるまでの寿命という位置づけです。L10の単位は×106回転になりますので、L10=1の場合は100万回転となります。
Cは基本動定格荷重と呼び、軸受けを100万回、回転させたときに「10%の確率でフレーキングが発生する荷重」を示します。Cの値は軸受を構成する部品の設計によって変わるため、メーカが計算してカタログに記載しています。
Pは軸受に掛かる荷重です。円筒ころ軸受のようにラジアル方向のみに荷重が作用する場合は、荷重をそのままPに代入します。しかしラジアル方向の他にアキシャル方向にも荷重が作用する玉軸受けは以下の式(3)でPを求めます。
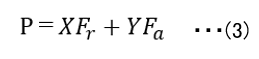
Fr:ラジアル方向の荷重
Fa:アキシャル方向の荷重
XとYはCと同様にメーカの軸受設計によって異なるため、選定するメーカのカタログから算出します。
なお、回転速度が一定の場合、軸受寿命は回転数ではなく、運転時間Lh(時間)として表す場合が多いです。運転時間を求める式に変形すると以下の式(4)(5)になります。
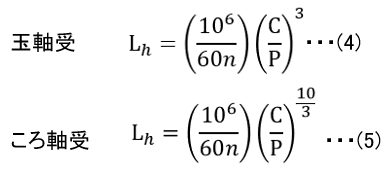
CとPの単位はN(ニュートン)です。
「L10は信頼度90%」の話に戻します。
使用する機械によっては「10%も壊れると困る」という意見があると思います。顧客第一に考えると、1台も壊れてはいけないと考えるのは当然のことでしょう。
ただ、軸受にかかわらず、どのような事象にも「100%」はありえないのかもしれません。決して腹をくくって欲しいと言うわけではありませんが、何%までの信頼度で軸受寿命を扱うか決める必要があります。
一方で、軸受用鋼材の改良により、疲れ寿命も伸びてきています。弾性流体による潤滑理論の研究によって、軌道と転動体との接触部における潤滑油膜の厚さが疲れ寿命に影響することが解明されてきました。
そこで、これらを疲れ寿命計算に反映させるために、下記の補正係数を用いて基本定格寿命を補正する式(6)がISOで定義されるようになりました。
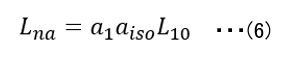
ここで
Lna:信頼度、材料の改良、潤滑条件などを考慮した疲れ寿命
L10:信頼度90%の基本定格寿命
aiso:統合方式に基づく修正寿命係数
a1は信頼度(%)に応じて変化する係数のことです。最大99.95%までの信頼度が定義されており、信頼度が増えることによって以下の表の通り係数が小さくなっています。
表1.信頼度係数a1
| 信頼度、% | a1 |
| 90 | 1 |
| 95 | 0.64 |
| 96 | 0.55 |
| 97 | 0.47 |
| 98 | 0.37 |
| 99 | 0.25 |
| 99.2 | 0.22 |
| 99.4 | 0.19 |
| 99.6 | 0.18 |
| 99.8 | 0.12 |
| 99.9 | 0.093 |
| 99.92 | 0.087 |
| 99.94 | 0.08 |
| 99.95 | 0.077 |
aisoは軸受の疲労源荷重、潤滑状態、運転環境、運転時の汚染粒子、取付け時の洗浄度によって影響する係数です。
続きを読むには…
このページは 会員限定です。申し訳ございませんがお客様の権限では続きをご覧頂くことができません。続きは、会員登録(無料)してご覧ください
個人・企業・学校等60,000人が登録
MONO塾の無料会員になると、サイト内にある人気コラムなどすべてのコンテンツが読み放題です。学習に役立つテキスト全18シリーズも無料でダウンロードいただけます。
会員の方はログイン
あなたにおすすめのeラーニング
- 【全32種類の機械要素を動画で学ぶ!全10章(350分)】
機械要素を学ぶことで自然と「部品選定および設計能力」が身につく












