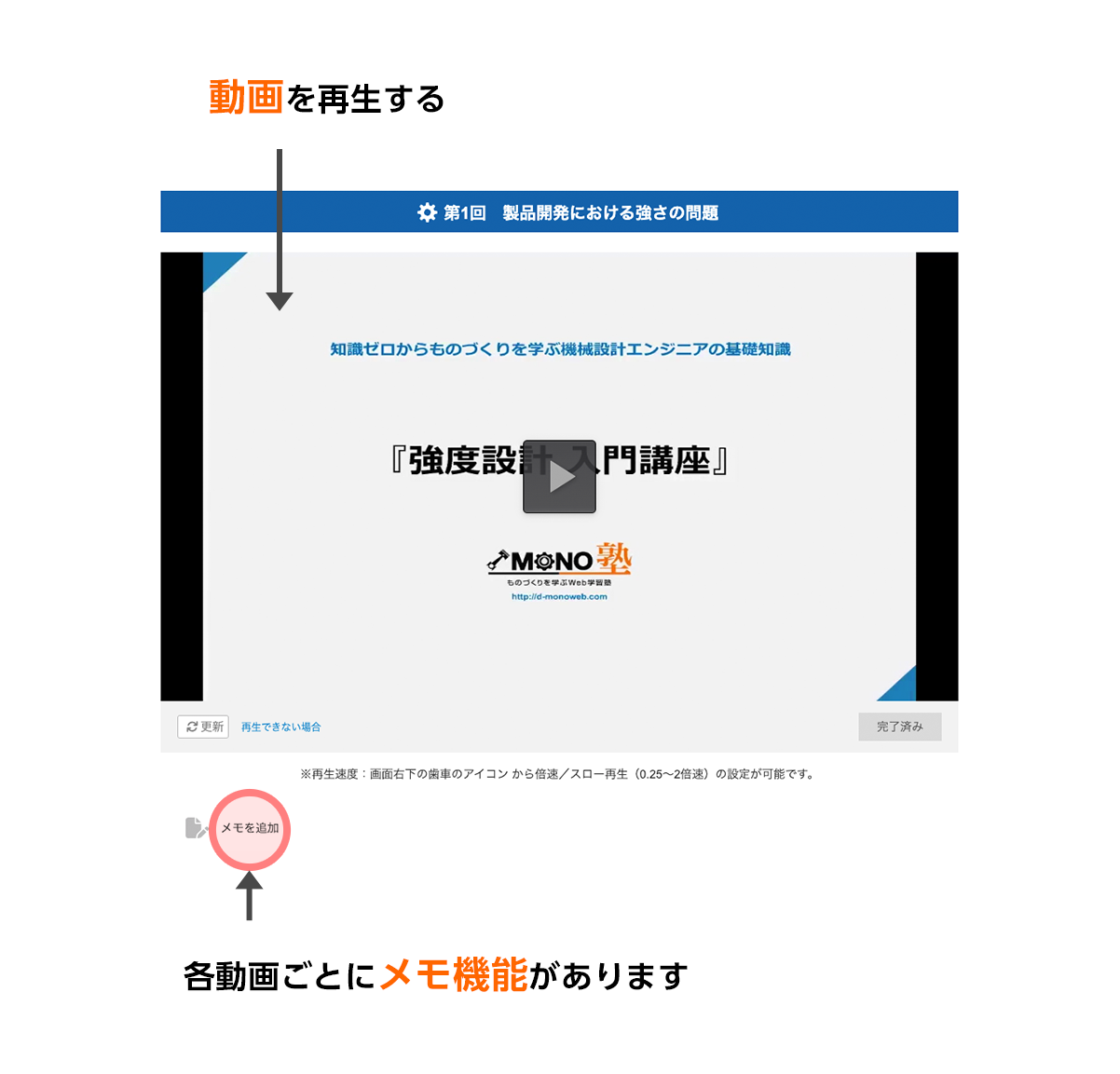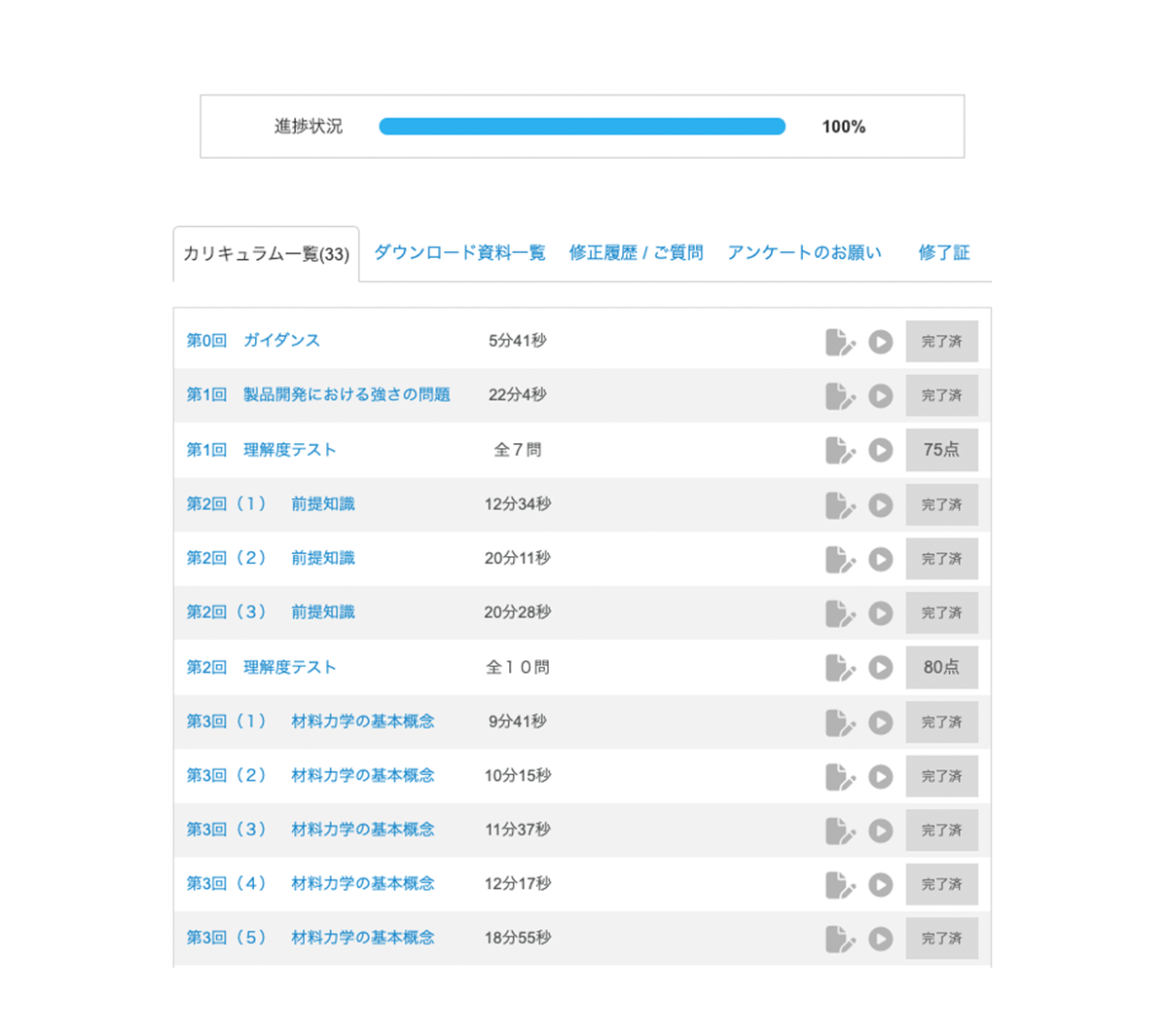

国内No.1
機械設計特化型eラーニング
eラーニング利用実績
![]()
取引企業総数
739社
上記の中で137社が
東証上場企業
![]()
eラーニング受講者延数
16,799人
当社調べ。2016年4月〜
2025年3月の間の登録数
- 自動車
- 一般機械
- 精密機器
- 家電製品
- 重工業
- 半導体
- 電子機器
東証上場企業137社、他550社以上の
さまざまな業種、規模のお客様に
ご利用いただいています。

あなたは、熱力学の学習で
こんなお悩みはありませんか?


数式を理解するのが難しい…
熱力学では、微分積分や偏微分などの数学が多く使われるため、理解できない。
学んだ知識の活用法がわからない…
熱力学の理論や法則を学んでも、それを実際の機械やシステムでどう使えばいいのかがわからないことが多い。特に、熱力学の法則を実際の設計や問題解決にどう活かせば良いのかがわかりにくい。
問題解決に直面して挫折する…
実際の設計では、理論だけではなく実践的な計算が求められる。たとえば、熱交換器の効率計算や、エネルギーシステムの最適化など、具体的な問題に取り組む際に応用力が問われる。
専門用語が難しく、内容が抽象的でイメージできない…
専門用語や複雑な理論が多く、物理的な意味や数学的な表現の扱いに苦労する。とくに、エンタルピーやエントロピーといった概念がわかりにくい。
本講座では、設計に必要な
熱力学の知識を習得できます!
熱力学の第1~2法則、およびエンタルピーとエントロピーといった基本概念を、豊富な図を用いて直感的に理解できる!
現象と数式の関係が理解できることで、エネルギー管理の最適化や技術問題への応用力が身につく!
多くの演習問題に取り組むことで、理論と実践的な知識の両方を身につけることができる!

「機械設計技術者」「計算力学技術者(熱流体力学分野)」「技術士第一次試験(機械部門)」「ボイラー・タービン主任技術者」「冷凍空調技士」「エネルギー管理士(熱分野)」「原子炉主任技術者試験」などの資格取得を目指されている方にもお勧めです。
本講座は、熱力学の基礎から応用までの知識を身につけ、
実際の工学問題への適用能力を高めることができます
- 第1章熱力学の概要
- 第2章熱力学の下準備
- 第3章熱力学の第一法則
- 第4章理想気体と状態方程式
- 第5章熱力学の第二法則
- 第6章最大仕事とエクセルギ
- 第7章混合気体と実在気体
- 第8章サイクルの具体例
第1章で熱力学の基本概念とその重要性を紹介し、基礎を学びます。第2章では、熱力学の前提条件と、物理や化学や数学の基礎知識について解説し、具体的な計算への準備をします。第3章では熱力学の第一法則を詳しく解析し、エネルギー保存の原則を掘り下げます。第4章では理想気体の性質と状態方程式を通じて、物質の状態変化について学びます。第5章で熱力学の第二法則を深く学び、エネルギー変換の限界と方向性を明らかにします。第6章では最大仕事とエクセルギの概念に焦点を当て、エネルギー利用の効率を考えます。第7章では混合気体と実在気体の挙動を分析し、理想と現実の違いを探ります。最終的に、第8章で具体的な熱サイクルの例を用いて、これまでの学びを実際のシステムに適用する方法を説明します。このカリキュラムを通じて、学習者は熱力学の基礎から応用までをしっかりと学び、実際の技術的問題を解決する能力を身につけます。
 カリキュラムの詳細は、ページ下部の説明をご確認ください。
カリキュラムの詳細は、ページ下部の説明をご確認ください。
機械エンジニアにとって「熱力学」の知識は、
様々な設計課題に対応するための強力なツールとなります

熱力学を学ぶことは、料理を作るプロセスに例えることができます。料理では、異なる食材を組み合わせて、温度や調理時間を調整することで、おいしい料理を作ります。このプロセスでは、各食材の特性を理解し、それらがどのように相互作用するかを学びます。
同様に、熱力学では様々なエネルギー形態(熱、仕事、内部エネルギーなど)を「食材」と見なし、これらを適切に組み合わせて調整します。例えば、熱を加えることでエネルギーを「調理」し、システムの効率を向上させます。料理のように、熱力学でもエネルギーのバランスを取ることが重要で、適切な「調理法」を選ぶことで、システム全体のパフォーマンスを最大化できるのです。

熱力学の原理を適切に理解し応用することで、機械設計エンジニアはエネルギー変換の効率を最大化し、エネルギーロスや不要な熱の発生を防ぎます。エネルギーの流れや変換をコントロールすることは、機械の信頼性を高め、メンテナンスの負担を軽減し、機器の寿命を延ばすことに直結します。
熱を制御することで
防ぐことができる!

発電効率の低下

空調効率の低下

地球温暖化
重要な役割を果たす「熱力学」の知識
熱力学は、機械工学の基本であり、特にエネルギーの変換と効率向上において中心的な役割を果たします。たとえば、エンジンやヒーター、冷却システムの設計において、熱力学の原理は不可欠です。これらのシステムがどのように熱を効率よく仕事(エネルギー)に変換するか、仕事によって熱を移動させるか、そのプロセスを理解するためには熱力学の知識が必要です。
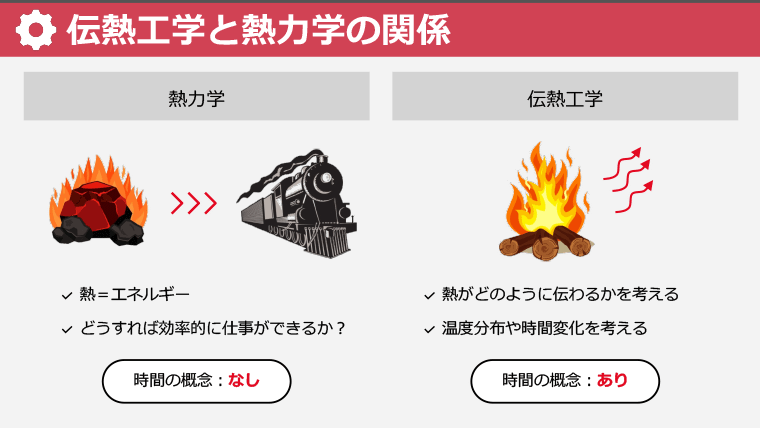
さらに、機械や電子機器の熱の流れを考える「伝熱工学」でも、熱力学の知識が基礎になります。これにより、製品設計の精度向上とエネルギー効率の最適化が可能になります。




知識不足による影響(例)
-
計算ミスが招く性能低下
熱を動力に変える過程で、計算ミスがあると、全体の性能が低下し、期待通りに動作しなくなることがあります。
-
熱サイクルの理解不足が招く課題
熱サイクルの理解が不足すると、エネルギー効率の最適化が難しくなり、燃費の悪化や運転コストの増加を引き起こす可能性があります。
-
冷却設計のミスによる過熱のリスク
熱力学の知識が不足していると、適切な冷却システムを設計できず、機械が過熱する可能性があります。これにより、性能が落ちたり故障したりする原因になることがあります。
熱力学の知識を「実際の設計現場」で活用するには?
学校では熱力学の基本的な理論を学びますが、実際の設計現場ではその理論を応用することが必要です。理論はシンプルな条件下で成り立つことが多いですが、現場では多くの変数や予測できない状況が絡み合います。
たとえば、エネルギー効率や熱の管理において、実際の設計では理論通りにいかない複雑な要素が絡み、これをうまく解決するための応用力が求められます。現場で直面する具体的な課題に対して、理論を実践的に使いこなすことが重要です。

MONO塾では、3ステップを踏むことで
熱力学の「実践的な知識」を身につけることができます。
STEP1
基本的な概念と理論の理解
まずは「熱力学の基本概念」から始め、エネルギー保存の法則、状態方程式、理想気体など重要な理論を学びます。この段階では、熱と仕事の関係やエネルギー変換の基本を理解することを目指します。
STEP2
理論から実践へ
熱交換器の設計、エネルギー効率の最適化、熱サイクルの分析など、具体的な問題に理論をどのように適用するかを学びます。実際の設計課題に理論を使うことで、より実践的な理解を深めます。
STEP3
実践力向上のための「演習」にチャレンジ
演習を通じて、学んだ理論を実際の設計課題にどう活かすかを学びます。設計現場で直面するさまざまな問題に対応し、効果的な解決策を見つける力を養います。


なぜ、MONO塾のEラーニングでは
初心者でも「基礎から実践レベルまで」
熱力学の知識が身につくのか?


理由1豊富なイラストを活用して、数式の意味をわかりやすく理解
熱力学は他の力学分野と比較して抽象的で、理解が難しいとされます。この分野では、直接観測が困難な熱エネルギーやエントロピーなどの概念を扱い、エネルギーの法則を用いて説明します。機械設計エンジニアにとって、これらの理論は高効率なシステム設計に不可欠です。
熱力学では、目に見えない現象を様々な理論を使って学びますが、一般的な教材ではいきなり複雑な数式から入るため、途中で挫折する人も少なくありません。
理由2難しい理論も身近な具体例で学べる
本講座では、難しい理論も身近な具体例を使ってわかりやすく説明しています。これにより、複雑な数式を直感的に理解し、初心者でも安心して学習を進められます。


<身近な事例を用いた説明>
※講座内の一部を紹介しています
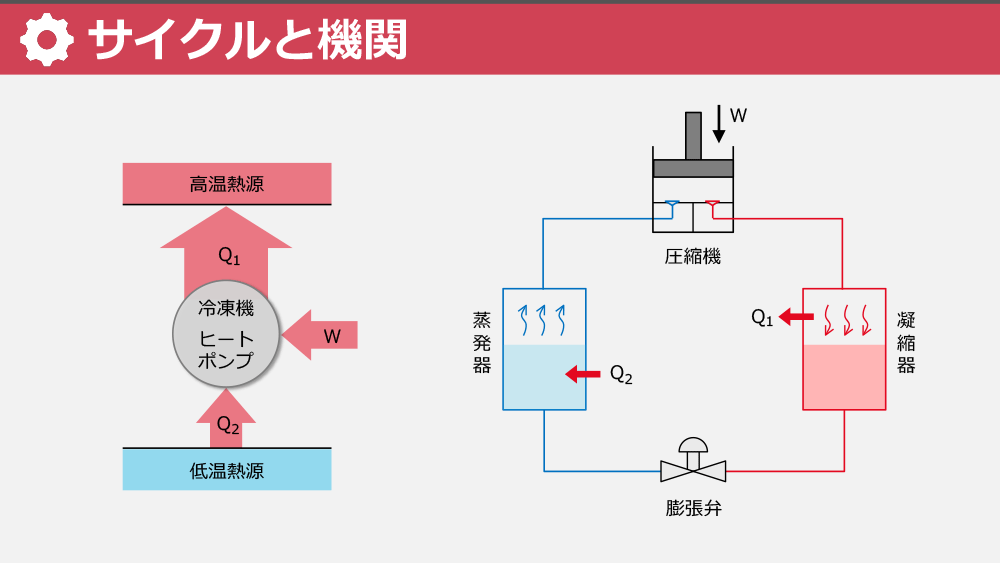
サイクルを「エアコン」を例に理解する
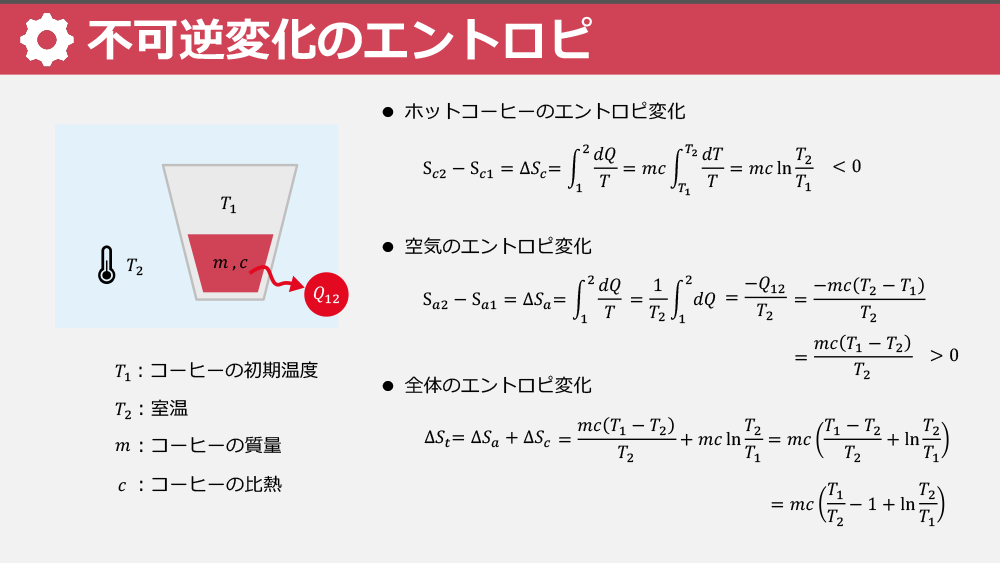
エントロピを「コーヒーとミルク」を例に理解する
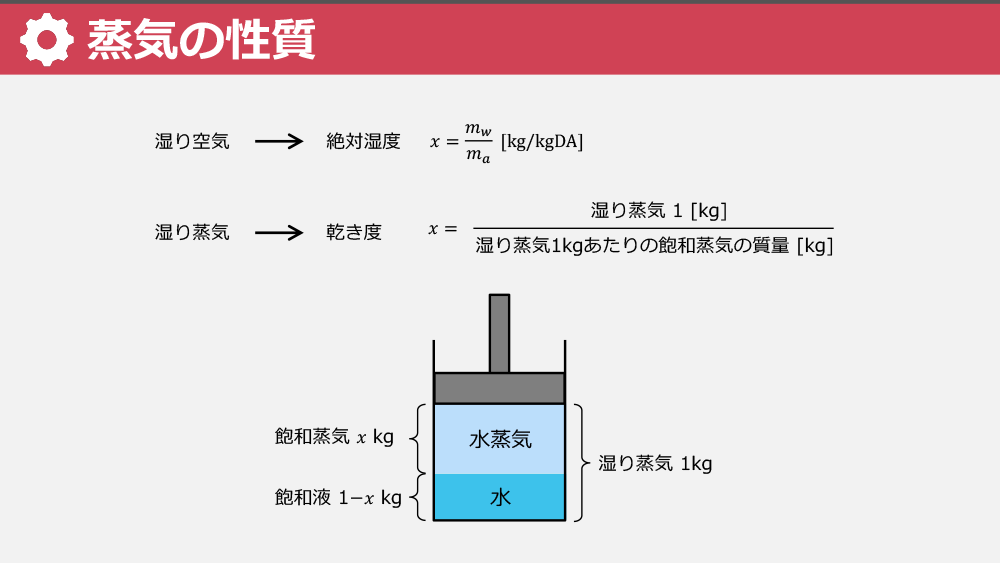
蒸気の性質を「水蒸気」を例に理解する
専門書

難しい数式ばかりで理解できない。。
本教材
数式の意味と目的もわかりやすく解説されているので、理解しやすい!
理由3実際の設計でよくある課題を演習で学べる
本講座では、基本的な解決手法だけでなく、実際の設計でよくある課題に基づいた演習を通じて理解を深めます。これにより、複雑な数式の展開ではなく、設計現場で役立つ実践力を身につけます。


<事例の紹介>
※講座内の一部を紹介しています
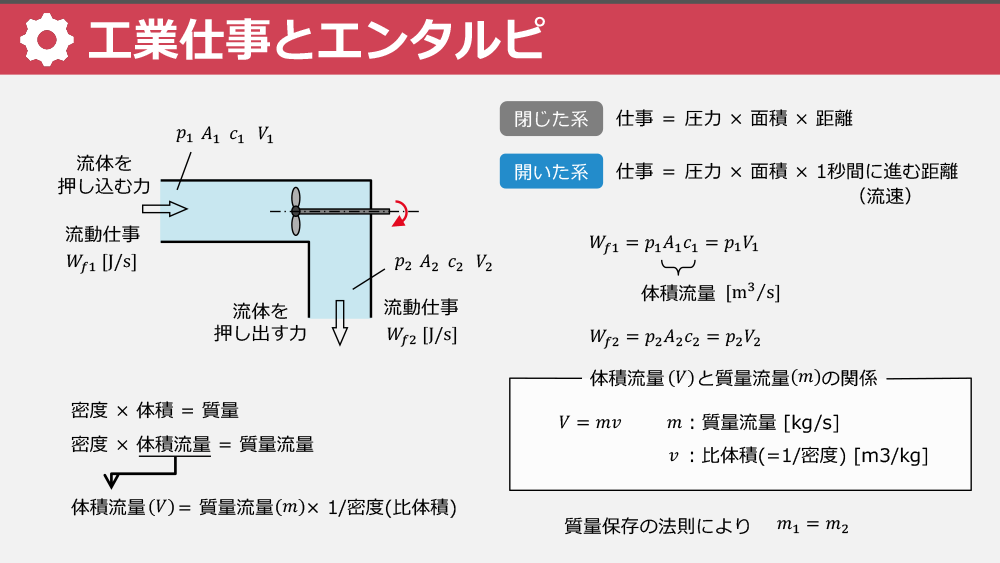
タービンを例にして、開いた系の「熱力学の第一法則」を活用し、エネルギーがどのように変換されるかを学びます。

4サイクルエンジンを例にして、「実際のサイクルと理想サイクルの違い」を学びます。エンジンの基本的な吸気、圧縮、膨張、排気の各行程を通じて、理論と現実の違いを理解できます。
<演習問題>
※講座内の一部を紹介しています
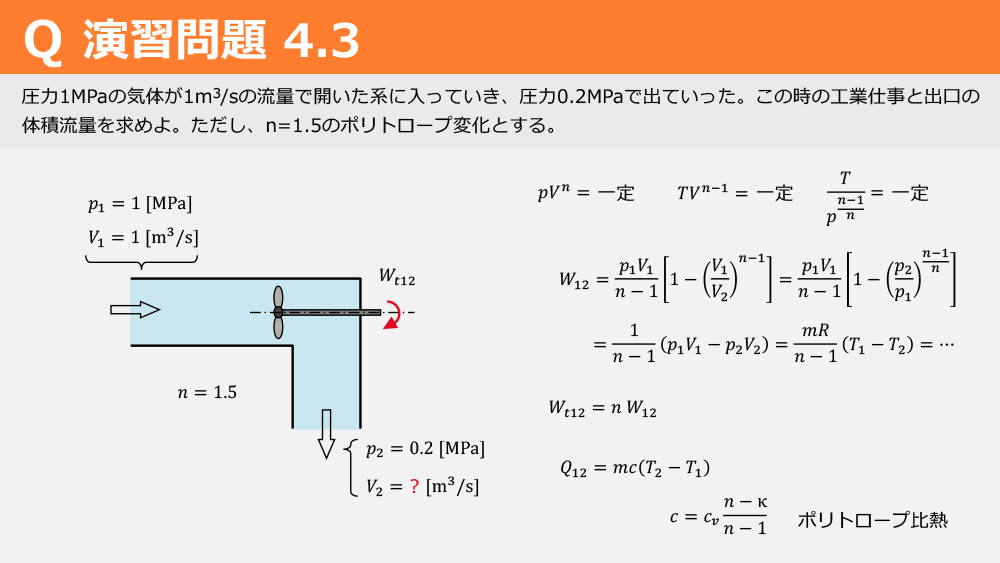
圧力差が存在する開いた系で気体が流入し、異なる圧力で流出する場合に、ポリトロープ変化(n=1.5)を適用して「工業仕事」と「出口の体積流量」を計算します。
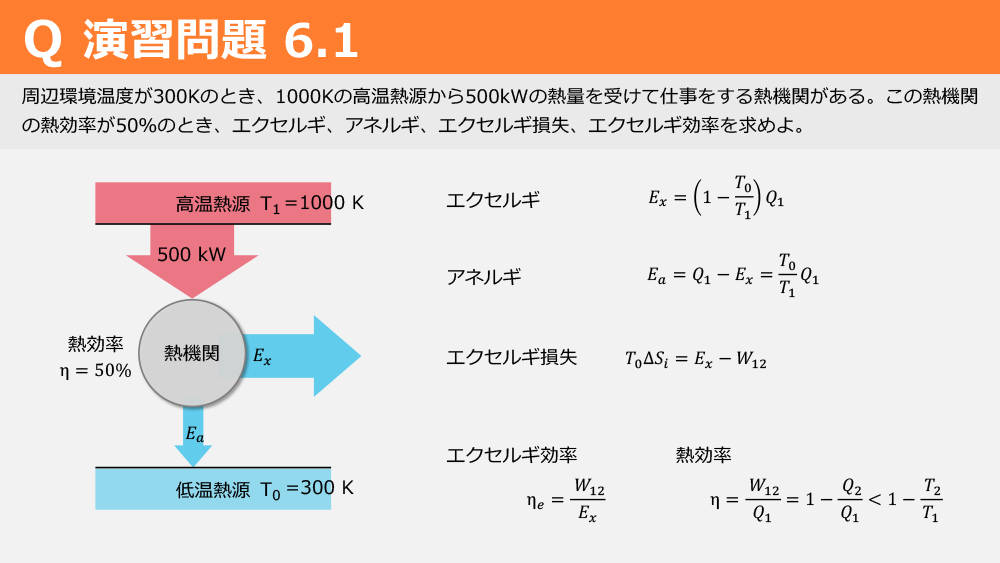
周辺環境温度が低い場合に、高温熱源から受ける熱量を利用する熱機関のエクセルギー効率を求めます。熱効率が既知である状況で、特定の外気温と熱源の温度を基準に「エクセルギー効率の計算と最適化」を行います。
専門書
機械系エンジニアに向けた事例が少ない。

本教材
豊富な事例と演習で、実践的な能力が効率的に身につく!


「MONO塾オリジナルのテスト・演習問題」で、
熱力学の知識を定着させる
MONO塾では、基本知識はもちろん、実際の設計でどう使うかなど、
ただ用語や公式を暗記するのではなく、基本知識が設計の中でどのように活用されるのか
といった【考える力】が本講座で身につきます。
MONO塾の豊富な
アウトプット!
-
1.演習問題
各章の中で用意された「演習問題」を解きます。
図解でわかりやすく解説されているため、理解を深められます。 -
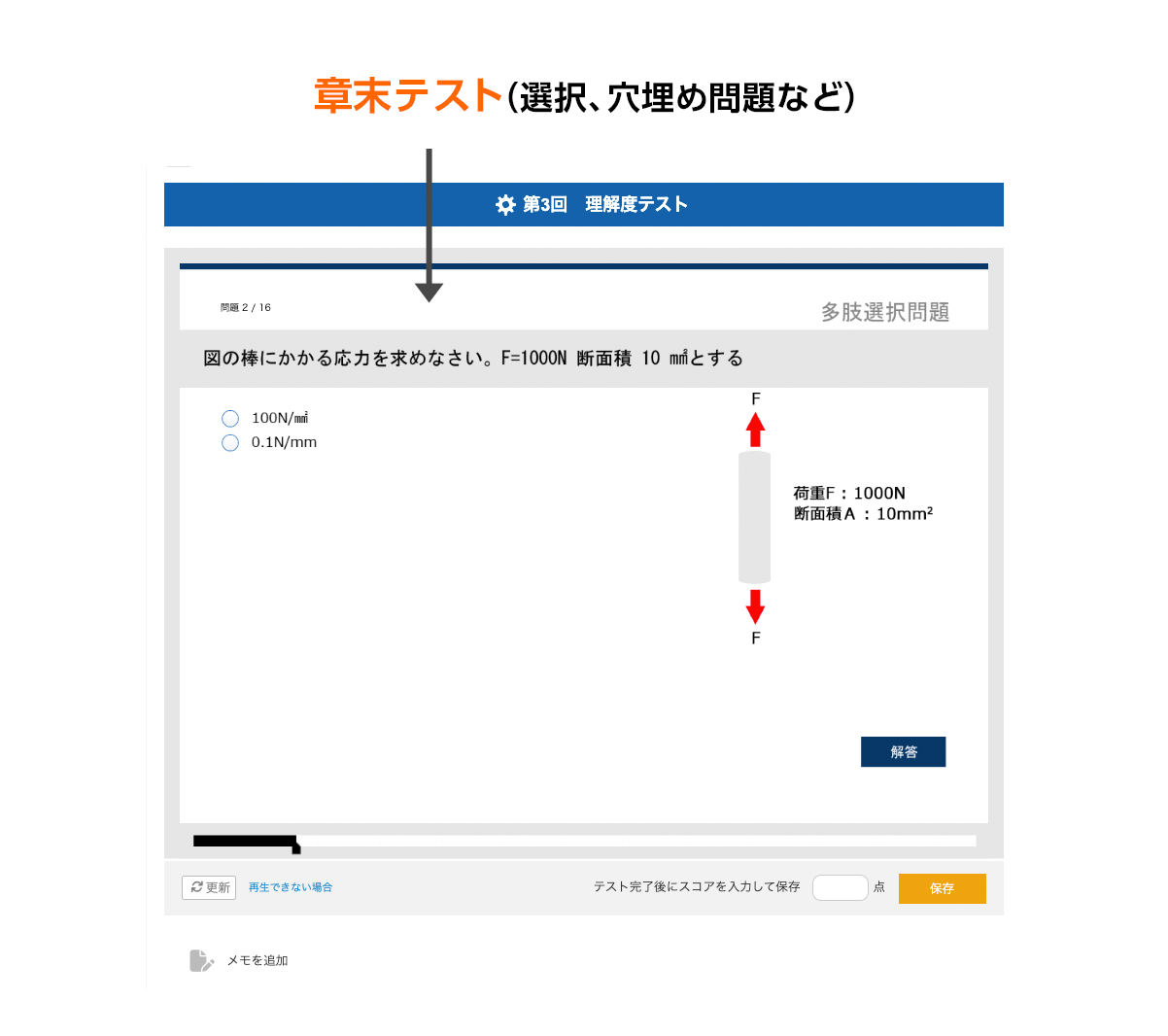
2.章末テスト
各章の最後に「穴埋め問題、◯×問題」などのテストを受けます。
学んだ内容について、理解度を確認できます。 -
3.理解度確認テスト(全50問)
講座全体の理解度を測るための「最終テスト」になります。

熱力学入門講座の
カリキュラムをチェックする
第1章
熱力学の概要
熱エネルギーの生成と伝達の原理を学び、物質の状態変化やエネルギー効率を理解する
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・本講座の全体像と学習の流れを理解する
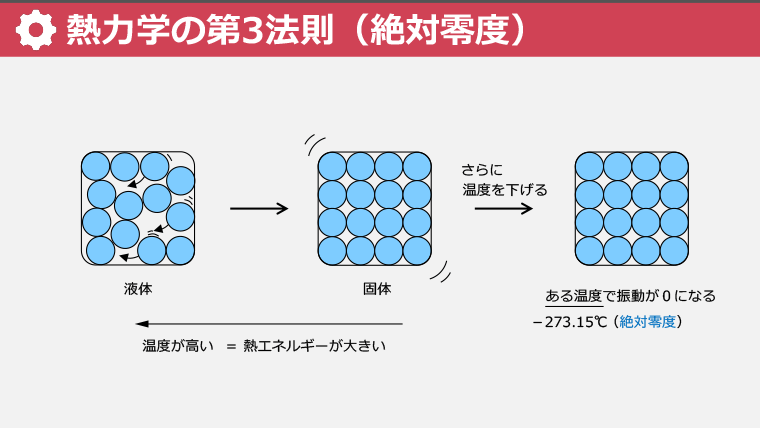
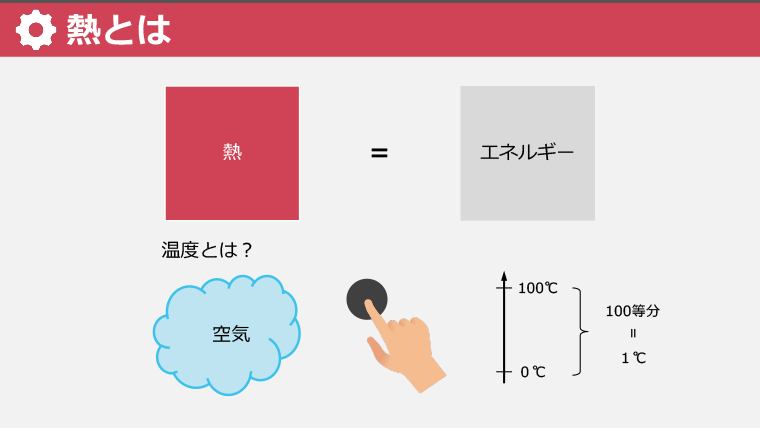
・熱とは見えないエネルギーの一形態であり、分子運動によって生じる
・熱エネルギーは分子の振動によって発生し、水の微振動からその現象を理解することができる
・絶対零度は分子の振動が完全に停止する温度で、0ケルビン(-273.15℃)に設定されている
・熱エネルギーを利用して機械を動かす原理を学び、熱の利用可能性を考える
・分子の動きは非常に複雑であり、熱力学ではこれらの集団的な動きを総合的に解析する
・温度は分子の運動エネルギーの平均値であり、このエネルギーの変化が物質の状態変化を引き起こす
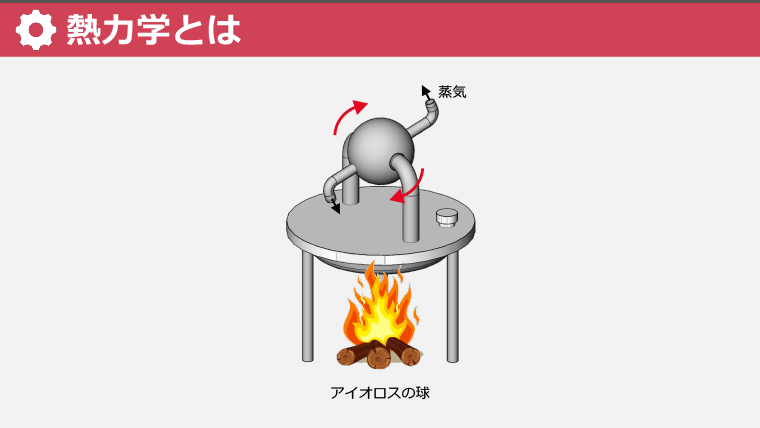
・熱力学の基礎は蒸気機関の開発に由来し、この分野の歴史はアイオロスの球から探ることができる
・熱力学が4大力学(機械力学、材料力学、流体力学)とどのように関係しているかを学ぶ
・熱力学が熱の効率的利用を学ぶのに対し、伝熱工学は熱の伝わり方を学ぶ
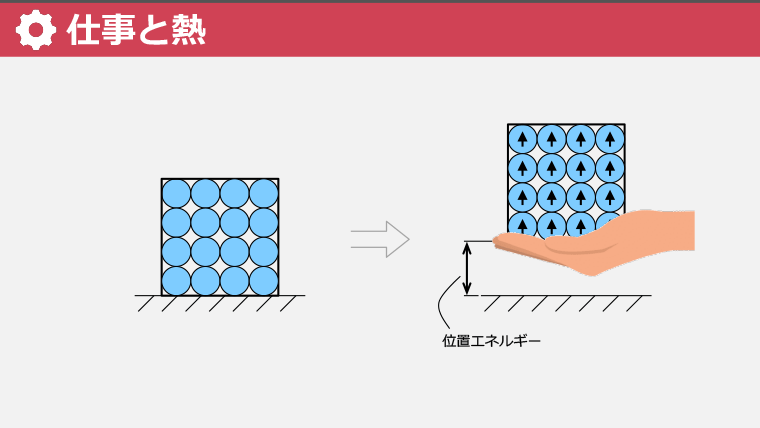
・仕事と熱はエネルギーの伝達手段であり、エネルギーの質の違いを理解することが重要である
・熱が加わると分子の運動エネルギーが増加し、それに伴い温度が上昇する
〈理解が深まる専門用語〉
熱 熱力学 温度 熱エネルギー 分子運動 絶対零度 ケルビン 質点の運動 圧力 蒸気機関 運動エネルギー 位置エネルギー 熱工学 伝熱工学 熱伝導 熱伝達 熱放射 対流熱伝達
第2章
熱力学の下準備
熱を仕事やエネルギーに変換する方法と、その背後にある物理的な原理を学ぶ
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・熱力学を理解するためには、基礎的な物理、化学、数学の知識が必須である
・熱力学で扱う対象を「系」、それ以外を「周囲」または「外界」と呼ぶ
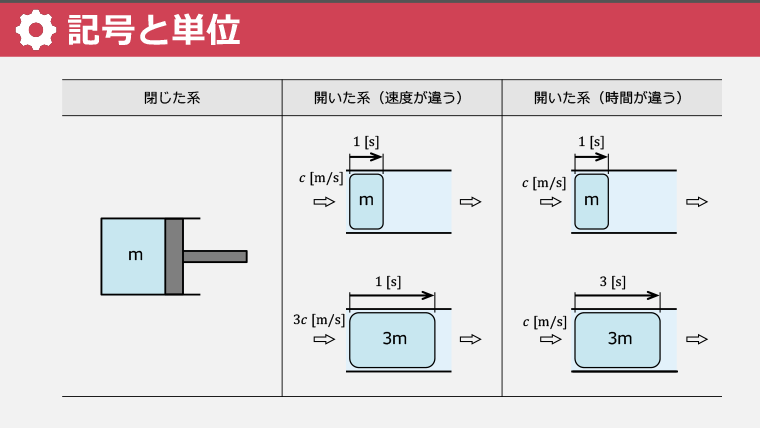
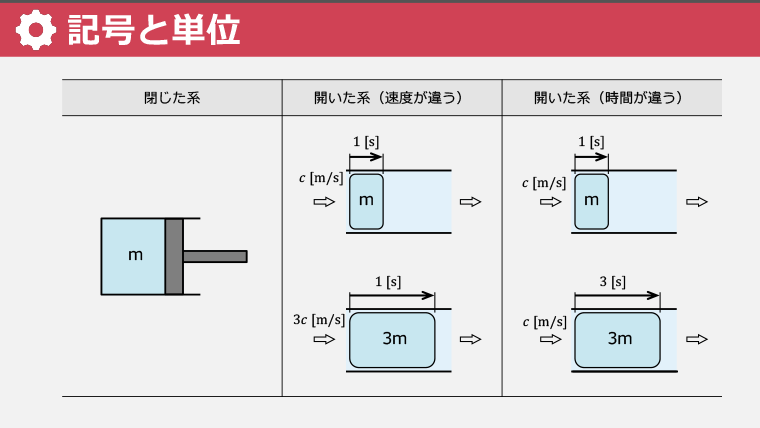
・系は「閉じた系」と「開いた系」に大きく分けられる
・閉じた系は物質の出入りがない系である
・独立系は物質やエネルギーの交換がない独立した系である
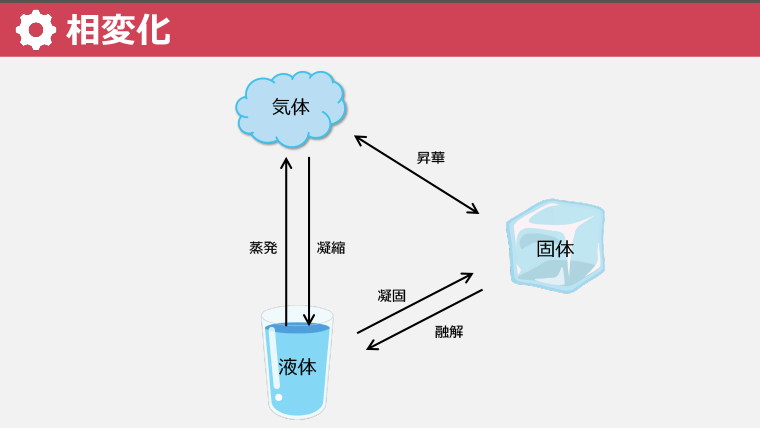
・相変化には融解、凝固、蒸発、凝縮、昇華が含まれる
・熱力学には、第0法則から第3法則までの4つの法則がある
・熱エネルギーは分子の振動によって生じ、その平均値が温度となる
・熱力学では、摂氏温度ではなく絶対温度(ケルビン)を用いる
・気体の状態は分子数によって変わり、その数はアボガドロ数を基準に計算する
・アボガドロの法則によると、等しい体積の異なる気体は同じ数の分子を含む
・化学熱力学ではモルを基本単位とし、分子量と質量の関係を学ぶ
・熱力学で扱う物理量は特定の記号で表され、温度と圧力は絶対値で扱う
・絶対圧力は絶対真空を基準として用いられる
・気体の物理量は状態量と非状態量に分けられる
・熱力学で使う状態量には温度、圧力、体積、内部エネルギー、エンタルピー、エントロピーがある
・状態量は示強性と示量性に分類される
・状態量の計算は初期と最終の状態を比較して行う
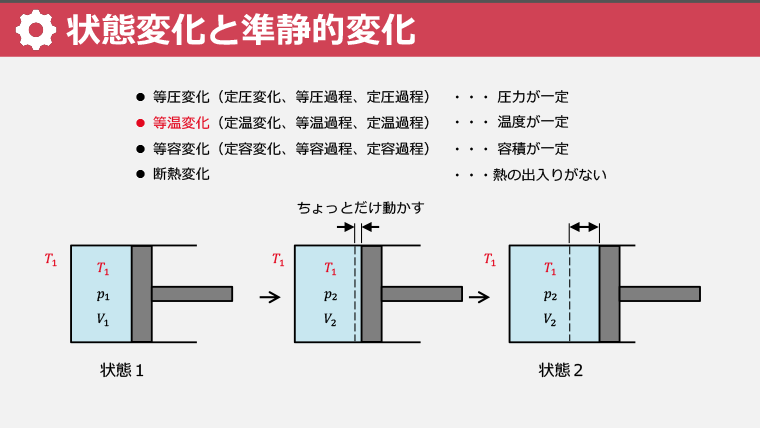
・熱力学の基本的な状態変化には、等圧変化、等温変化、等容変化、断熱変化がある
・準静的変化または準静的過程とは、ほぼ静止した状態での変化を指す
・熱力学では可逆変化を基本とし、実際の変化には補正係数が適用される
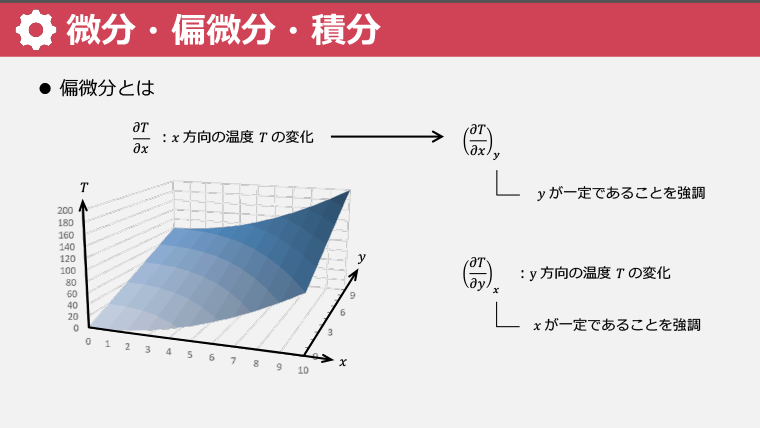
・偏微分では、全微分の公式が重要であり、変数の微小変化を偏微分で表す
〈理解が深まる専門用語〉
系 周囲 外界 境界 閉じた系 開いた系 独立系 流れ系 半閉じた系 相変化 融解 凝固 蒸発 凝縮 昇華 顕熱 潜熱 蒸発潜熱 気化熱 凝縮潜熱 熱力学の第0法則 熱力学の第3法則 熱平衡 熱力学的平衡状態 平衡状態 非平衡状態 絶対零度 エントロピー ネルンスト・プランクの定理 ケルビン セルシウス温度 摂氏温度 ヤード・ポンド法 華氏温度 アボガドロの法則 ゲージ圧力 絶対圧力 絶対真空 比体積 工業熱力学 状態量 示強性状態量 示量性状態量 非状態量 化学熱力学 状態変化 準静的変化 等圧変化 等温変化 等容変化 断熱変化 準静的過程 微分 偏微分 積分 積の微分公式
第3章
熱力学の第一法則
熱力学の第一法則を学び、エネルギー保存則やエンタルピー、絶対仕事の基本概念を理解する
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・熱力学の第一法則を学び、絶対仕事、工業仕事、内部エネルギー、エンタルピーを理解する
・第一法則は、エネルギー交換がなければ系のエネルギーは一定である
・エネルギーは仕事として外部に出力でき、外部からの仕事をエネルギーに変換できる
・熱はエネルギーの一形態で、仕事に変換したり、逆にエネルギーを熱に変換できる
・熱力学の第一法則により第一種永久機関が実現不可能なことがわかる
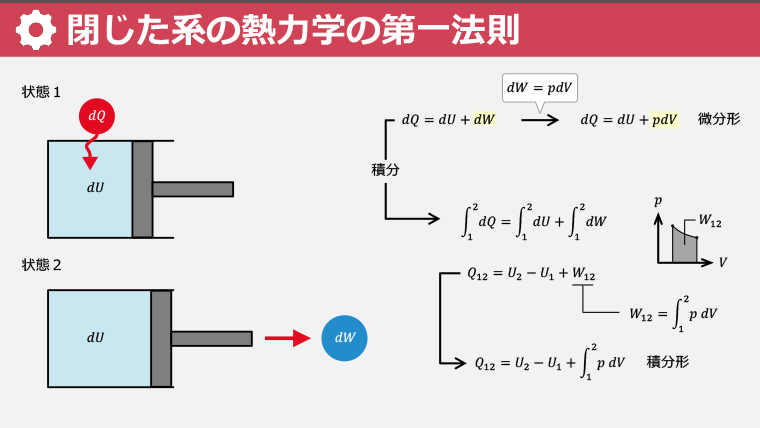
・閉じた系におけるピストンとシリンダーを使った絶対仕事の計算方法を学ぶ
・大気圧を考慮すると、絶対仕事は理論値より少なくなる
・加わる熱はエネルギー増加、行う仕事はエネルギー減少を意味する
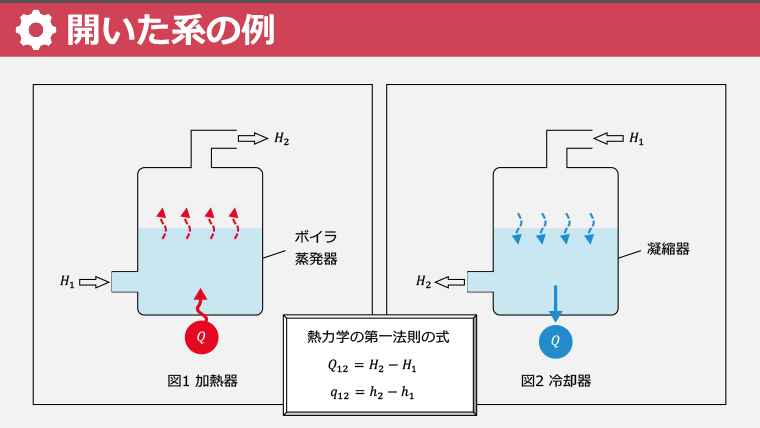
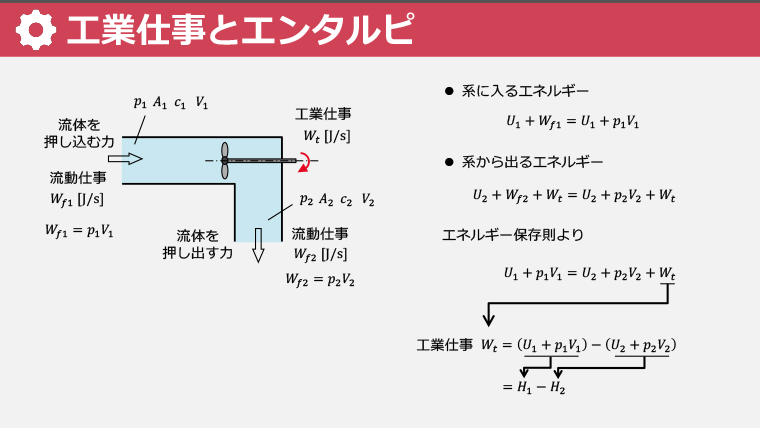
・開いた系で行う仕事は工業仕事と呼ばれ、タービンを例に学ぶ
・質量保存の法則により、開いた系では入口と出口の質量流量が等しい
・エンタルピーは内部エネルギーと圧力×体積の和である
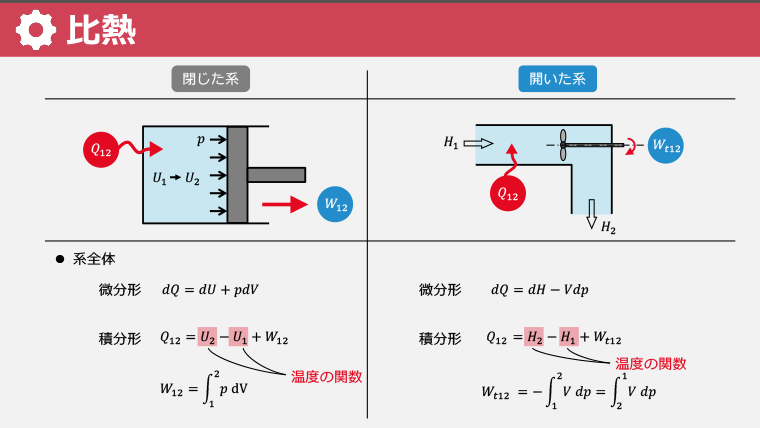
・開いた系と閉じた系を比較し、工業仕事と絶対仕事、内部エネルギーとエンタルピーの違いを学ぶ
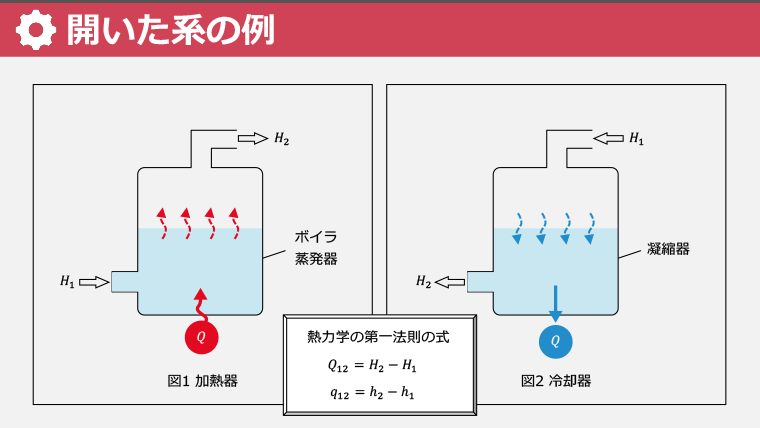
・加熱器や冷却器を例に、開いた系での熱エネルギーの処理方法を学ぶ
・工業仕事とエンタルピーの関係を、エネルギー変換プロセスを通して学ぶ
〈理解が深まる専門用語〉
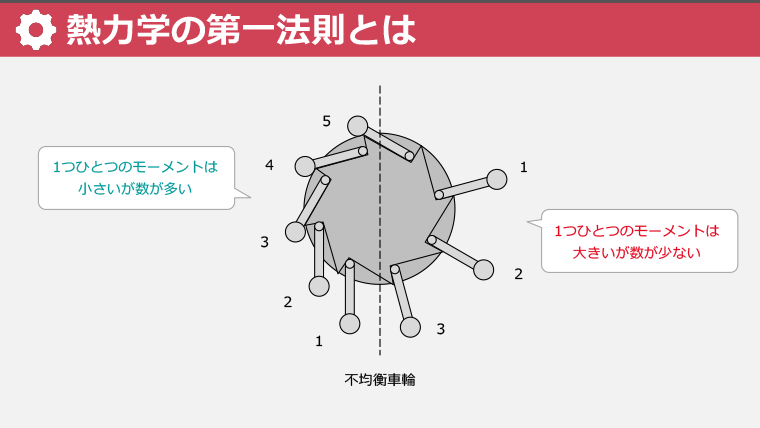
熱力学の第一法則 エネルギー保存則 ジュールの実験 蒸気機関 第一種永久機関 不均衡車輪 絶対仕事 正味の仕事 閉じた系の熱力学の第一法則 開いた系の熱力学第一法則 内部エネルギー 微分形 積分形 工業仕事 流動仕事 エンタルピー 比エンタルピー 加熱器 冷却器 熱交換器 タービン ポンプ コンプレッサー
第4章
理想気体と状態方程式
理想気体の状態方程式を基に、温度、圧力、体積の関係を理解し、熱量や仕事の計算方法を学ぶ
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・状態変化に基づいて仕事や熱量を計算し、非状態量を状態量の変化で表す方法を学ぶ
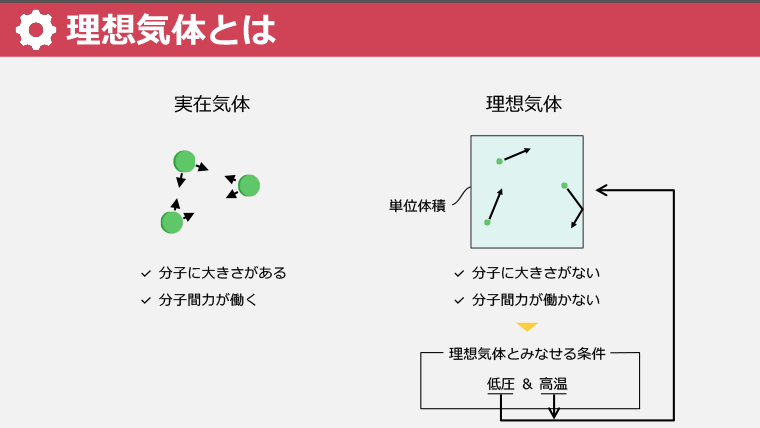
・実在気体と理想気体の違いを理解し、理想気体の概念で熱力学を簡単に解析する
・理想気体の状態方程式で圧力、体積、質量、温度の関係を理解し、ガス定数で計算する
・等圧変化の特性とボイル・シャルルの法則を理解する
・理想気体の内部エネルギーとエンタルピーは温度の関数である
・気体の比熱を、体積一定の場合と圧力一定の場合に区別し、それぞれの比熱を学ぶ
・定圧比熱が定容比熱より大きい理由を理解する
・温度、圧力、体積の関係を理解し、熱量や仕事の計算を行う
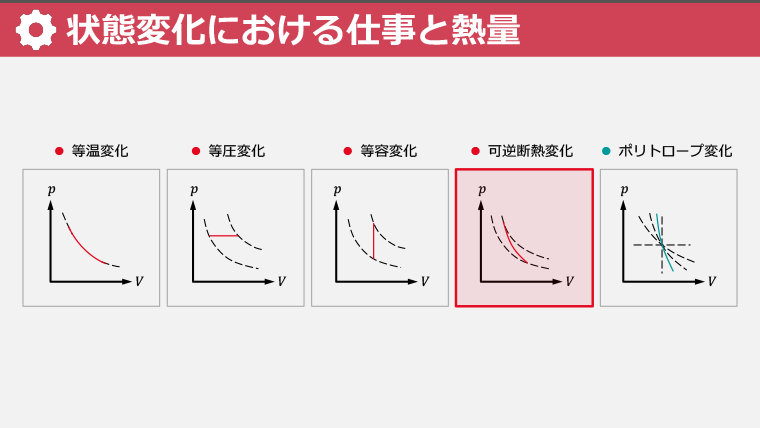
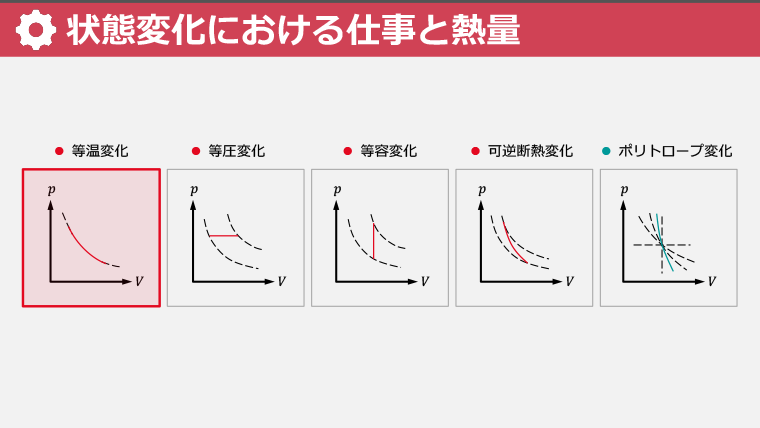
・理想気体の状態変化を等温変化、等圧変化、等容変化、可逆断熱変化で表す方法を学ぶ
・等温変化では、熱量がすべて仕事に変わることを理解する
・閉じた系での等温変化を数値で計算する方法を学ぶ
・等圧変化と等容変化の違いを理解する
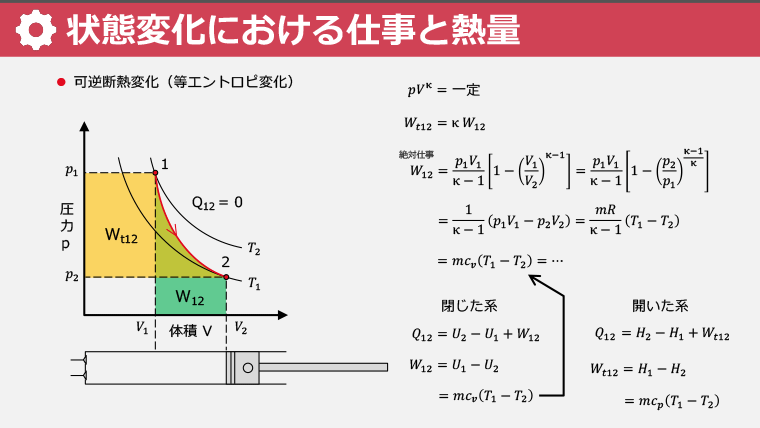
・断熱変化と可逆断熱変化(等エントロピー変化)の違いを理解する
・閉じた系の第一法則で、断熱変化が内部エネルギーの差で表されることを学ぶ
・開いた系の第一法則で、工業仕事がエンタルピーの差で表されることを理解する
・状態方程式を使い、仕事と熱量の違いを計算する方法を習得する
・実際の機械で完全な断熱が難しいことを理解し、ポリトロープ変化について学ぶ
・可逆断熱変化が理論上可能でも、摩擦や渦の影響でエネルギーが戻らないことを理解する
・状態方程式を理解することで、内部エネルギーやエンタルピー、比熱の理解を深める
・具体的な状態変化を通じて、非状態量である仕事や熱量を状態量の変化で表す方法を学ぶ
〈理解が深まる専門用語〉
理想気体 実在気体 蒸気 状態方程式 ジュール 一般ガス定数 等圧変化 シャルルの法則 ボイルの法則 ボイル・シャルルの法則 内部エネルギー エンタルピー 比熱 定容比熱 定圧比熱 狭義の理想気体 半理想気体 比内部エネルギー 比エンタルピー ガス定数 単原子気体 2原子気体 等温変化 絶対仕事 工業仕事 熱量 等容変化 可逆断熱変化 断熱変化 等エントロピー変化 微分形 ポリトロープ変化 ポリトロープ指数 不可逆断熱変化
第5章
熱力学の第二法則
熱力学の第二法則を学び、エネルギーが高温から低温へと移動する自然の法則を理解する
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・熱力学の第二法則を学び、エネルギーが高い質から低い質へと変化する法則を理解する
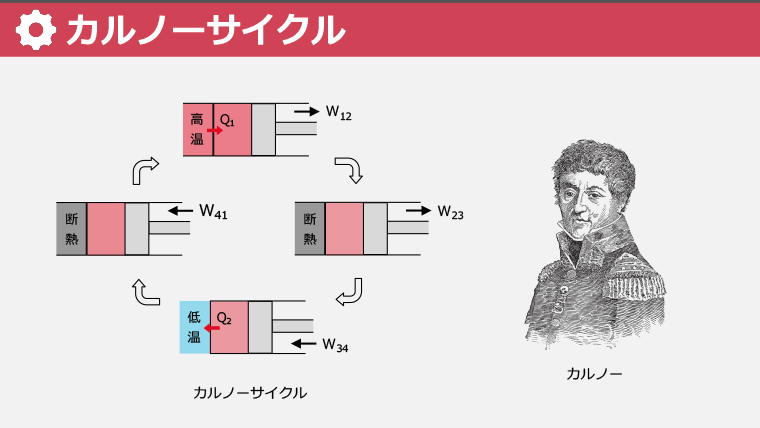
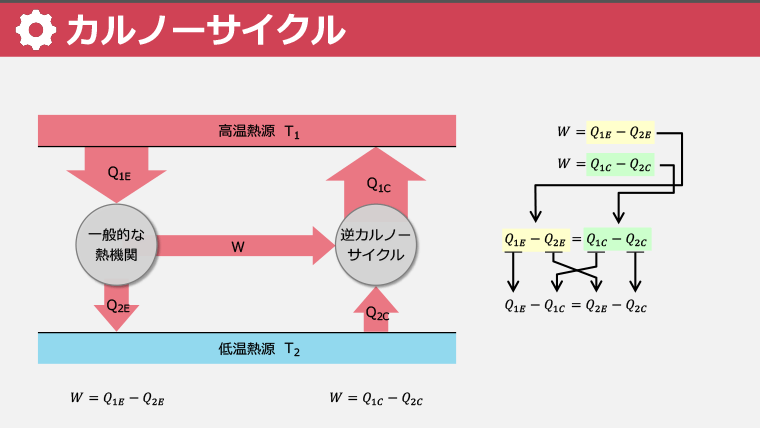
・カルノーサイクルの効率とエントロピーの概念を学び、エネルギーの一方向の流れを数値化する
・熱を仕事に変換する際の限界とその理由を、第二法則を通じて理解する
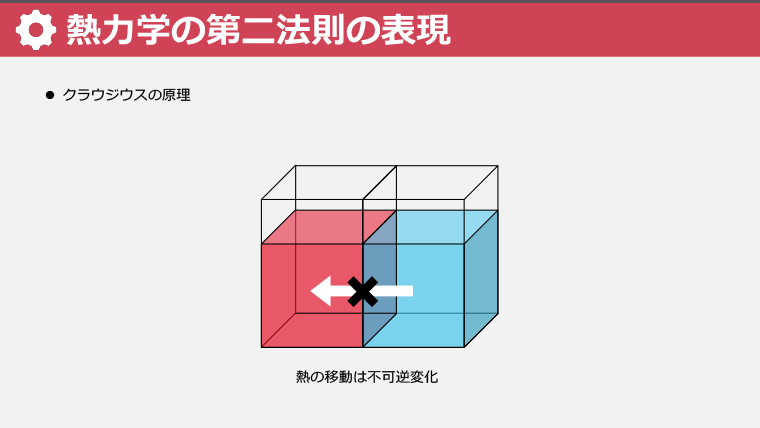
・クラウジウスの原理を学び、熱が自然に高温から低温に移動することを理解する
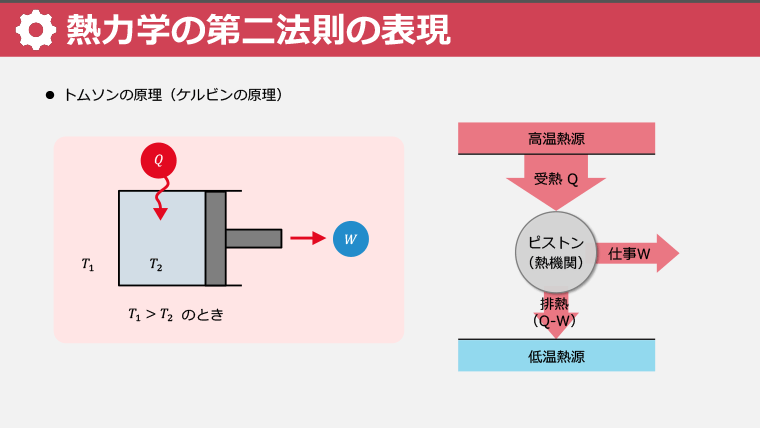
・トムソンの原理から、温度差がないと熱から仕事を得られないことを学ぶ
・熱力学の第二法則を通じて、第二種永久機関が不可能なことを理解する
・サイクルの概念を学び、エネルギー変換がサイクル内でどのように行われるかを理解する
・PV線図でサイクルの表現を理解し、実際のエンジンサイクルを例に学ぶ
・冷凍機とヒートポンプの違い、熱の移動方法を学ぶ
・カルノーサイクルは、等温膨張、断熱膨張、等温圧縮、断熱圧縮の4つの可逆変化で構成される
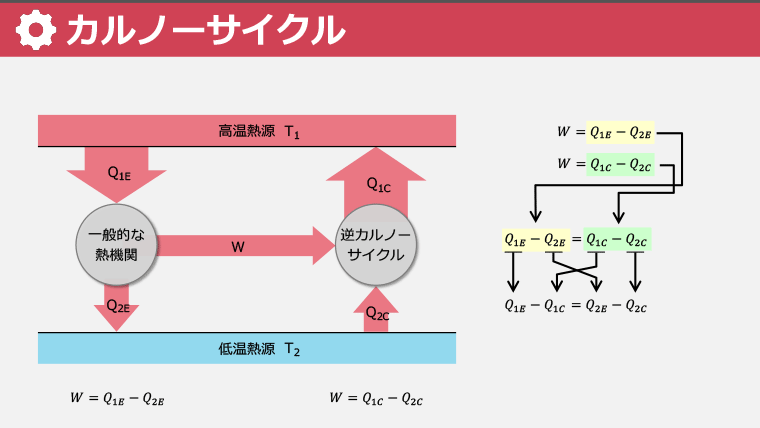
・カルノーサイクルの熱効率が最大になる理由とその計算方法を習得する
・熱効率を最適化するために、高温熱源の温度を上げるか低温熱源の温度を下げる方法を学ぶ
・カルノーサイクル以外の可逆サイクルの基本概念を理解する
・クラウジウスの積分を通じて、エントロピーの基礎を学ぶ
・エンタルピーとエントロピーの違い、それぞれの性質を学ぶ
・エントロピー増大の法則を理解し、時間の進行と不可逆性の関係を学ぶ
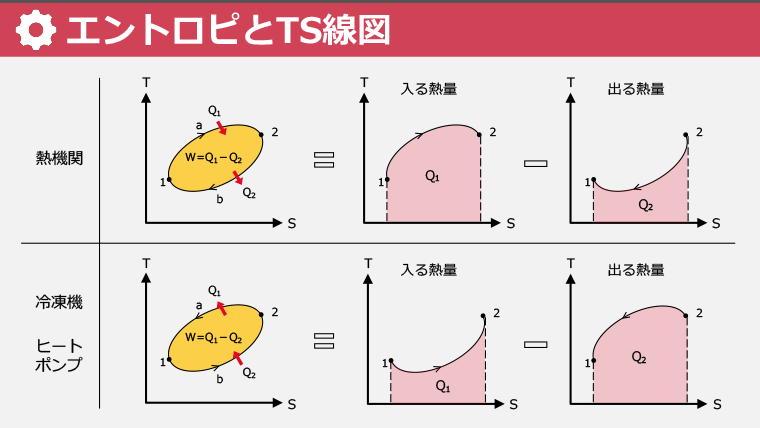
・TS線図を使った熱機関の分析方法を習得する
・温度とエントロピーの関係を理解し、可逆変化の理解を深める
・ジュールの実験を通じて、エネルギー変換がエントロピーに与える影響を学ぶ
・ホットコーヒーがなぜ自然に冷めるのかをエントロピーの変化で理解する
〈理解が深まる専門用語〉
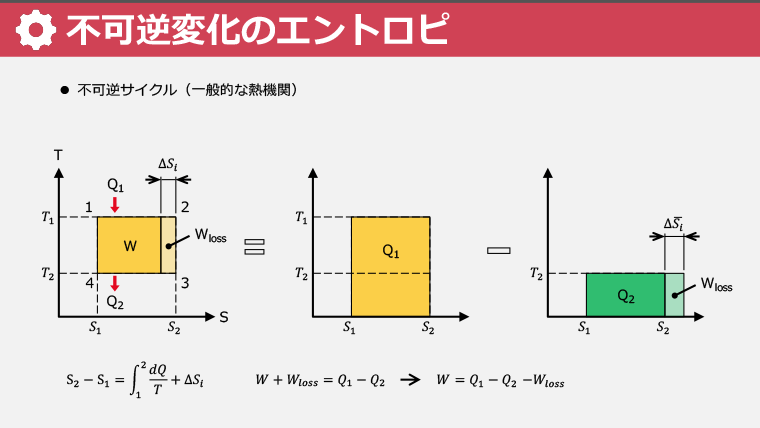
熱力学の第二法則 カルノーサイクル エントロピー トムソンの原理 ケルビンの原理 第二種永久機関 オストワルドの原理 クラウジウスの原理 対偶による証明 プランクの原理 カラテオドリの原理 サイクル PV線図 熱機関 冷凍機関 ヒートポンプ 冷媒 成績係数 等温膨張 等温変化 断熱膨張 等温圧縮 断熱圧縮 逆カルノーサイクル クラウジウスの積分 可逆サイクル 不可逆サイクル TS線図 不可逆変化のエントロピー
第6章
有効エネルギー
熱機関で受け取った熱エネルギーを、どれだけ効率的に仕事へ変換できるかを学ぶ
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・熱機関の設計において、受け取った熱エネルギーをどれだけ仕事に変換できるかを学ぶ
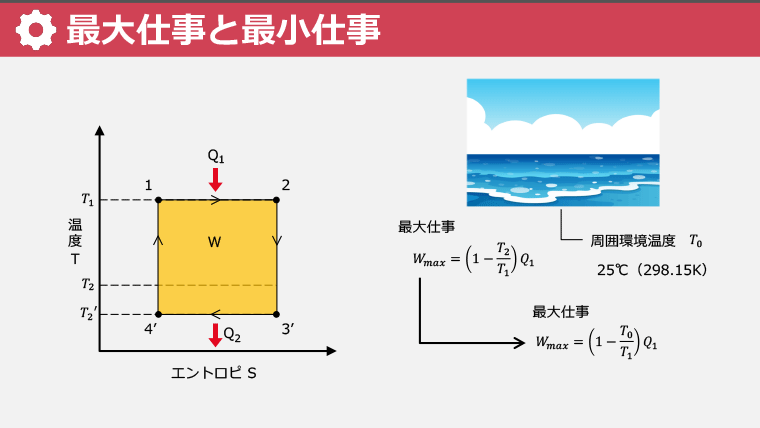
・一般的な周囲環境温度である25度(298.15ケルビン)を基に熱力学を学ぶ
・低温熱源から取り出せる最大エネルギー(有効エネルギー、エクセルギー)を理解する
・取り出せないエネルギー(無効エネルギー、アネルギー)について学ぶ
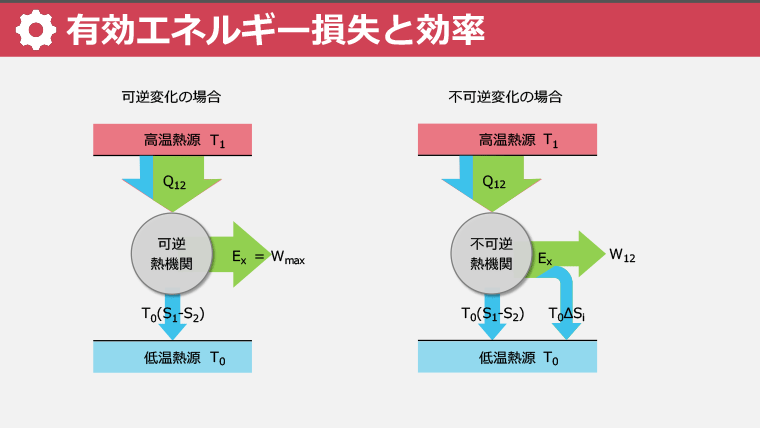
・受け取る熱量、エクセルギー、アネルギー、不可逆変化によるエネルギー損失の関係を理解する
・不可逆変化によるエントロピー増加とエクセルギー損失について学ぶ
・冷凍機とヒートポンプがどのように効率的に熱を移動させるかを理解する
・エクセルギー効率の概念とその計算方法を習得する
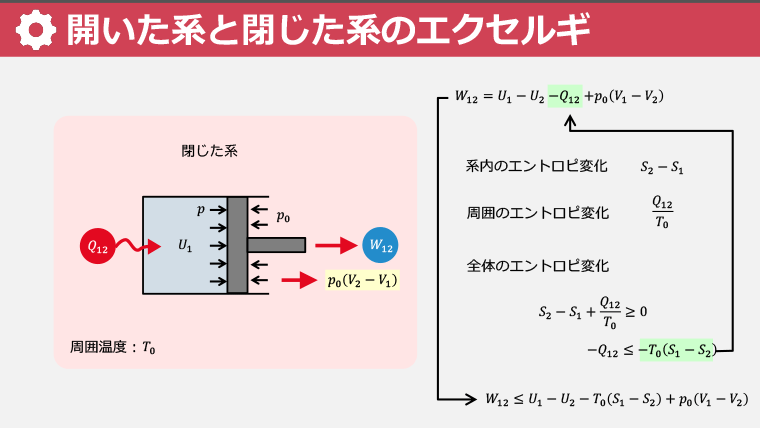
・閉じた系と開いた系におけるエクセルギーの計算方法を学ぶ
・周囲環境と同じ温度と圧力で変化した場合の、最大仕事とその計算式を理解する
・熱量や仕事が状態量ではないため、それらが状態変化によってどのように変わるかを学ぶ
・エクセルギーを使えば、変化の方法を考慮せずにエネルギー計算ができる
・変化前後のエクセルギーから、得られる最大仕事を計算する方法を学ぶ
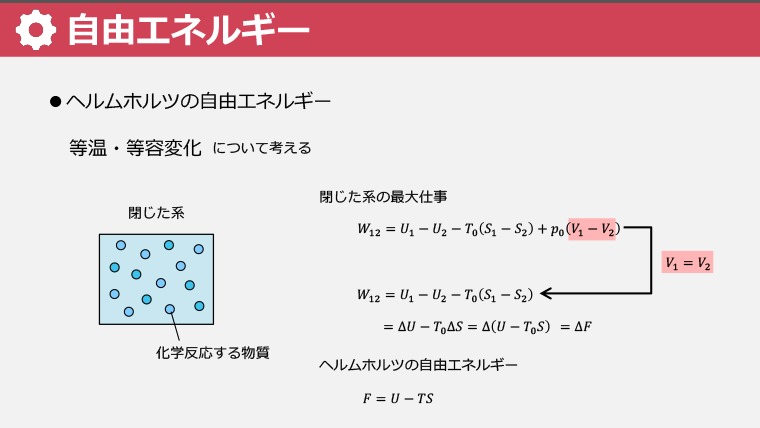
・エクセルギーと自由エネルギーの使用場面の違い(物理変化と化学変化)を学ぶ
・ヘルムホルツの自由エネルギーとギブスの自由エネルギーの違いを理解する
〈理解が深まる専門用語〉
最大仕事 最小仕事 TS線図 周囲環境温度 有効エネルギー エクセルギー 無効エネルギー アネルギー エクセルギー損失 効率 受熱量 エクセルギー効率 エントロピー エントロピー変化 自由エネルギー ヘルムホルツの自由エネルギー ギブスの自由エネルギー
第7章
混合気体と実在気体
混合気体におけるダルトンの法則や湿り空気の特性を学び、工業的な応用に必要な知識を理解する
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
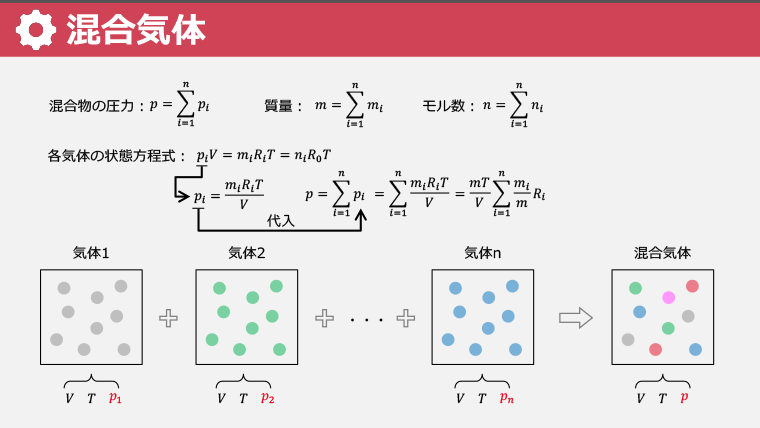
・工業で扱う混合気体の基本として、空気と水蒸気の混合気体について学ぶ
・理想気体として扱える混合気体の特徴と湿り空気について理解する
・実在気体の特性と状態方程式を学ぶ
・理想気体の混合気体に適用される「ダルトンの法則」を理解する
・混合気体中の各気体のガス定数と質量割合を使って、空気のガス定数を求める方法を学ぶ
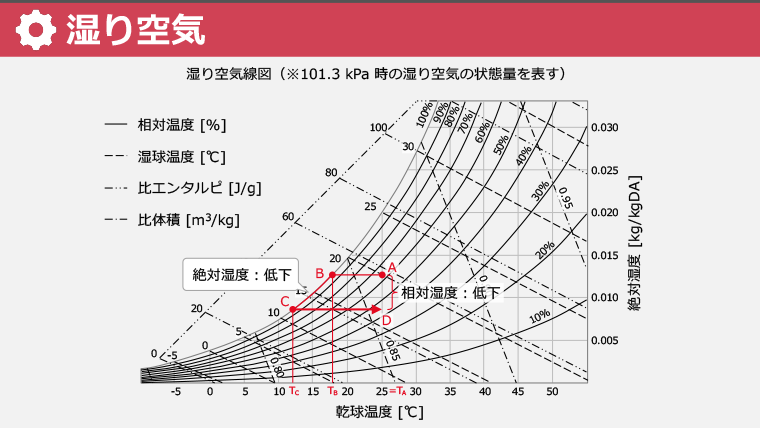
・湿り空気と乾き空気の定義を理解する
・低い分圧で水蒸気を含む湿り空気を理想気体として扱う妥当性を学ぶ
・湿り空気線図を使い、圧力に対する温度や絶対湿度などを求める方法を学ぶ
・実在気体では分子間力の影響を考慮する必要があることを学ぶ
・ファンデルワールスなどの状態方程式を学び、実在気体の挙動を解析する
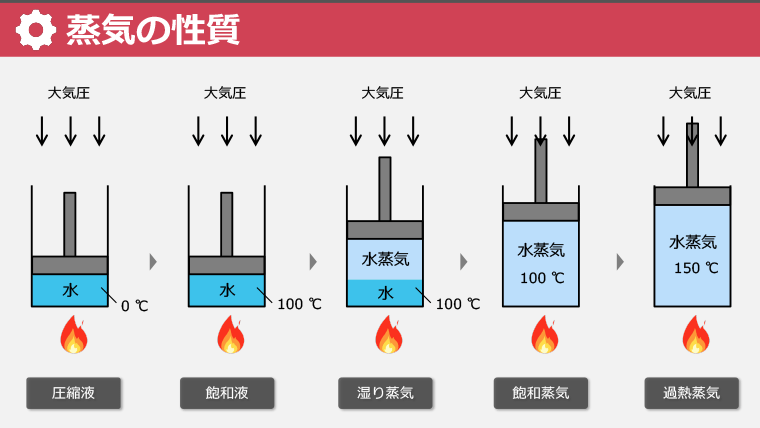
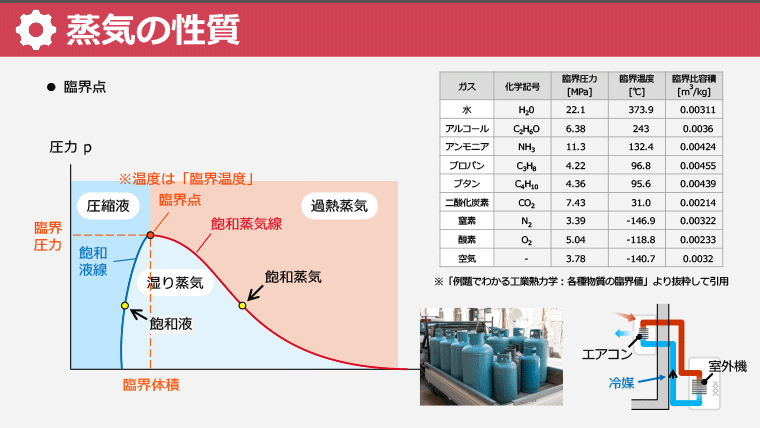
・水蒸気の性質を例に、蒸気の基本を理解する
・飽和温度に達した液体(飽和液)と沸騰前の液体(圧縮液)の違いを学ぶ
・湿り蒸気における乾き度の概念を理解する
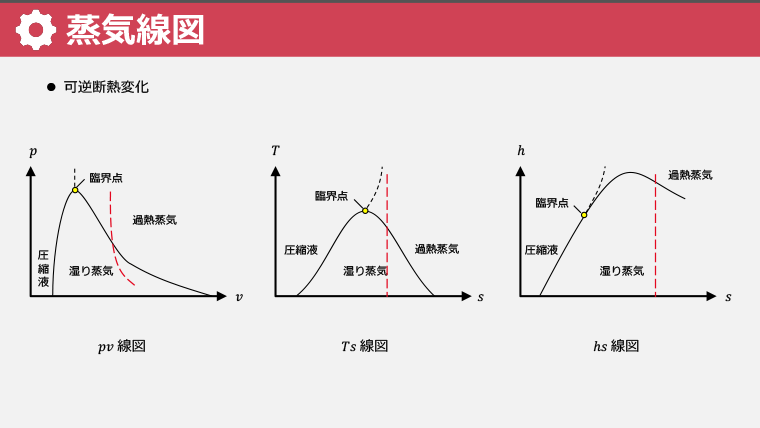
・蒸気の変化を比エンタルピーと温度のグラフで表す方法を学ぶ
・水と水蒸気が共存する状態から氷が生成する三重点を学ぶ
・水や水蒸気に関する実験データを基に、蒸気表の利用方法を学ぶ
・湿り蒸気の状態量を内挿法で求める方法を学ぶ
〈理解が深まる専門用語〉
混合気体 ダルトンの法則 ダルトンの分圧の法則 ガス定数 湿り空気 絶対湿度 相対湿度 凝縮 飽和状態 飽和空気 飽和蒸気圧力 露点温度 乾球温度 湿球温度 エンタルピ― 比体積 乾湿計 湿り空気線図 実在気体 分子間力 斥力 ファンデルワールスの状態方程式 クラウジウスの状態方程式 ビーティー・ブリッジマンの状態方程式 飽和温度 飽和圧力 飽和液 圧縮液 湿り蒸気 飽和蒸気 乾き蒸気 乾き度 過熱度 PV線図 飽和液線 飽和蒸気線 臨界点 臨界体積 臨界温度 臨界圧力 三重点 PT線図 昇華曲線 蒸気表 温度基準飽和表 圧力基準飽和表 内挿法 比容積 比エンタルピ― 比エントロピー 蒸気線図 等圧変化 等容変化 等温変化 可逆断熱変化
第8章
サイクルの具体例
熱機関のサイクル設計を通じて、連続的な仕事を取り出すための効率的なエネルギー変換の方法を学ぶ
〈eラーニングのスライド一部〉
〈学習内容を一部紹介〉
・連続して仕事を取り出すためにサイクルが必要であることを学ぶ
・実際のサイクルを紹介し、知識の活用方法を学ぶ
・熱機関をガスサイクルと蒸気サイクルに分類し、それぞれの違いを学ぶ
・スターリングエンジン(外燃機関)とガソリン、ディーゼルエンジン(内燃機関)の特徴を学ぶ
・蒸気タービンを例に、火力発電と原子力発電での蒸気サイクルを学ぶ
・カルノーサイクルや複雑な実際のサイクルの解析方法を習得する
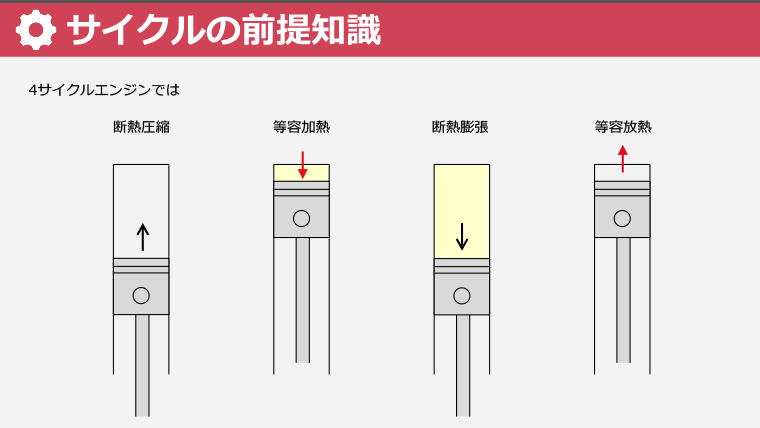
・理想サイクルの条件とその重要性を学び、4サイクルエンジンで実際のサイクルとの違いを理解する
・4サイクルエンジンの吸気、圧縮、膨張、排気の4行程を学ぶ
・ガスサイクルにはピストン式、タービン式、ジェットエンジン式があることを学ぶ
・オットーサイクルの理論熱効率と、比熱比や圧縮比が与える影響を理解する
・ガソリンエンジンとディーゼルエンジンの運動原理や燃焼方法の違いを学ぶ
・ディーゼルサイクルにおける圧縮比と締切比が熱効率に与える影響を学ぶ
・複合サイクルをPV線図やTS線図で解析する方法を学ぶ
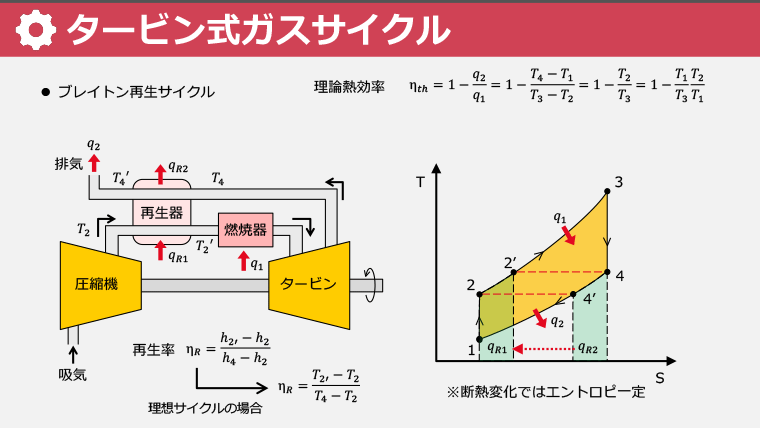
・ブレイトンサイクルとその改良サイクルを学び、等圧変化と断熱変化の関係を理解する
・ブレイトン再生サイクルでは圧力比が大きいほど熱効率が低下することを学ぶ
・ブレイトン再生サイクルの圧力比と熱効率の関係を理解し、TS線図で表す方法を学ぶ
・ランキンサイクルが蒸気タービンを使う火力発電や原子力発電の基本サイクルであることを学ぶ
・再熱ランキンサイクルで、タービンと再熱器を追加しカルノーサイクルに近づける方法を学ぶ
・混合給水加熱器型と表面給水加熱器型の加熱方法を学び、ランキンサイクルの熱効率向上を理解する
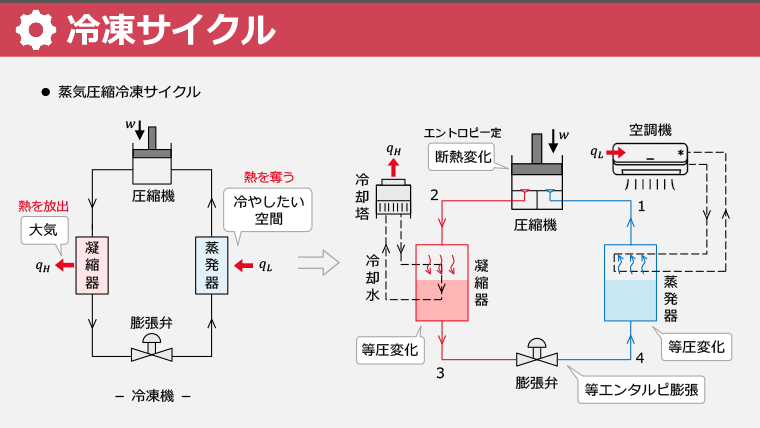
・冷凍サイクルを学び、熱を低温から高温へ移動させる原理を理解する
・蒸気圧縮、吸収式、空気冷凍サイクルの特徴を学ぶ
・蒸気圧縮冷凍サイクルの冷媒の流れと、膨張弁の機能で温度が下がる原理を理解する
・ジュール・トムソン係数による圧力変化時の温度変化と、冷媒温度を下げる条件を学ぶ
・蒸気圧縮冷凍サイクルで熱を奪う原理と成績係数の計算方法を学ぶ
・蒸気圧縮冷凍サイクルの成績係数を上げる方法を学ぶ
・化学反応を利用する吸収式冷凍サイクルの原理を理解する
・逆ブレイトンサイクルを使った空気冷凍サイクルのPV線図とTS線図を学ぶ
〈理解が深まる専門用語〉
サイクル ピストン式 スターリングエンジン ガソリンエンジン ディーゼルエンジン ガスサイクル タービン式 ガスタービン ジェットエンジン 外燃機関 内燃機関 蒸気サイクル 蒸気タービン 理想サイクル 4サイクルエンジン 上死点 下死点 閉曲線 等温変化 等圧変化 等容変化 可逆断熱変化 ポリトロープ変化 断熱圧縮 等容加熱 断熱膨張 等容放熱 正味熱効率 理論熱効率 図示熱効率 機械効率 図示仕事 受熱量 ピストン式ガスサイクル オットーサイクル ノッキング オクタン価 ディーゼルサイクル 複合サイクル ブレイトンサイクル ブレイトン再生サイクル エリクソンサイクル ランキンサイクル 再熱ランキンサイクル 再生ランキンサイクル 混合給水加熱器型 表面給水加熱器型 再熱・再生ランキンサイクル 冷凍サイクル ジュール・トムソン効果 蒸気圧縮冷凍サイクル ph線図 モリエル線図 吸収式冷凍サイクル 空気冷凍サイクル
自分のペースに合わせて
学習を進める
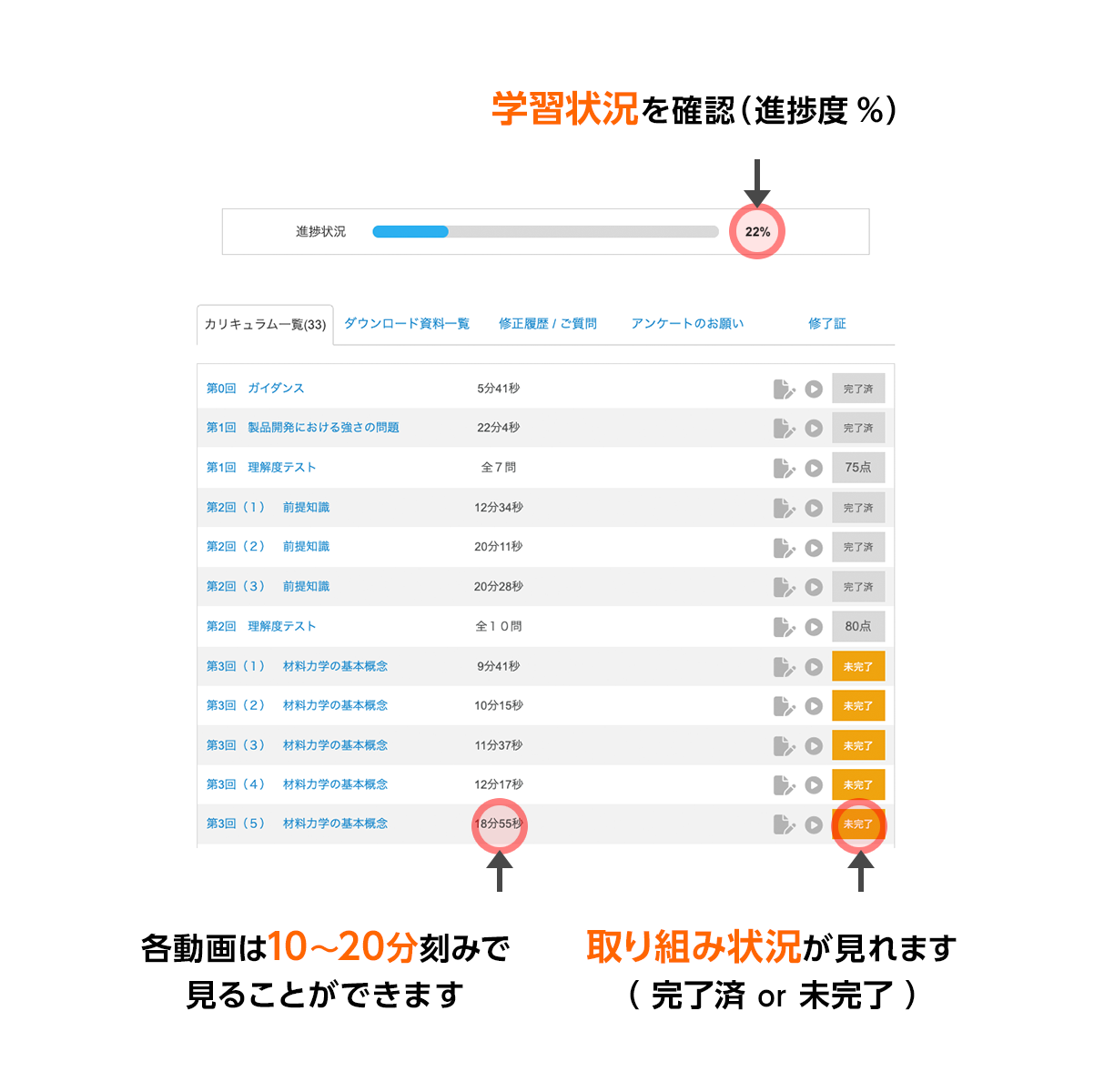
eラーニング学習のメリットは、自分のペースで学習することができることです。
「今すぐに熱力学の知識を身につけたい」という方は、1日の学習時間を集中してとることで短期間ですべてのカリキュラムを受講することができます。また「仕事をしながら自分のペースで学びたい」という方は、1日20分程度の時間から受講できますのでご自身で計画を立てながら進められます。
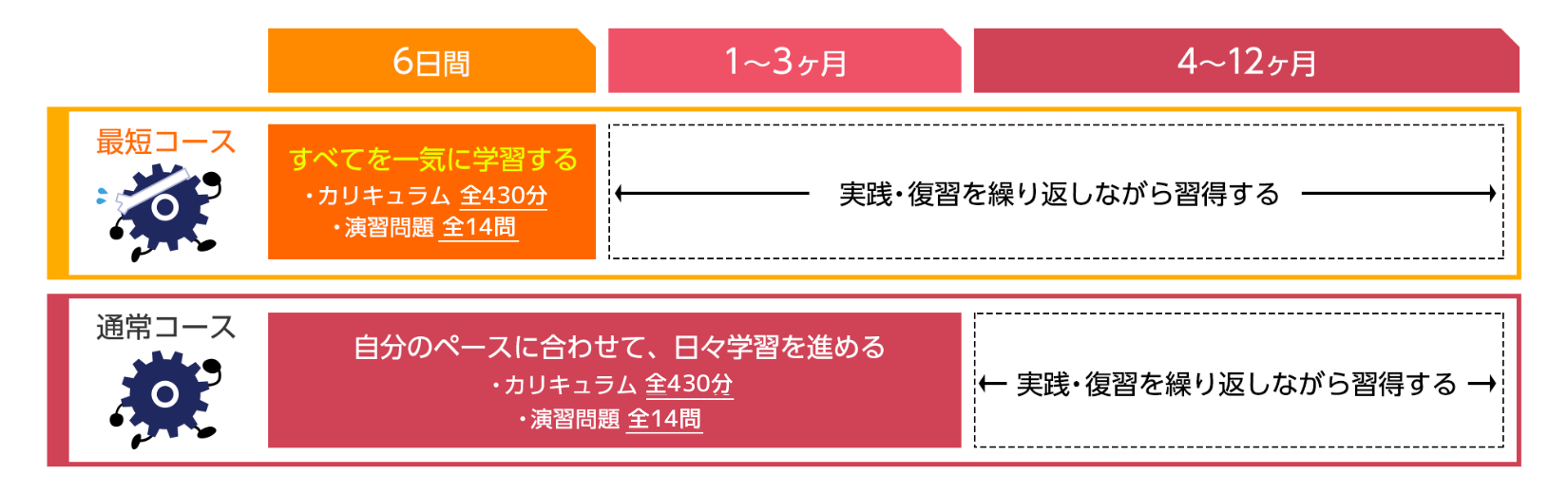
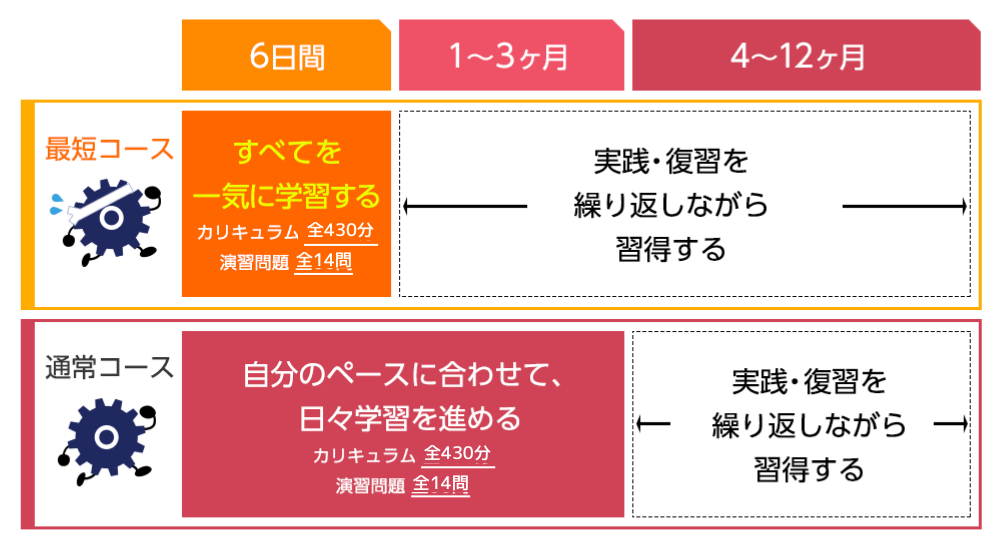
日々の学習イメージ

熱力学入門講座の概要
熱力学の基礎から応用までを習得する

定価45,000円(税込49,500円)/1アカウント
販売価格/1アカウント
7月20日(日)迄
20%OFF実施中!
再生時間430分(カリキュラム全8章分)
閲覧可能期間1年間
eラーニング以外の特典
- 特典1:熱力学入門講座テキスト(155ページ)
- 特典2:工学知識きその基礎講座 Eラーニング
支払い方法支払いは、「クレジット支払い」「銀行振込み」「コンビニ払い」をお選び頂けます。
法人でお申込みされる方へ
● 3名以上(アカウント複数申請)で法人割引(最大30%割引)をご利用頂けます。
● 希望される場合は請求書発行(PDF、郵送)をご依頼頂けます。

お求めやすい方法で購入いただけます。
分割払い月々円×6回
分割手数料なし・金利0%の6回分割となり一括払いと同額です。
一括払い一括円
今だけの限定特典!
受講者全員に“設計に役立つ
特典”をプレゼントします
特典
1
読んで学べる!書き込める!お調べ帳としても活用できる!
講座テキスト(155ページ)
本テキストは動画講座の補足用参考書としてご利用頂けます。ですので「eラーニングの復習に使いたい」「テキストにメモをしたい」という方に適しています。
eラーニング同様、図解で説明していますので初心者の方でもわかりやすい。読み進めるだけでイメージができるので理解が進んでいきます。どうぞご自宅や作業デスクなどに置いてご活用ください。
便覧や参考書、インターネットで調べなくても、テキストにわかりやすく情報がまとめられていますので「お調べ帳」としてもご活用ください。


特典
2
ビギナー設計者必見!最低限必要な基礎知識を学ぶ
工学知識きその基礎講座
Eラーニング(3,980円相当)2019/4/1に追加
「文系出身者」「転職者」「工学知識が不安なエンジニア」など、超初心者向けのEラーニングとなります。
本商品は、3,980円で単体販売も行なっています。
設計者にとって、当たり前に知っておくべき最低限必要な工学知識を習得できますので、基礎から学ぶ必要性を感じている方には役立つ学習内容です。
単位 規格 数学 力学 形状 道具
こちらの6つの基礎知識を「 0(工学知識の乏しい状態) 」から習得できます。
「設計業務の中で理解力不足を感じている・・・」
「専門知識を学習するための基礎能力が足りていない・・・」
という不安を感じている方であれば、こちらの「工学知識きその基礎講座」を学ぶことで、他専門分野の知識が学習しやすくなります。
専門知識の学習を始める前に、本講座を事前学習することをオススメします。

よくある質問
![]() グループ割引はありますか?
グループ割引はありますか?
![]() はい、ございます。同僚や友人と割引を利用したグループ購入をされる場合は「法人購入(複数人での購入)」を行ってください。グループで購入される場合も、法人割引を適応させて頂きます。その場合は、購入代表者の方に全員分のアカウントをご提出頂きます。
はい、ございます。同僚や友人と割引を利用したグループ購入をされる場合は「法人購入(複数人での購入)」を行ってください。グループで購入される場合も、法人割引を適応させて頂きます。その場合は、購入代表者の方に全員分のアカウントをご提出頂きます。
![]() 請求書の発行はできますか?
請求書の発行はできますか?
![]() はい、できます。法人で「銀行振込」を選択頂きお申込ください、マイページの「購入履歴」からダウンロードいただけます。
はい、できます。法人で「銀行振込」を選択頂きお申込ください、マイページの「購入履歴」からダウンロードいただけます。
![]() 分割での購入はできますか?
分割での購入はできますか?
![]() 個人でお申込み&クレジット支払いの方に限り、6回の分割払いができます。
個人でお申込み&クレジット支払いの方に限り、6回の分割払いができます。
![]() スマホやタブレットでも学習できますか?
スマホやタブレットでも学習できますか?
![]() はい、スマホ、タブレットでもご視聴頂けます。
はい、スマホ、タブレットでもご視聴頂けます。
サンプル動画を見てチェック頂く事をお薦め致します。